Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку Свойства равнобедренного треугольника

Содержание

Медианы, высоты и биссектрисы треугольника. Равнобедренный треугольник.
Медианы, высоты и биссектрисы треугольника. Равнобедренный треугольник. Треугольник называется равнобедренным, А В М Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется В любом треугольнике медианы пересекаются в одной точке. Медианы в треугольнике А В А Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой В любом треугольнике биссектрисы пересекаются в одной точке. Биссектрисы в треугольнике. А В Н Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную Высоты в треугольнике Существует ли равнобедренный треугольник с углами 35º, 45º? ПРАКТИЧЕСКАЯ РАБОТА Изобразите в тетради равнобедренные треугольники ( тупоугольный, остроугольный и В равнобедренном треугольнике углы при основании равны RTSQPR65˚75˚50˚120˚30˚40˚100˚45˚45˚ Найдите ошибку в решении задач ВерныйрезультатRTSQPR65˚65˚50˚120˚30˚30˚90˚45˚45˚ Физкультминутка.Упражнения для глаз. Нарисовать ими следующие геометрические фигуры:правильный треугольник;окружность по часовой стрелке, ПРАКТИЧЕСКАЯ РАБОТА Возьмите треугольник ТЕОРЕМА : Биссектриса равнобедренного треугольника является одновременно его медианой и высотой АВСК∆ АВС –равнобедренный,АС – основание, ВК – биссектриса.АС = 10 смНайти АК.DАСВDA Задача № 3АВ=АС, АD ┴ ВС < ВАD=20º, ВD=2 смНайти DС и Задача № 4АВ=АС, Домашнее заданиеГлава 3, п.2(теоремы 3,4). . 1. Я научился…2. Было трудно…3. Сегодня я узнал…4. У меня получилось…5.
Слайды презентации

Слайд 2

Слайд 3 Медианы, высоты и биссектрисы треугольника. Равнобедренный треугольник.


Медианы, высоты и биссектрисы треугольника. Равнобедренный треугольник.

Слайд 4 Треугольник называется

Треугольник называется равнобедренным,

равнобедренным,

если у него две стороны равны

АС и ВС – боковые стороны
АВ – основание
С – вершина равнобедренного треугольника

ےА и ےВ – углы при основании




B

A

C



АС = ВС





Слайд 5 А
В
М
Отрезок, соединяющий вершину треугольника с

А В М Отрезок, соединяющий вершину треугольника с серединой противоположной стороны,

серединой противоположной стороны, называется медианой треугольника.


С
СМ = МВ
Медиана

треугольника

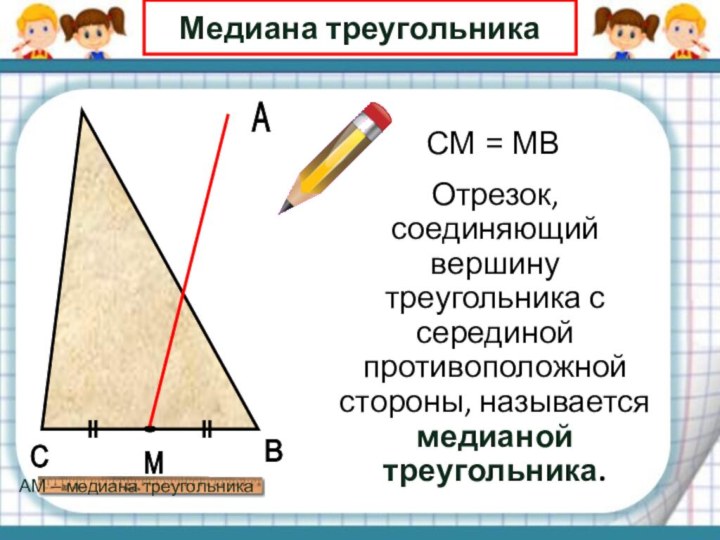
АМ – медиана треугольника

Слайд 6 В любом треугольнике медианы пересекаются в одной точке.

В любом треугольнике медианы пересекаются в одной точке. Медианы в треугольнике


Медианы в треугольнике

Слайд 7 А
В
А
Отрезок биссектрисы угла треугольника, соединяющий

А В А Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с

вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.



С

1

Биссектриса треугольника

АА1 – биссектриса треугольника



Слайд 8 В любом треугольнике биссектрисы пересекаются в одной точке.

В любом треугольнике биссектрисы пересекаются в одной точке. Биссектрисы в треугольнике.


Биссектрисы в треугольнике
.

Слайд 9 А
В
Н
Перпендикуляр, проведенный из вершины треугольника

А В Н Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей


к прямой, содержащей противоположную сторону, называется высотой
треугольника.

С
АН

– высота треугольника



Высота треугольника

Слайд 10 Высоты в треугольнике

Высоты в треугольнике

Слайд 11 Существует ли равнобедренный треугольник с углами 35º, 45º?







Существует ли равнобедренный треугольник с углами 35º, 45º?

Слайд 12 ПРАКТИЧЕСКАЯ РАБОТА
Изобразите в тетради равнобедренные треугольники

ПРАКТИЧЕСКАЯ РАБОТА Изобразите в тетради равнобедренные треугольники ( тупоугольный, остроугольный

( тупоугольный, остроугольный и прямоугольный). Выполните измерение их углов

при их основаниях и запишите результат.
Какую гипотезу можно сформулировать о величинах углов при основании равнобедренного треугольника?

Слайд 13 В равнобедренном треугольнике углы при основании равны

В равнобедренном треугольнике углы при основании равны

Слайд 14
R
T
S

Q
P
R

65˚
75˚
50˚
120˚
30˚
40˚
100˚
45˚
45˚
Найдите ошибку в решении задач

RTSQPR65˚75˚50˚120˚30˚40˚100˚45˚45˚ Найдите ошибку в решении задач

Слайд 15 Верныйрезультат

R
T
S

Q
P
R

65˚
65˚
50˚
120˚
30˚
30˚
90˚
45˚
45˚

ВерныйрезультатRTSQPR65˚65˚50˚120˚30˚30˚90˚45˚45˚

Слайд 16 Физкультминутка.
Упражнения для глаз. Нарисовать ими следующие геометрические фигуры:
правильный

Физкультминутка.Упражнения для глаз. Нарисовать ими следующие геометрические фигуры:правильный треугольник;окружность по часовой

треугольник;

окружность по часовой стрелке, а потом против;
прямоугольник;

параллелограмм;

трапецию


Слайд 17

ПРАКТИЧЕСКАЯ РАБОТА Возьмите треугольник из цветной бумаги.

ПРАКТИЧЕСКАЯ РАБОТА

Возьмите треугольник из цветной бумаги.
Методом сложения

поделите угол А пополам.
Обозначьте получившуюся на стороне ВС точку буквой Д.
Выполните измерения
Что вы заметили? Что вас удивило?
Поделитесь своим результатом с соседом по парте.
Сформулируйте выводы вместе.

Слайд 18
ТЕОРЕМА :

Биссектриса равнобедренного треугольника является

ТЕОРЕМА : Биссектриса равнобедренного треугольника является одновременно его медианой и высотой

одновременно его медианой и высотой



Слайд 19

Слайд 20 А
В
С
К
∆ АВС –равнобедренный,
АС – основание,
ВК – биссектриса.
АС

АВСК∆ АВС –равнобедренный,АС – основание, ВК – биссектриса.АС = 10 смНайти

= 10 см
Найти АК.
D
А
С
В
DA – медиана равнобедренного
∆ ВDС,

проведенная к основанию СВ.
Найдите углы ∆ АDС ,
если

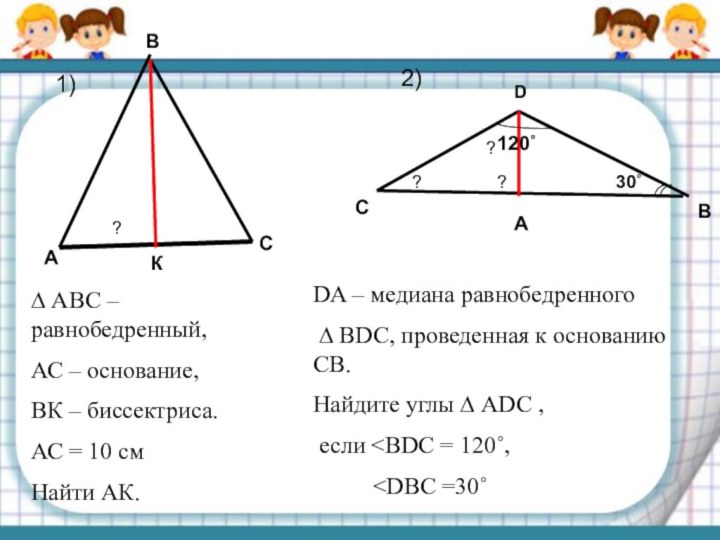
30˚

120˚




?

?

?


?

2)

1)

Слайд 21 Задача № 3

АВ=АС, АD ┴ ВС

Задача № 3АВ=АС, АD ┴ ВС < ВАD=20º, ВD=2 смНайти DС и

ВАD=20º, ВD=2 см

Найти DС и

Слайд 22 Задача № 4

АВ=АС,

Задача № 4АВ=АС,

ВD=5 см

Найти

Слайд 23 Домашнее

Домашнее заданиеГлава 3, п.2(теоремы 3,4). № 133,

задание
Глава 3, п.2(теоремы 3,4). № 133, 135;
Творческое задание: Проверить

обладают ли биссектрисы, медианы и высоты, проведенные к боковым сторонам равнобедренного треугольника открытыми свойствами.

Спасибо за урок

Спасибо за урок

  • Имя файла: prezentatsiya-k-uroku-svoystva-ravnobedrennogo-treugolnika.pptx
  • Количество просмотров: 165
  • Количество скачиваний: 0
- Предыдущая Вред и польза сотового телефона
Следующая - Презентация по истории 17 века (7 класс)

Похожие презентации

Квадрат и прямоугольник Квадрат и прямоугольник 173
Треугольник и его элементы Треугольник и его элементы 184
Правильные многогранники (11 класс) Правильные многогранники (11 класс) 150
Презентация по математике на тему Задачи ЕГЭ Презентация по математике на тему Задачи ЕГЭ 143
Урок геометрии в 8а классе Урок геометрии в 8а классе 140
Призма. Прямая и наклонная Призма. Прямая и наклонная 159
Аксиома параллельных прямых Аксиома параллельных прямых 190
Квадратное уравнение Квадратное уравнение 166
Задачи по геометрии Многогранники 9 кл Задачи по геометрии Многогранники 9 кл 160
Нахождение расстояния между точкой и прямой Нахождение расстояния между точкой и прямой 124
Презентация по геометрии Свойства прямоугольного треугольника. Презентация по геометрии Свойства прямоугольного треугольника. 143
Объём пирамиды Объём пирамиды 171
Теорема синусов Теорема синусов 162
Элементы пирамиды Элементы пирамиды 170
Задачи на разрезание (занятие 3) Задачи на разрезание (занятие 3) 198
Урок геометрии по теме теорема Пифагора Урок геометрии по теме теорема Пифагора 133
Правильные выпуклые многогранники Правильные выпуклые многогранники 169
фпвп фпвп 198
Презентация по геометрии для 8 класса по теме Свойства четырёхугольников Презентация по геометрии для 8 класса по теме Свойства четырёхугольников 68
Объём шара Объём шара 186
Касательная и окружности 8 класс Касательная и окружности 8 класс 208
Объем прямой призмы Объем прямой призмы 148
Свойства равнобедренного Свойства равнобедренного 149
Презентация Отношение площадей подобных треугольников Презентация Отношение площадей подобных треугольников 178
Подобные треугольники Подобные треугольники 137
Презентация к уроку по геометрии 2 и 3 признаки подобия треугольнов Презентация к уроку по геометрии 2 и 3 признаки подобия треугольнов 175
Презентация по геометрии на тему Симметрия Виды симметрии Презентация по геометрии на тему Симметрия Виды симметрии 146
Построение сечений тетраэдра Построение сечений тетраэдра 162
Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника 151
Многоугольники Многоугольники 152