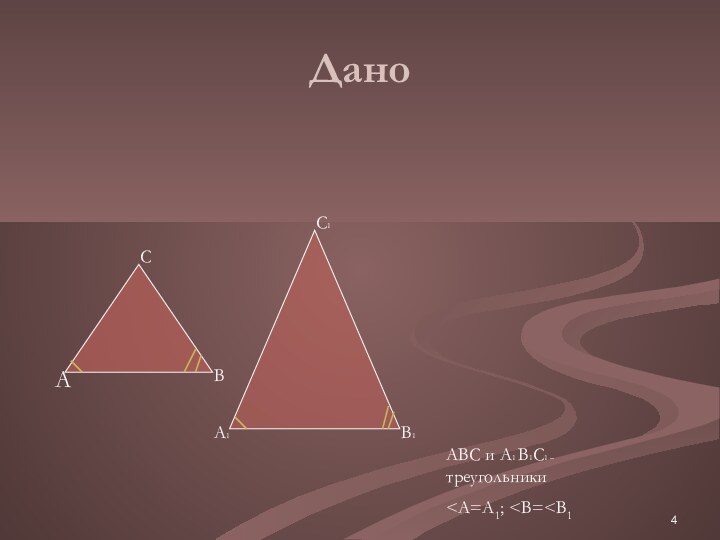
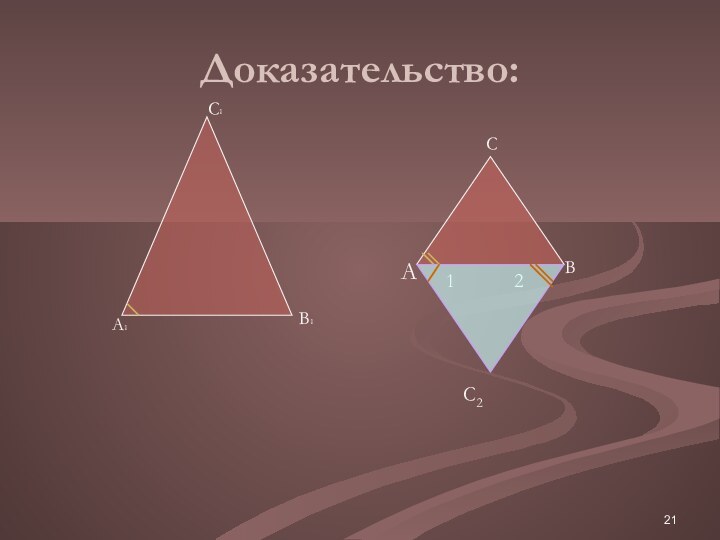
углы соответственно равны и стороны одного треугольника пропорциональны сходственным
сторонам другого.B
C
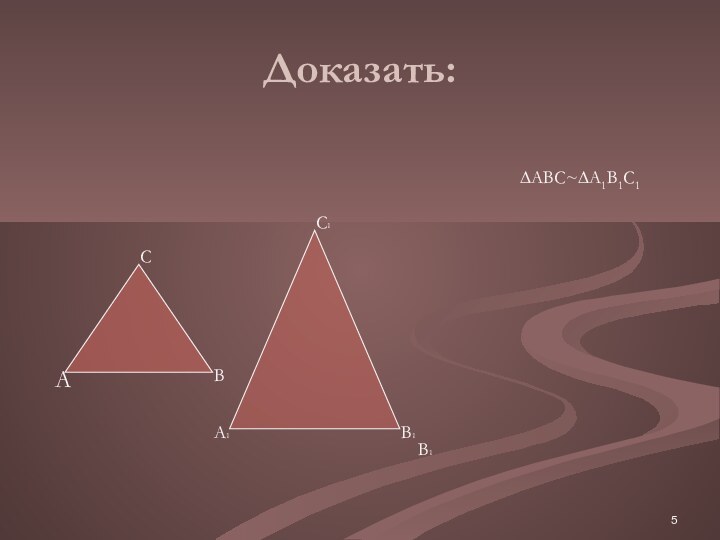
∆ABC~∆A1B1C1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















B
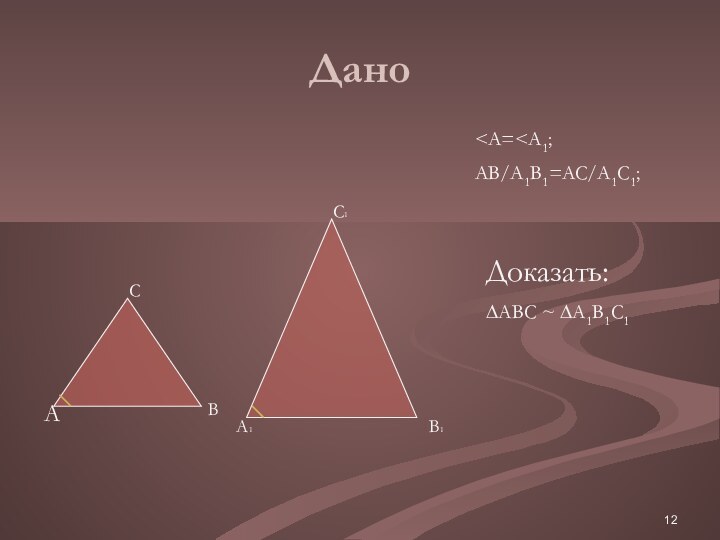
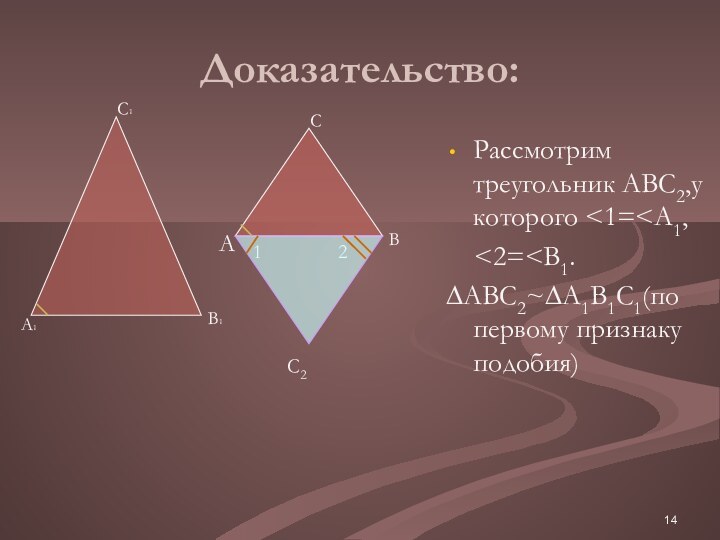
C
∆ABC~∆A1B1C1