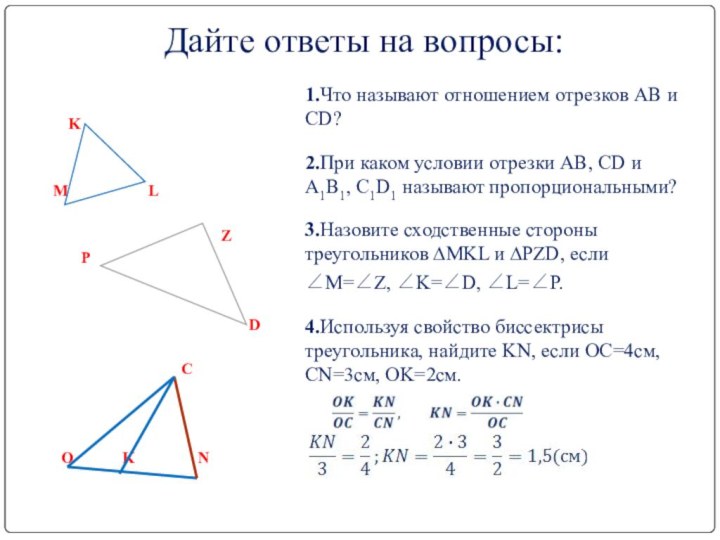
и CD?
2.При каком условии отрезки AB, CD и A1B1,
C1D1 называют пропорциональными?3.Назовите сходственные стороны треугольников ∆MKL и ∆PZD, если
∠M=∠Z, ∠K=∠D, ∠L=∠P.
4.Используя свойство биссектрисы треугольника, найдите KN, если OC=4см, CN=3см, OK=2см.
K
M L
Z
P
D
C
O K N