- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрические преобразования и паркеты
Содержание
- 2. «Математика владеет не только истиной, но и
- 4. Геометрические паркеты Паркет (или мозаика) - бесконечное
- 5. Паркеты из одинаковых правильных многоугольников. Можно
- 6. Паркеты из разных правильных многоугольников.Существуют следующие способы
- 7. Некоторые варианты паркета показаны на следующих иллюстрациях:
- 8. Паркеты из неправильных многоугольников. Легко покрыть плоскость
- 9. Можно составить паркет из копий произвольного треугольника:
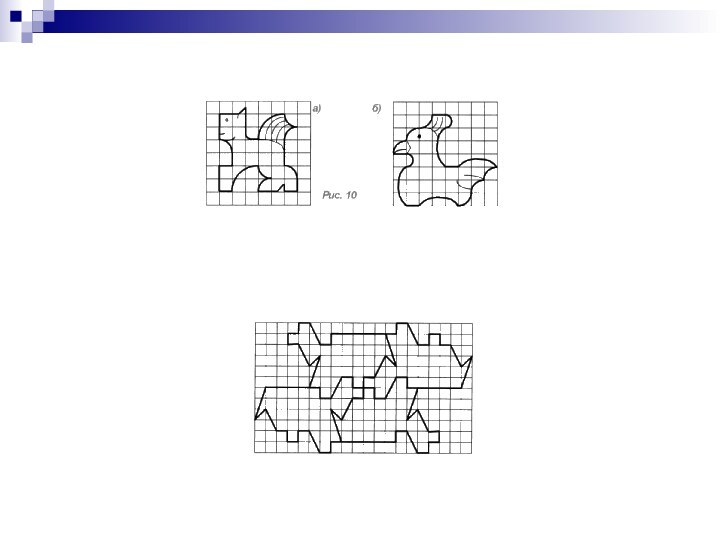
- 10. Паркеты из невыпуклых семиугольников
- 11. Паркеты из произвольных фигур. Некоторые определения паркета
- 12. Паркеты, полученные заменой отрезков "квадратной" сетки некоторыми кривыми или ломаными.
- 13. Паркеты, полученные в результате объединения элементов квадратной сетки
- 14. Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников
- 15. Разбиения сетки из греческих крестов
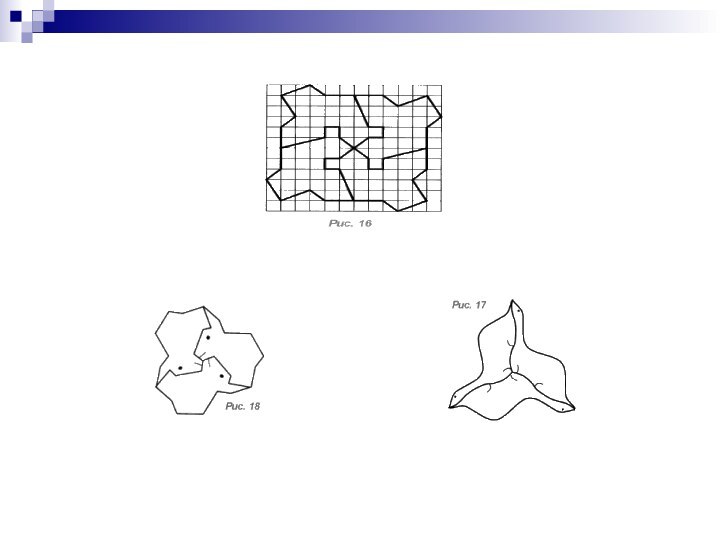
- 16. Паркеты, полученные с помощью параллельного переноса
- 17. Паркеты Мориса Эшера
- 18. Плитки Пенроуза .
- 19. Практическая часть.Простейшим видом паркета является такой, в
- 22. Каждой из фигурок заполните плоскость, получив паркет.
- 23. Сравните фигурки. Скопируйте их на кальку и заполните плоскость, получив паркет.
- 25. Скачать презентацию
- 26. Похожие презентации
«Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».