Слайд 2
Геометрия
Планиметрия
Стереометрия
stereos
телесный, твердый, объемный, пространственный
Слайд 3
это подраздел геометрии, изучающий свойства фигур в пространстве
Стереометрия
Слайд 4
Пространство - это множество, элементами которого являются точки
и в котором выполняется система аксиом стереометрии, описывающая свойства
точек, прямых и плоскостей
stereos
Слайд 5
Для изучения стереометрии
Надо научиться делать чертежи и уметь
читать их.
Правильный чертеж поможет понять, представить и проиллюстрировать содержание
задачи.
Ключ к изучению стереометрии - пространственное воображение в сочетании с логикой мышления.
Слайд 6
Стереометрия
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка
а
Прямая
Плоскость
Слайд 7
Слово «стереометрия» происходит от греческих слов «стереос» объемный,
пространственный, «метрео» – мерить.
Основные фигуры: точка, прямая, плоскость.
Слайд 8
A, B, C, …
a, b, c, …
или
AВ, BС,
CD, …
Слайд 9
Для обозначения точек как и в планиметрии используют
прописные латинские буквы:
Прямую обозначают одной строчной латинской буквой и
двумя прописными латинскими буквами:
Слайд 10
Плоскость в стереометрии обозначают греческими буквами, например:
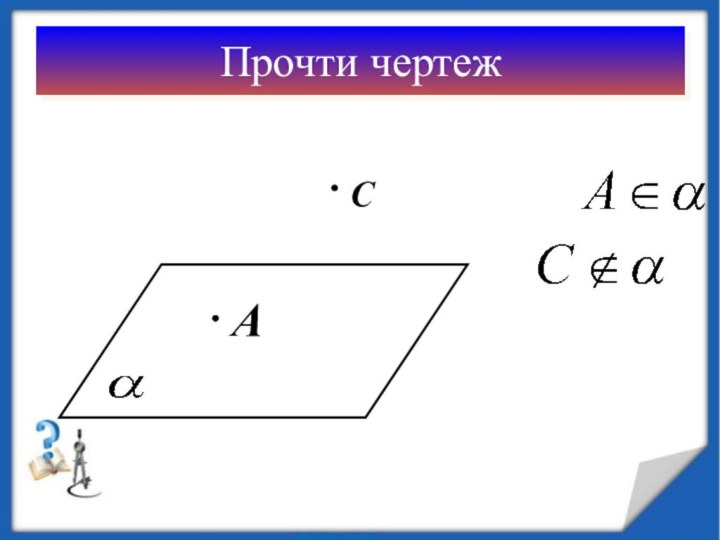
А
на рисунках чаще всего плоскость изображают в виде параллелограмма.
Но следует понимать и представлять себе данную геометрическую фигуру как неограниченную во все стороны.
Слайд 11
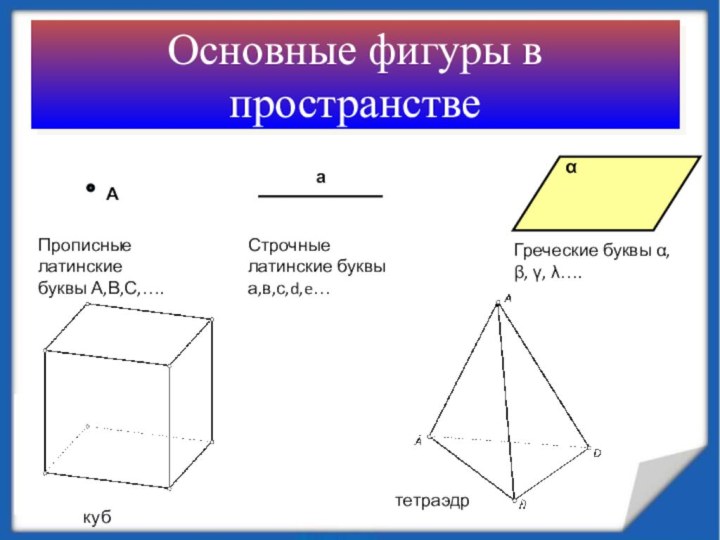
А
а
α
Прописные латинские буквы А,В,С,….
Строчные латинские буквы а,в,с,d,e…
Греческие буквы
α, β, γ, λ….
куб
тетраэдр
Основные фигуры в пространстве
Слайд 12
Наряду с основными фигурами мы будем рассматривать геометрические
тела и их поверхности. Такие, как: куб, параллелепипед, призма,
пирамида.
А также тела вращения: шар, сфера, цилиндр, конус.
Слайд 13
Обозначение точки: А; В; С; М …
Обозначение прямой:
а; b,с h или АВ, ВС…
Плоскости - это фигуры,
на которых выполняется планиметрия и для которых верны аксиомы стереометрии.
Обозначения плоскостей:
Основные понятия стереометрии
A , KC , С
b
Слайд 17
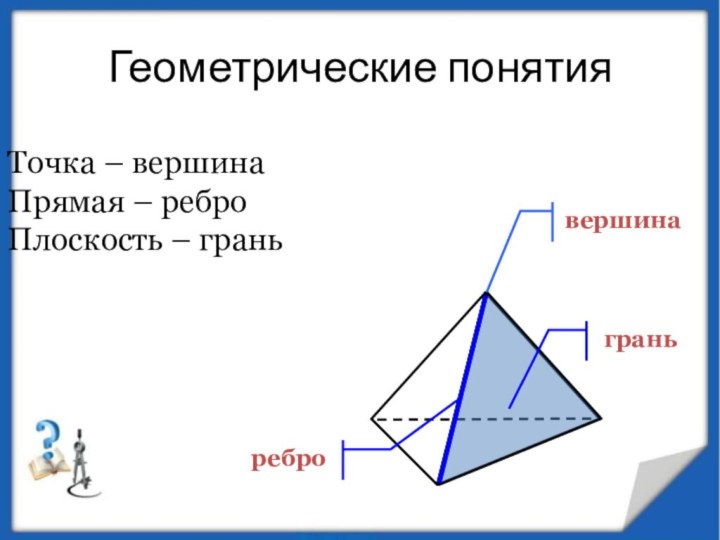
Геометрические понятия
Точка – вершина Прямая – ребро Плоскость
– грань
вершина
грань
ребро
Слайд 18
При изучении в курсе стереометрии геометрических тел пользуются
их плоскими изображениями на чертеже.
Изображением пространственной фигуры служит
ее проекция на плоскость.
Изображения конуса
Слайд 19
Изучая свойства геометрических фигур – воображаемых объектов, мы
получаем представление о геометрических свойствах реальных предметов (их форме,
взаимном расположении и т. д.) и можем использовать эти свойства в практической деятельности. В этом состоит прикладное значение геометрии.
Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих
других областях науки и техники.
Слайд 20
Основные свойства точек, прямых и плоскостей выражены в
аксиомах. Существует множество аксиом стереометрии, в учебнике вам представлены
три:
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
A
B
C
Слайд 21
Древнее представление о земле - пример к аксиоме
Слайд 22
Древнее представление о земле - пример к аксиоме
Слайд 23
Самый простой пример к аксиоме А1 из повседневной
жизни:
Табурет с тремя ножками всегда идеально встанет на пол
и не будет качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине.
Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости
пола, а висит в воздухе.
Слайд 24
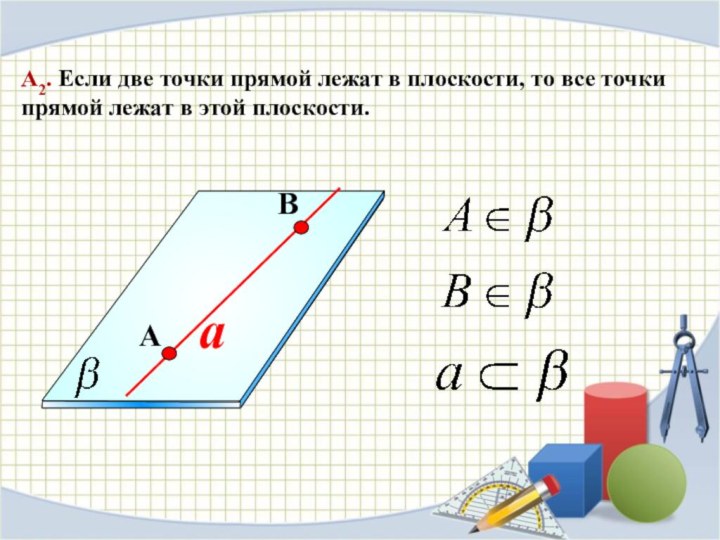
a
А2. Если две точки прямой лежат в плоскости,
то все точки прямой лежат в этой плоскости.
A
B
Слайд 25
Свойство, выраженное в аксиоме А2, используется для проверки
«ровности» чертежной линейки.
Линейку прикладывают краем к плоской поверхности
стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола.
Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.
Слайд 26
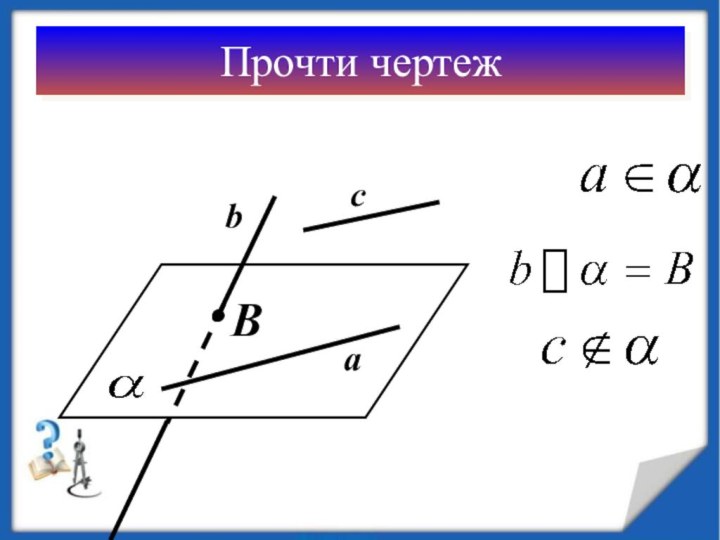
Следствия из аксиомы А2:
Если прямая не лежит
в данной плоскости, то она имеет с ней не
более одной общей точки.
Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
Слайд 27
a
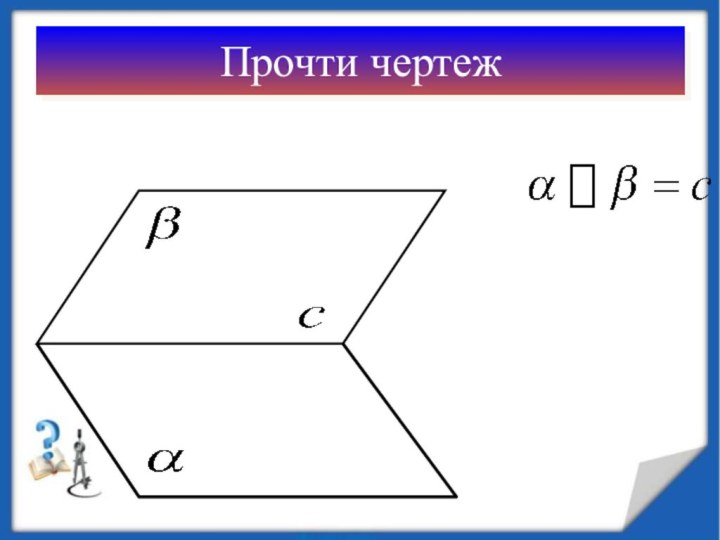
А3. Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
Самый простой пример к аксиоме А3 из повседневной жизни является пересечение двух смежных стен комнаты.
Слайд 28
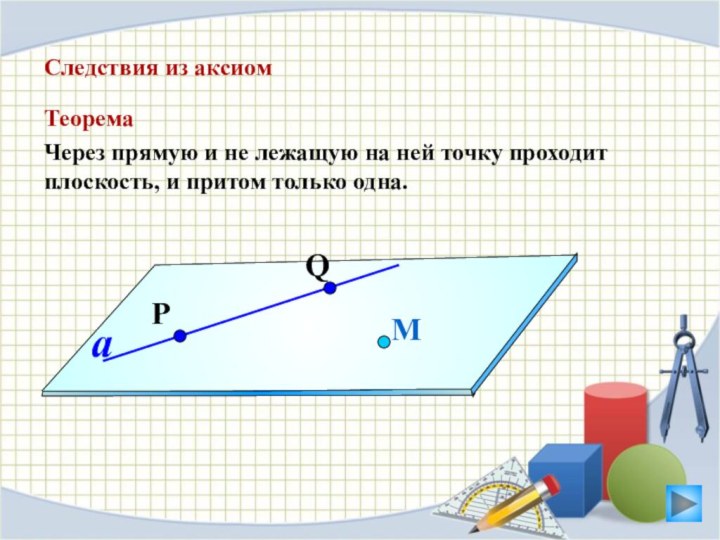
Следствия из аксиом
Теорема
Через прямую
и не лежащую на ней точку проходит плоскость, и
притом только одна.
М
a
Слайд 29
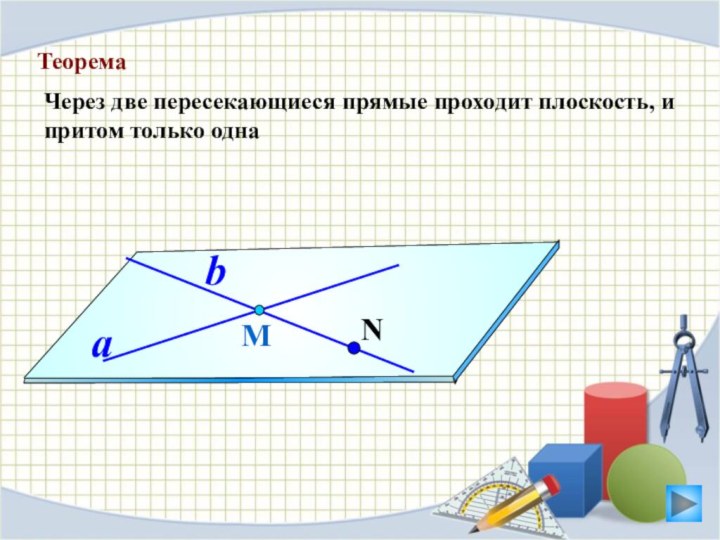
Теорема
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
М
a
b
N
Слайд 30
Устная работа.
Д
Дано: куб АВСДА1В1С1Д1
Найдите:
Несколько точек, которые лежат в
плоскости α;
Несколько точек, которые не лежат в плоскости α;
Несколько
прямых, которые лежат в плоскости α;
Несколько прямых, которые не лежат в плоскости α;
Несколько прямых которые пересекают прямую ВС;
Несколько прямых, которые не пересекают прямую ВС.
Задача 1.
Слайд 31
Устная работа.
Задача 2.
α
А
М
В
а
b
c
Заполните пропуски, чтобы получилось верное утверждение:
Слайд 32
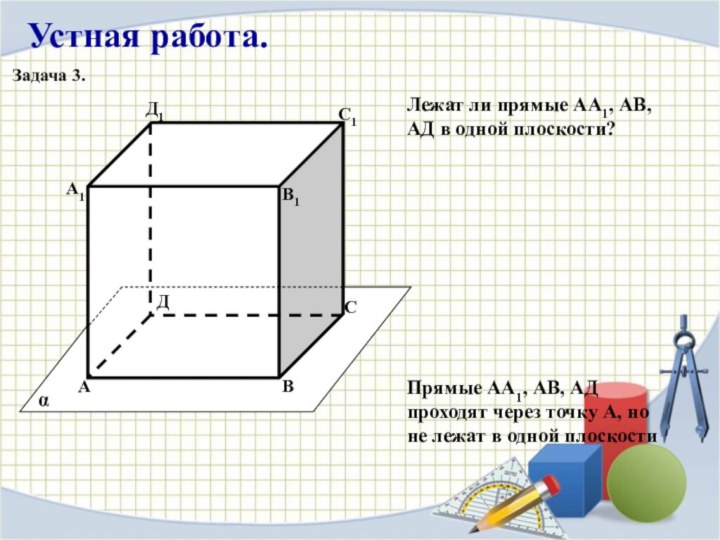
Устная работа.
А
В
С
Д
А1
В1
С1
Д1
α
Прямые АА1, АВ, АД проходят через точку
А, но не лежат в одной плоскости
Лежат ли прямые
АА1, АВ, АД в одной плоскости?
Задача 3.
Слайд 34
Задача 1
Назовите плоскости, в которых лежат
прямые
РЕ, МК, DB, AB, EC
Назовите точки пересечения прямой DK
с плоскостью АВС
Назовите точки, лежащие в плоскостях АDB и DBC
P
E
A
B
C
D
M
K
Слайд 35
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
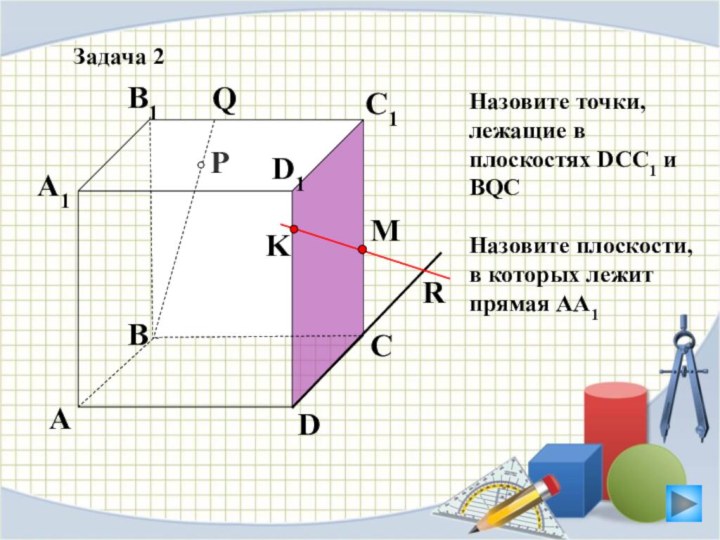
Задача 2
Назовите точки, лежащие в плоскостях
DCC1 и BQC
Назовите плоскости, в которых лежит прямая АА1
Слайд 36
Задача 4
Дано: куб АВСДА1В1С1Д1
Точка М лежит на
ребре ВВ1, т.N лежит на ребре СС1 и точка
К лежит на ребре ДД1
а) назовите плоскости, в которых лежат точки М; N.
б) найдите т.F-точку пересечения прямых МN и ВС. Каким свойством обладает точка F?
в) найдите точку пересечения прямой КN и плоскости АВС
г) найдите линию пересечения плоскостей МNК и АВС
Слайд 37
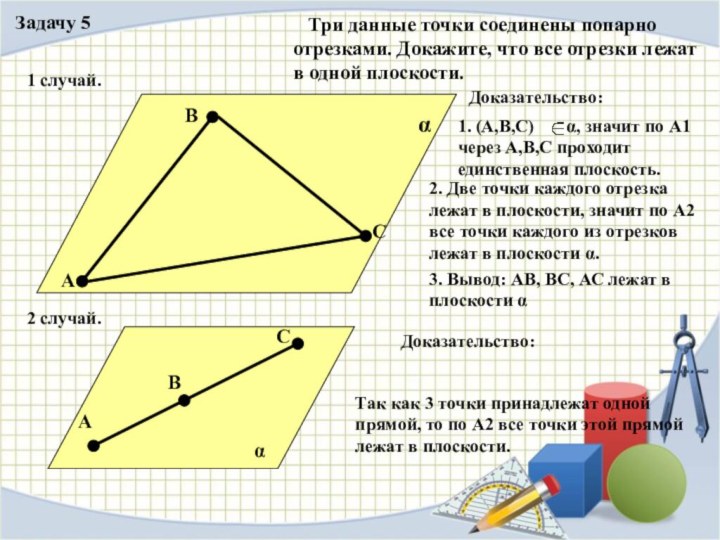
Задачу 5
А
В
С
α
Три данные точки соединены попарно
отрезками. Докажите, что все отрезки лежат в одной плоскости.
Доказательство:
1.
(А,В,С) α, значит по А1 через А,В,С проходит единственная плоскость.
2. Две точки каждого отрезка лежат в плоскости, значит по А2 все точки каждого из отрезков лежат в плоскости α.
3. Вывод: АВ, ВС, АС лежат в плоскости α
1 случай.
А
В
С
α
2 случай.
Доказательство:
Так как 3 точки принадлежат одной прямой, то по А2 все точки этой прямой лежат в плоскости.
Слайд 38
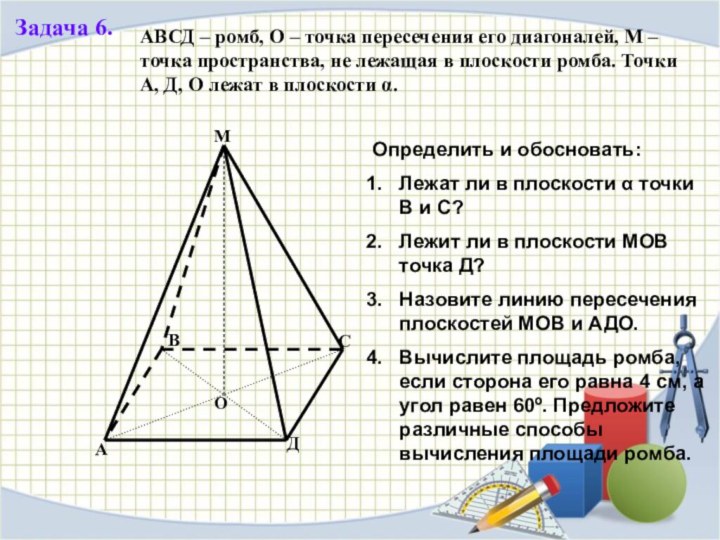
Задача 6.
А
В
С
Д
М
О
АВСД – ромб, О – точка пересечения
его диагоналей, М – точка пространства, не лежащая в
плоскости ромба. Точки А, Д, О лежат в плоскости α.
Определить и обосновать:
Лежат ли в плоскости α точки В и С?
Лежит ли в плоскости МОВ точка Д?
Назовите линию пересечения плоскостей МОВ и АДО.
Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60º. Предложите различные способы вычисления площади ромба.
Слайд 39
А
В
С
Д
60º
4
4
4
4
SАВСД = АВ · АД · sinA
SАВСД
= (ВД · АС):2
Формулы для вычисления площади ромба:
∆АВД
= ∆ВСД (по трем сторонам), значит SАВД = SВСД.
Слайд 40
Задача №1
А
В
С
М
Р
Е
Д
F
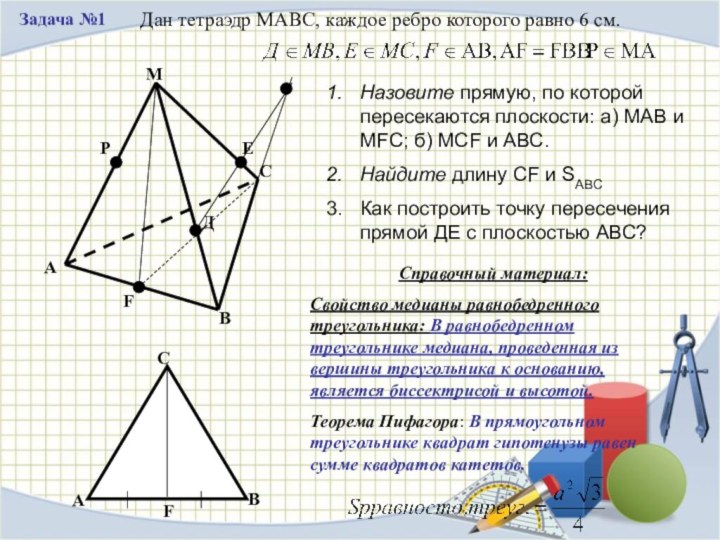
Дан тетраэдр МАВС, каждое ребро которого равно
6 см.
Назовите прямую, по которой пересекаются плоскости: а)
МАВ и МFС; б) МСF и АВС.
Найдите длину СF и SАВС
Как построить точку пересечения прямой ДЕ с плоскостью АВС?
А
В
С
F
Справочный материал:
Свойство медианы равнобедренного треугольника: В равнобедренном треугольнике медиана, проведенная из вершины треугольника к основанию, является биссектрисой и высотой.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 41
А
В
С
Д
А1
В1
С1
Д1
Задача №2
Как построить точку пересечения плоскости АВС с
прямой Д1Р?
Как построить линию пересечения плоскости АД1Р и АВВ1?
Вычислите
длину отрезков АР и АД1, если АВ = а
Р
К
Слайд 42
Задача №3
А
В
М
Р
С
К
Дано: Точки А, В, С не лежат
на одной прямой.
Докажите, что точка Р лежит в плоскости
АВС.
α
Слайд 43
с
а
В
Задача 7
Плоскости и
пересекаются по прямой с. Прямая а
лежит в плоскости и пересекает плоскость . Пересекаются ли прямые а и с? Почему?
Слайд 44
Задача 8
А
В
С
Д
О
60º
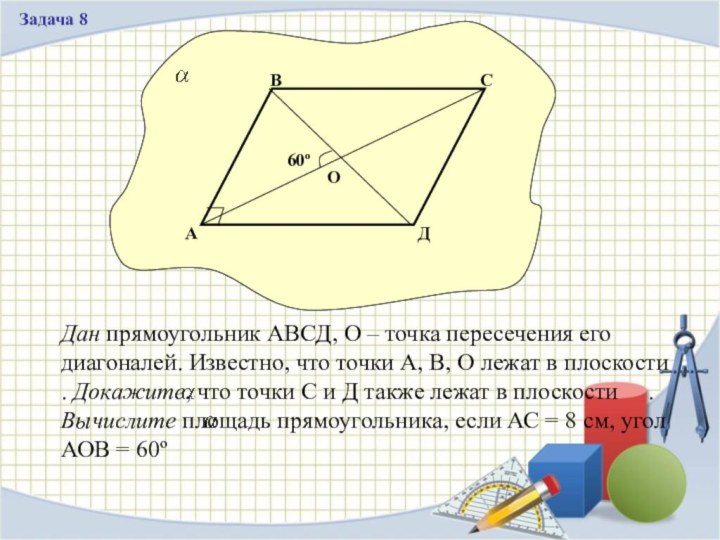
Дан прямоугольник АВСД, О – точка пересечения
его диагоналей. Известно, что точки А, В, О лежат
в плоскости . Докажите, что точки С и Д также лежат в плоскости . Вычислите площадь прямоугольника, если АС = 8 см, угол АОВ = 60º
Слайд 45
Домашнее задание:
1. Прочитать пункты 1; 2; 3
на стр. 3 – 7
2. Выучить теоремы 1, 2
( с доказательством); повторить аксиомы А1 – А3
3. Решить задачи №8, 9, 11, 13 ( с объяснением ответов)
Слайд 46
Интернет-ресурсы
http://gym1.ucoz.ru/load/1-1-0-145. Источник шаблона: Ранько Елена Алексеевна учитель начальных
классов МАОУ лицей №21 г. Иваново
2. Циркуль: http://www.daviddarling.info/images/compasses.jpg
3. Карандаш: http://www.proshkolu.ru/content/media/pic/std/3000000/2240000/2239093-7acd9447b354cc7e.gif
4. Угольник-транспортир: http://p.alejka.pl/i2/p_new/25/38/duza-ekierka-geometryczna-z-uchwytem-rotring-14-cm_0_b.jpg
5. Фон «тетрадная клетка»: http://radikal.ua/data/upload/49112/4efc3/3bd0a3d6bb.jpg
6. http://nsportal.ru/ap/ap/drugoe/2012/04/20/prezentatsiya-po-teme-stereometriya