точек плоскости,
расположенных на заданном расстоянии от
данной точки.
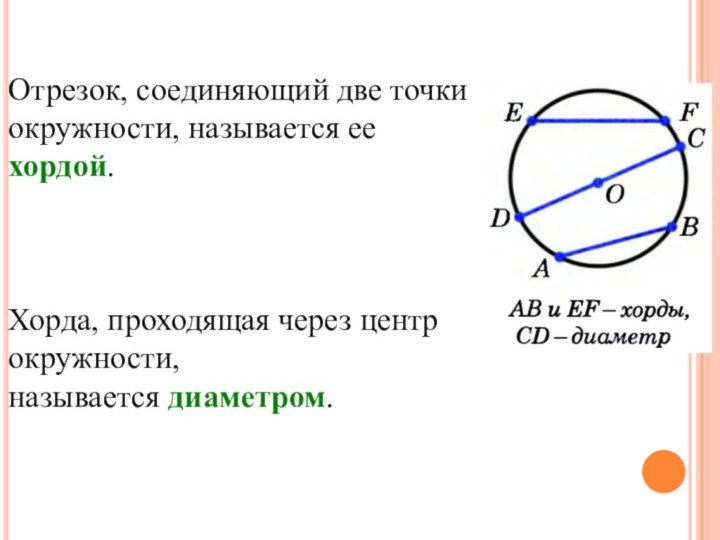
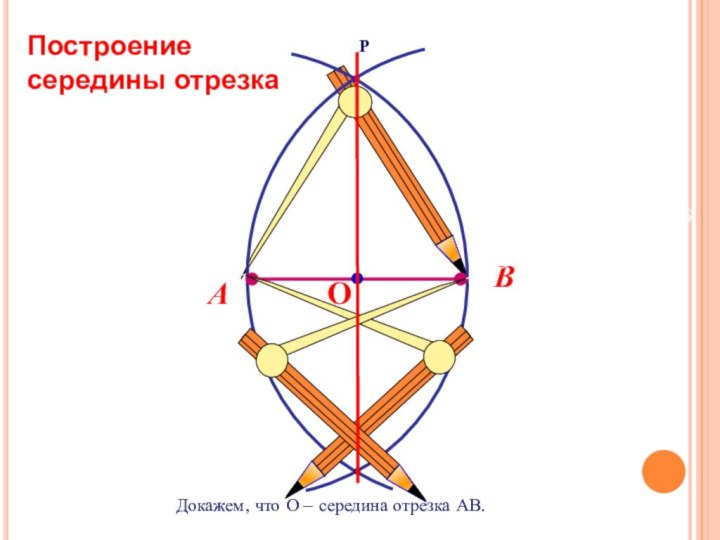
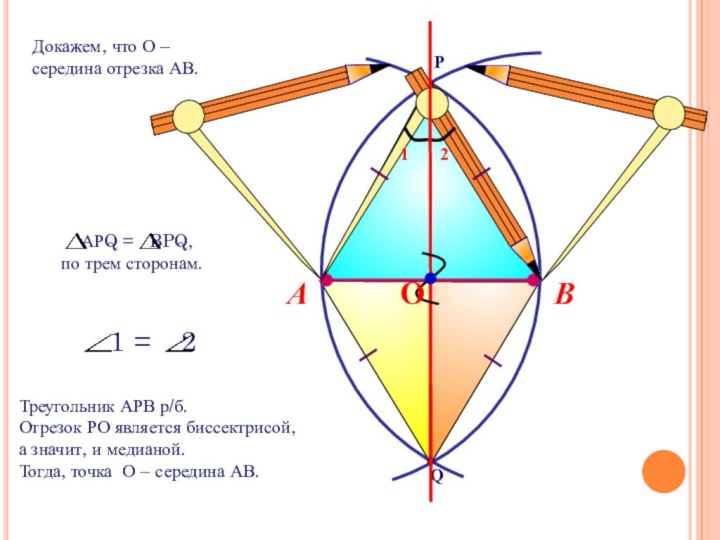
Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.