- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Ломаная
Содержание
- 2. Простая ломанаяЛоманая с самопересечениемАВСDАВСDEEAB+BC+CD+DE – длина ломаной
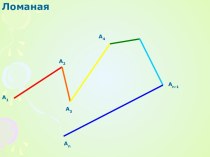
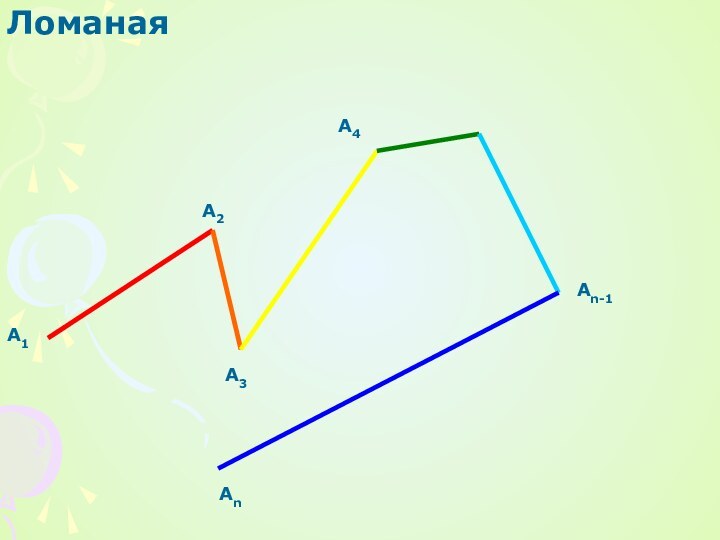
- 3. А1А2А3А4Аn-1АnТЕОРЕМА 13.1Длина ломаной не меньше длины отрезка, соединяющего ее концы
- 4. ЛоманаяА1А3А4Аn-1АnА2По неравенству треугольникаA1A3
- 5. ЛоманаяА1А3А4Аn-1АnА2По неравенству треугольникаA1A4
- 6. А1А3А4Аn-1АnА2Соединяя концы ломанойПридем к отрезкуА1АnДлина данной ломанойНе меньше длины А1АnТеорема доказана
- 7. Вопросы1. Какая фигура называется ломаной?2. Что называют
- 8. Решение задач№6 – устно2. Найдите длину ломаной
- 9. Скачать презентацию
- 10. Похожие презентации
Простая ломанаяЛоманая с самопересечениемАВСDАВСDEEAB+BC+CD+DE – длина ломаной








Слайд 6
А1
А3
А4
Аn-1
Аn
А2
Соединяя концы ломаной
Придем к отрезкуА1Аn
Длина данной ломаной
Не меньше
длины А1Аn
Теорема доказана
Слайд 7
Вопросы
1. Какая фигура называется ломаной?
2. Что называют вершиной
ломаной?
3. Что называют звеном ломаной
4. Когда ломаная будет прямой?
5.
Когда ломаная будет с самопересечением?6. Сформулируйте теорему 13.1.
Слайд 8
Решение задач
№6 – устно
2. Найдите длину ломаной А1А2А3А4А5А6,
если А1, А2, А3, А4 – вершины квадрата со
стороной 2см, А5 – точка пересечения диагоналей, А6 – середина А1А43. Докажите, что длина ломаной А1А2А3А4 больше длины ломаной А1А3А4