Презентация на тему Геометрические задачи С2

Без сильного желания решить трудную задачу невозможно, но при

точку, есть длина перпендикуляра, проведенного из этой точки на

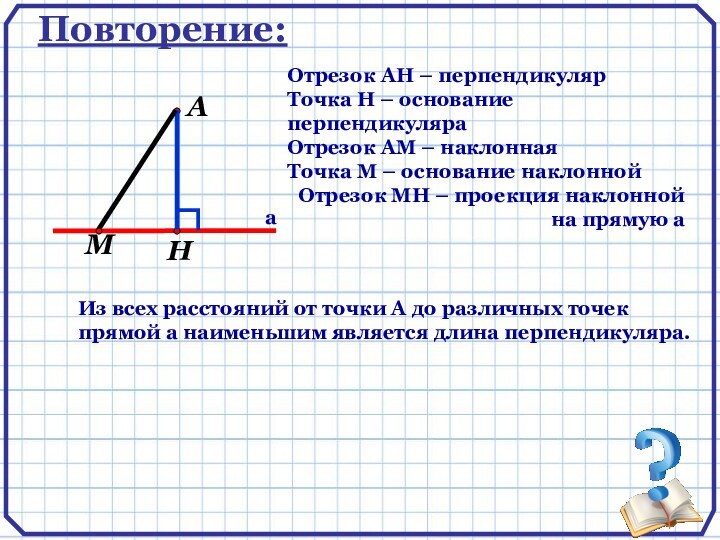
1) Как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;

Расстояние от точки до прямой можно вычислить:

2) Используя координатно – векторный метод;

АМ – наклонная
Точка М – основание наклонной
Отрезок МН

Из всех расстояний от точки А до различных точек прямой а наименьшим является длина перпендикуляра.

А до прямой ВД1.
№ 1


1
1
1
1


М
1) Построим плоскость AD1В, проведем

2) Найдем искомое расстояние через вычисление площади треугольника AD1В.

В до прямой ДА1.
№ 2

Данный чертеж не является наглядным

Попробуем развернуть куб …

В до прямой ДА1.
№ 2
1) Построим плоскость DВA1, проведем

М

Решить самостоятельно …..

1

1

1

1

1

которой равны 1,
найдите расстояние от точки В до прямой

№ 3

1

1

1

1

1

1) Построим плоскость АВС1, проведем из точки В перпендикуляр. ВМ – искомое расстояние.

М

Решить самостоятельно …..

равны 1, а боковые ребра равны 2,
найдите расстояние от

№ 4

1

1

1

2

2

М

1) Построим плоскость FSВ, проведем из точки S перпендикуляр. SМ – искомое расстояние.

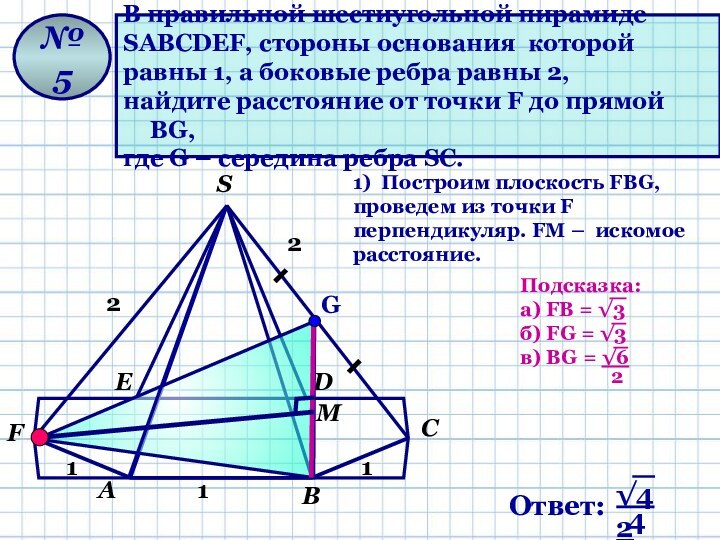
Подсказка:
а) ∠FАВ = 1200
б) Рассмотреть прямоугольный ∆АВМ

равны 1, а боковые ребра равны 2,
найдите расстояние от

№ 5

1

1

1

2

2

М

1) Построим плоскость FВG, проведем из точки F перпендикуляр. FМ – искомое расстояние.

G

равны 1, найдите
расстояние от точки В до прямой

№ 6

1

1

1

1

М

1) Построим плоскость ВА1D1, проведем из точки В перпендикуляр. ВМ – искомое расстояние.

Решить самостоятельно …..

равны 1, найдите
расстояние от точки А до прямой

№ 7

1

1

1

1

1) Построим плоскость АF1D1, так как прямая F1D1 перпендикулярна плоскости АFF1, то отрезок АF1 будет искомым перпендикуляром.

Решить самостоятельно …..

равны 1, найдите
расстояние от точки В до прямой

№ 8

1

1

1

1

М

1) Построим плоскость ВА1F1, проведем из точки В перпендикуляр. ВМ – искомое расстояние.

А

Решить самостоятельно …

Н

А до прямой:
а) В1Д1; б) А1С
Домашнее задание
В правильной