- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площадь поверхности конуса
Содержание
- 2. УРОК ГЕОМЕТРИИ В 11 КЛАССЕТема: КОНУС. ПЛОЩАДЬ ПОВЕРХНОСТИ КОНУСА.
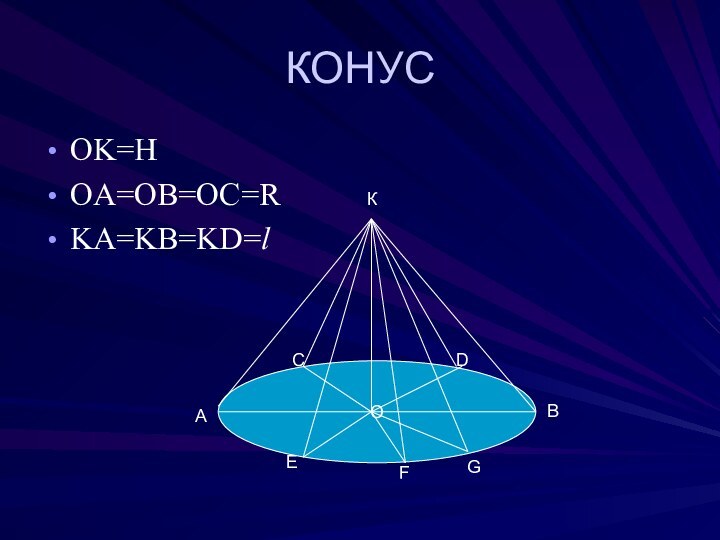
- 3. КОНУСOK=HOA=OB=OC=RKA=KB=KD=lОАВКСDEFG
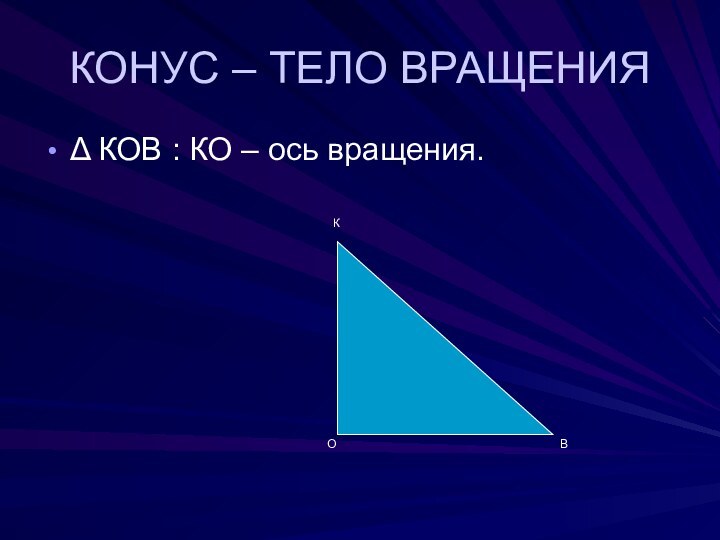
- 4. КОНУС – ТЕЛО ВРАЩЕНИЯΔ КОВ : КО – ось вращения.КОВ
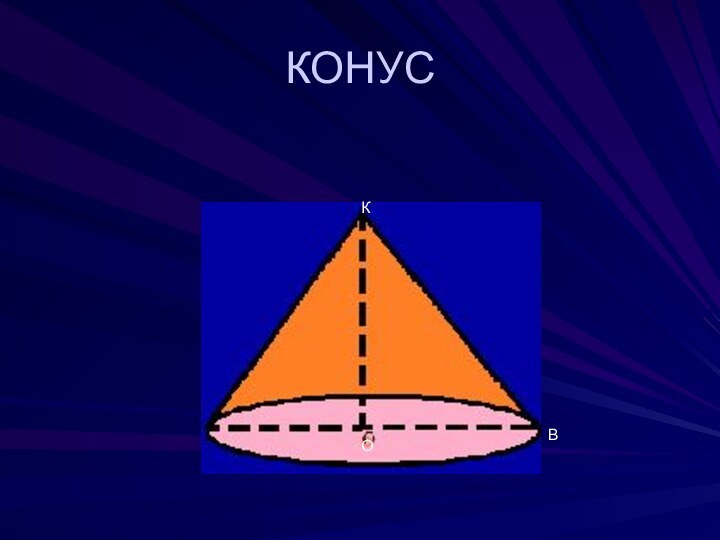
- 5. КОНУСКВО
- 6. РАЗВЁРТКА БОКОВОЙ ПОВЕРХНОСТИ КОНУСА – круговой секторAK=lПЛОЩАДЬ КРУГА:
- 7. РАЗВЁРТКА БОКОВОЙ ПОВЕРХНОСТИ КОНУСА – круговой сектор.AK=lПЛОЩАДЬ КРУГА: S=πl2α
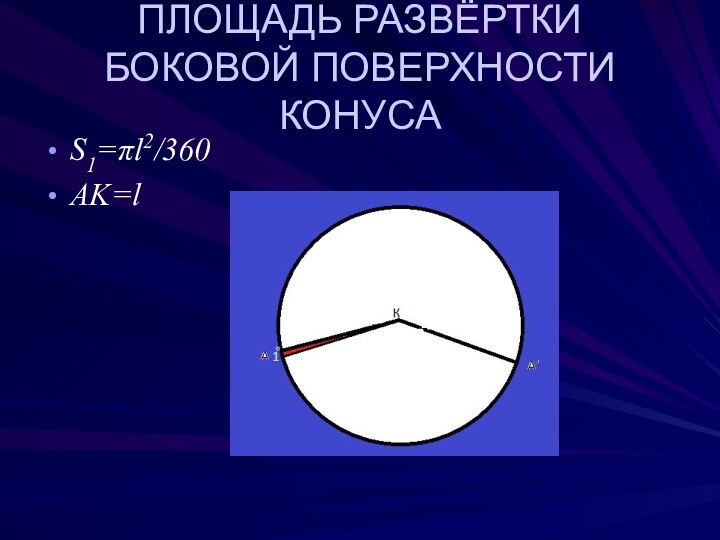
- 8. ПЛОЩАДЬ РАЗВЁРТКИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСАS1=πl2/360AK=l
- 9. ПЛОЩАДЬ РАЗВЁРТКИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСАAK = l ,< AKA’ = φφ
- 10. ПЛОЩАДЬ РАЗВЁРТКИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСАAK=l∟AKA’=φφφ
- 11. ПРАКТИЧЕСКАЯ РАБОТА1. ИЗГОТОВЬТЕ РАЗВЁРТКУ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА.
- 12. ПРАКТИЧЕСКАЯ РАБОТА2. ИЗМЕРЬТЕ ДЛИНУ ОБРАЗУЮЩЕЙ (РАДИУС КРУГОВОГО СЕКТОРА)l=16.2 см.
- 13. ПРАКТИЧЕСКАЯ РАБОТА3. Измерьте центральный угол развёртки боковой поверхности конуса:α=122о
- 14. ПРАКТИЧЕСКАЯ РАБОТА4. Выполните вычисления по формуле:Sc= πl2 φ /360Пример:Sc= π*16,22 *122 /360≈88,94 π ≈279,4 см2 .
- 15. ПРАКТИЧЕСКАЯ РАБОТА5. Склейте из заготовки развёртки боковой поверхности модель конуса:
- 16. ПРАКТИЧЕСКАЯ РАБОТА6. Измерьте радиус основания конуса:R= 5.5 см
- 17. ПРАКТИЧЕСКАЯ РАБОТАКАК ВЫРАЗИТЬ ВЕЛИЧИНУ УГЛА φ
- 18. ПРАКТИЧЕСКАЯ РАБОТАКАК ВЫЧИСЛИТЬ ДЛИНУ ОКРУЖНОСТИ?С=2π R,АК= l,С=2π l.ll
- 19. ПРАКТИЧЕСКАЯ РАБОТАКАК ВЫЧИСЛИТЬ ДЛИНУ ДУГИ ОКРУЖНОСТИ?С1= π l /180 –длина дуги величиной 1о .
- 20. ПРАКТИЧЕСКАЯ РАБОТАКАК ВЫЧИСЛИТЬ ДЛИНУ ДУГИ ОКРУЖНОСТИ?φ
- 21. ПРАКТИЧЕСКАЯ РАБОТАДЛИНА ДУГИ АА’ СЕКТОРА РАВНА ДЛИНЕ ОКРУЖНОСТИ ОСНОВАНИЯ КОНУСА:
- 22. ПРАКТИЧЕСКАЯ РАБОТАПОДСТАВЬТЕ НАЙДЕННОЕ ВЫРАЖЕНИЕ ДЛЯ
- 23. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСАПОЛУЧАЕМ:
- 24. ФОРМУЛА ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА:SБПК = π
- 25. ПРАКТИЧЕСКАЯ РАБОТА ВЫПОЛНИТЕ
- 26. ФОРМУЛА ПЛОЩАДИ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСАSппк = Sбпк
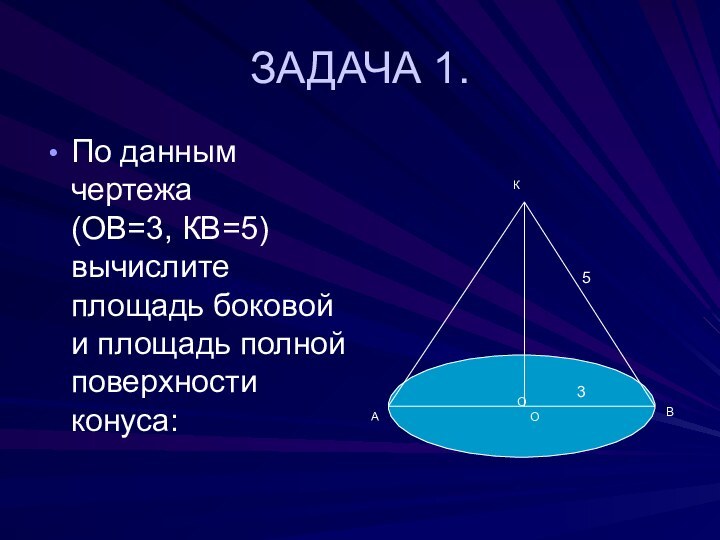
- 27. ЗАДАЧА 1.По данным чертежа
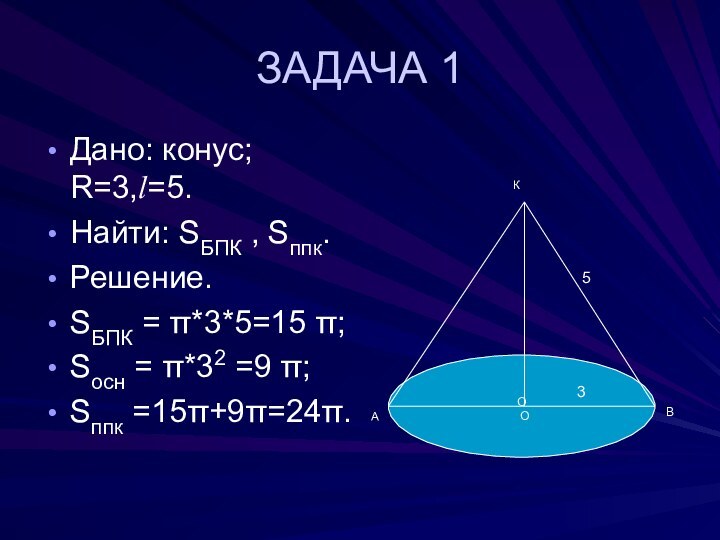
- 28. ЗАДАЧА 1Дано: конус; R=3,l=5.Найти: SБПК , Sппк.Решение.SБПК = π*3*5=15 π;Sосн = π*32 =9 π;Sппк =15π+9π=24π.ОАВК35О
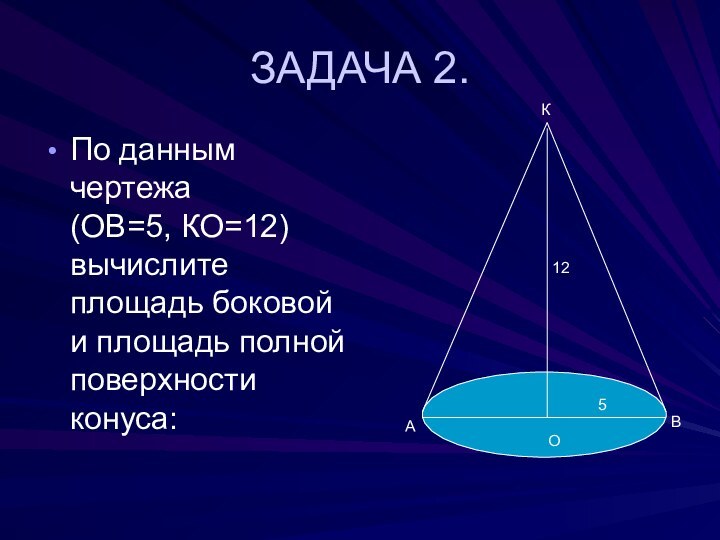
- 29. ЗАДАЧА 2.По данным чертежа
- 30. ЗАДАЧА 2.Дано: конус; R=5, h=12.Найти: SБПК ,
- 31. ЗАДАЧА 3.По данным чертежа
- 32. ЗАДАЧА 3.Дано: конус; R=6,∟АКО=30о.Найти: SБПК , Sппк.Решение.l=R/sin30о,l=6/0.5=12;SБПК=π*12*6=72π;Sосн
- 33. ЗАДАЧА 4.РАВНЫ ЛИ ПЛОЩАДИ ПОВЕРХНОСТЕЙ ДВУХ КОНУСОВ,
- 34. РЕШЕНИЕ ЗАДАЧИ 41) R=ВС= a ;
- 35. ДОМАШНЕЕ ЗАДАНИЕ: УЧЕБНИК СТЕРЕОМЕТРИИ ПОД РЕД.
- 36. Скачать презентацию
- 37. Похожие презентации
УРОК ГЕОМЕТРИИ В 11 КЛАССЕТема: КОНУС. ПЛОЩАДЬ ПОВЕРХНОСТИ КОНУСА.




























Слайд 13
ПРАКТИЧЕСКАЯ РАБОТА
3. Измерьте центральный угол развёртки боковой поверхности
конуса:
α=122о
Слайд 14
ПРАКТИЧЕСКАЯ РАБОТА
4. Выполните вычисления по формуле:
Sc= πl2 φ
/360
Пример:
Sc= π*16,22 *122 /360≈88,94 π ≈279,4 см2 .
Слайд 17
ПРАКТИЧЕСКАЯ РАБОТА
КАК ВЫРАЗИТЬ ВЕЛИЧИНУ УГЛА φ –ЦЕНТРАЛЬНОГО
УГЛА РАЗВЁРТКИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА –ЧЕРЕЗ РАДИУС ОСНОВАНИЯ
R И ДЛИНУ ОБРАЗУЮЩЕЙ l КОНУСА ?
Слайд 19
ПРАКТИЧЕСКАЯ РАБОТА
КАК ВЫЧИСЛИТЬ ДЛИНУ ДУГИ ОКРУЖНОСТИ?
С1= π l
/180 –длина дуги величиной 1о .
Слайд 22
ПРАКТИЧЕСКАЯ РАБОТА
ПОДСТАВЬТЕ НАЙДЕННОЕ ВЫРАЖЕНИЕ ДЛЯ
φ В ФОРМУЛУ
ПЛОЩАДИ РАЗВЁРТКИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА
Слайд 24
ФОРМУЛА ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА:
SБПК = π R
l
R – радиус основания,
l – длина образующей конуса.
Слайд 25
ПРАКТИЧЕСКАЯ РАБОТА
ВЫПОЛНИТЕ ВЫЧИСЛЕНИЕ
ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ МОДЕЛИ КОНУСА ПО
ФОРМУЛЕ SБПК = π R l .SБПК = π*5,5*16,2= 89,1π ≈279,9π (см2)
Слайд 26
ФОРМУЛА ПЛОЩАДИ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСА
Sппк = Sбпк +
Sосн
Sппк = πRl + π R2
Sппк = π R(R+l)
О
К
А
В
Слайд 27
ЗАДАЧА 1.
По данным чертежа
(ОВ=3, КВ=5) вычислите площадь боковой и площадь полной поверхности
конуса:О
А
В
К
3
5
О
Слайд 28
ЗАДАЧА 1
Дано: конус; R=3,l=5.
Найти: SБПК , Sппк.
Решение.
SБПК =
π*3*5=15 π;
Sосн = π*32 =9 π;
Sппк =15π+9π=24π.
О
А
В
К
3
5
О
Слайд 29
ЗАДАЧА 2.
По данным чертежа (ОВ=5,
КО=12) вычислите площадь боковой и площадь полной поверхности конуса:
А
О
В
К
5
12
Слайд 30
ЗАДАЧА 2.
Дано: конус; R=5, h=12.
Найти: SБПК , Sппк.
Решение.
l2=144+25=169,
l=13;
SБПК=π*13*5=65 π;
Sосн = π*52 =25 π;
Sппк =65π+25π;
Sппк =90π.О
В
К
5
12
А
Слайд 31
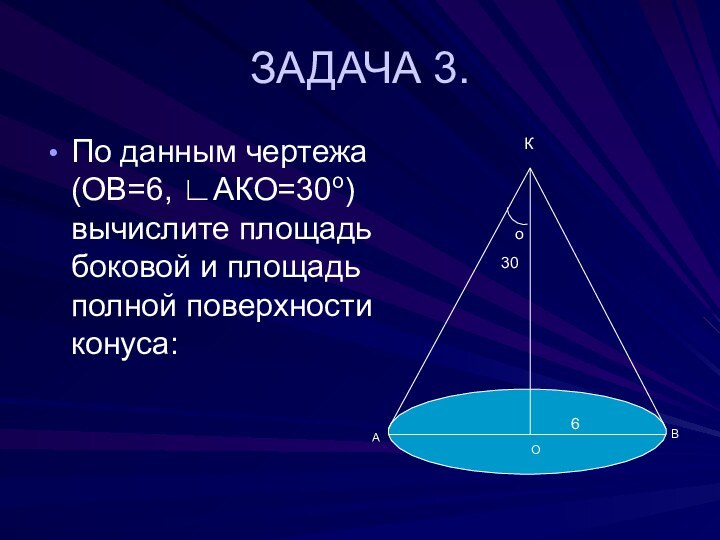
ЗАДАЧА 3.
По данным чертежа (ОВ=6,
∟АКО=30о) вычислите площадь боковой и площадь полной поверхности конуса:
о30
К
А
В
О
6
Слайд 32
ЗАДАЧА 3.
Дано: конус; R=6,∟АКО=30о.
Найти: SБПК , Sппк.
Решение.
l=R/sin30о,l=6/0.5=12;
SБПК=π*12*6=72π;
Sосн =
π*62 =36π;
Sппк =72π+36π; Sппк =108π.
о30
К
А
В
О
6
Слайд 33
ЗАДАЧА 4.
РАВНЫ ЛИ ПЛОЩАДИ ПОВЕРХНОСТЕЙ ДВУХ КОНУСОВ, ОБРАЗОВАННЫХ
ПРИ ВРАЩЕНИИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
ВОКРУГ КАТЕТОВ?А
В
С
А
В
С
С
В
С
Слайд 34
РЕШЕНИЕ ЗАДАЧИ 4
1) R=ВС= a ;
SППК 1= SБПК 1+ Sосн1=π a с+π a2 = π a (a + с).
2) R=АС= b ; SППК 2= SБПК 2+ Sосн2=π b с+π b2= π b (b + с).
Если SППК 1 = SППК 2, то a2 +aс = b2 +bc, a2-b2+ac - bc=0, (a-b)(a+b+c)=0. Т.к a,b,c – положительные числа (длины сторон треугольника), то равенство верно только в случае, если a = b.
Слайд 35
ДОМАШНЕЕ ЗАДАНИЕ:
УЧЕБНИК СТЕРЕОМЕТРИИ ПОД РЕД.
Л. С. АТАНАСЯНА -
п.55, 56; № 548, № 561.СПАСИБО ЗА ВНИМАНИЕ!