Слайд 2
1. Координатная ось
Координатной осью называется прямая, на которой

отмечена точка О (начало отсчета или начало координат), выбран
масштаб, т.е. указан отрезок единичной длины для измерения расстояний (единичный или масштабный отрезок), и задано положительное направление. Так на рисунке 1 единичный отрезок на координатной оси Ох обозначен OE, направление от точки О к точке Е считается положительным (показано стрелкой). Начало координат О делит координатную ось на два луча: положительную полуось (которой принадлежит точка Е)
и отрицательную полуось.
Координатой точки Р, лежащей на оси Ох, называется число х = ±ОР (где ОР означает длину отрезка ОР), взятое со знаком плюс, если точка Р лежит на положительной полуоси, и со знаком минус, если эта точка лежит на отрицательной полуоси. Координату точку обычно указывают в скобках рядом с обозначением точки: Р (х). Между точками на числовой оси и их координатами имеется взаимно однозначное соответствие. Расстояние между двумя точками Р1 (х1) и Р2(х2) на оси Ох выражается формулой т.е. оно равно модулю разности соответствующих координат.
Слайд 3
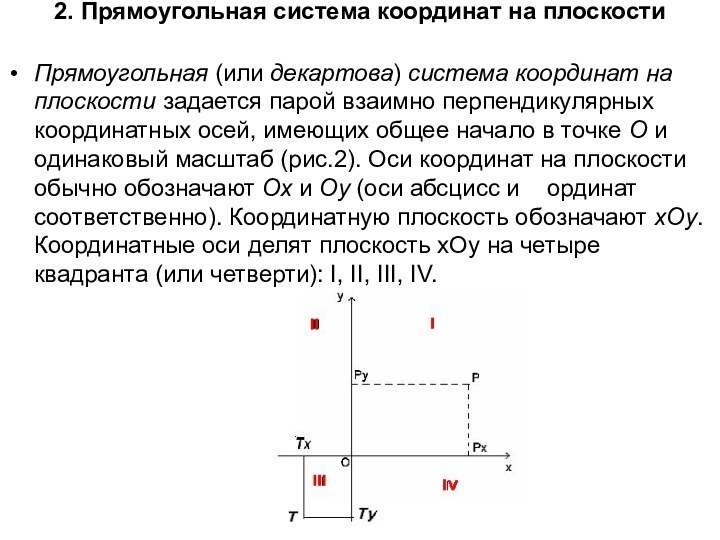
2. Прямоугольная система координат на плоскости
Прямоугольная (или декартова)
система координат на плоскости задается парой взаимно перпендикулярных координатных
осей, имеющих общее начало в точке О и одинаковый масштаб (рис.2). Оси координат на плоскости обычно обозначают Ох и Оу (оси абсцисс и ординат соответственно). Координатную плоскость обозначают хОу. Координатные оси делят плоскость хОу на четыре квадранта (или четверти): I, II, III, IV.
Слайд 4
Пусть точка Р лежит на плоскости хОу (рис.2).
Опустим из этой точки перпендикуляры на координатные оси; основания
перпендикуляров обозначим Рх и Ру.
Абсциссой точки Р называется координата х точки Рх на оси Ох,
ординатой – координата у точки Ру на оси Оу.
Координаты точки обычно указывают в скобках рядом с обозначением точки: Р (х; у). Между точками на плоскости и их координатами имеется взаимно однозначное соответствие.
Слайд 5
Рассмотрим пример
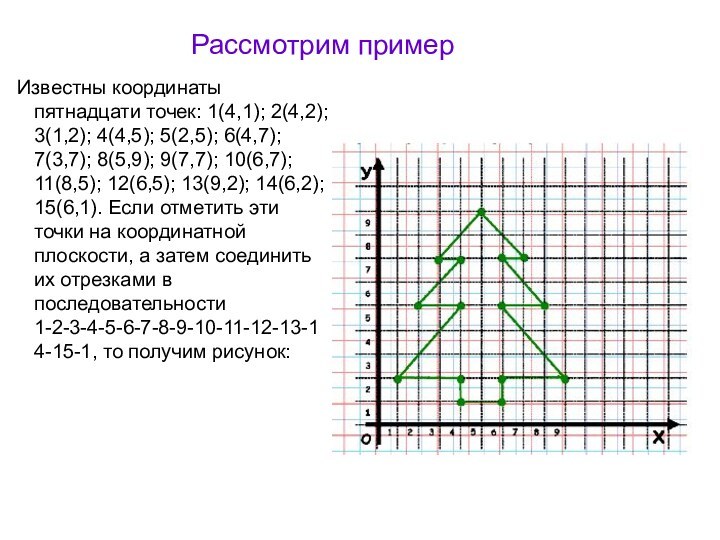
Известны координаты пятнадцати точек: 1(4,1); 2(4,2);
3(1,2); 4(4,5); 5(2,5); 6(4,7); 7(3,7); 8(5,9); 9(7,7); 10(6,7); 11(8,5);
12(6,5); 13(9,2); 14(6,2); 15(6,1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности 1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-1, то получим рисунок:
Слайд 6
Задача 1
Даны точки A(0; - 2), B(- 2;1),
C(0;0) и D(2; - 9). Укажите те из них,
которые лежат на прямой 2x - 3y + 7 = 0.
Решение
Уравнению прямой удовлетворяют координаты только точки B, т.к.
2(-2)- 3(1)+7=0, -4-3+7=0, 0=0
Слайд 7
3. Расстояние между точками
Пусть на плоскости хОу даны
две точки: A1с координатами(x1;y1;) , и A2 с координатами(x2;y2)
, . Выразим расстояние между точками и А через координаты этих точек. Рис.3
Рассмотрим сначала случай, когда х ≠ х1 и у ≠ у1. Проведем через точки А и А2прямые, параллельные осям координат , и обозначим точку их пересечения буквой А (рис.3). Расстояние между точками А и А 1 равно ׀у2-у 1 ׀, а расстояние между точками А и А 2 равно ׀х1-х 2 ׀. Применяя к прямоугольному треугольнику АА1А2 теорему Пифагора, получим:
, откуда
1) ,
где d – расстояние между
точками А и А.
Слайд 8
Хотя формула (1) для расстояния между точками выведена
нами в предположении х ≠ х1, у ≠ у
1, она остается верной и в других случаях. Действительно, если х = х 1, у ≠ у 1, то d равно ׀у – у 1 ׀. Тот же результат дает формула (1). Аналогично рассматривается случай, когда х ≠ х 1,
у = у 1. При х = х 1, у = у 1 точки А и А 1 совпадают и формула (1) дает d = 0.
Слайд 9
Задача 2
Даны точки A(0;0), B(- 2;1), C(3;3), D(2;
- 1) и окружность (x - 1)2 + (y
+ 3)2 = 25. Выясните, где расположены эти точки: на окружности, внутри или вне окружности.
Решение
Подставив координаты данных точек в левую часть уравнения данной окружности, найдём квадраты расстояний от данных точек до центра Q(1; - 3) окружности:
QA2 = (0 - 1) 2 + (0 + 3) 2 = 10 < 25,
QB2 = (- 2 - 1) 2 + (1 + 3) 2 = 25,
QC2 = (3 - 1) 2 + (3 + 3) 2 = 40 > 25,
QD2 = (2 - 1) 2 + (- 1 + 3) 2 = 5 < 25.
Следовательно, точки A и D расположены внутри окружности, точка B — на окружности, а точка C — вне окружности.
Слайд 10
Задача 3
Найти расстояние между точками
А (-1; -2)
и В (-4; 2).
Решение. По формуле (1) имеем:
Слайд 11
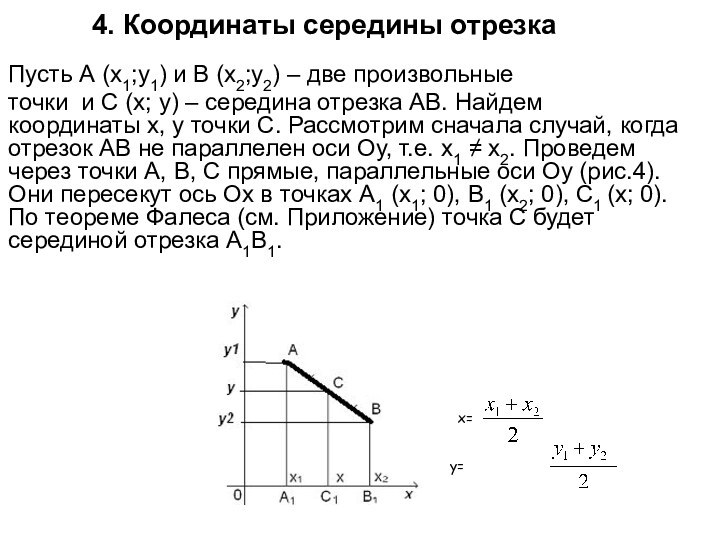
4. Координаты середины отрезка
Пусть А (х1;у1) и В
(х2;у2) – две произвольные
точки и С (х; у)
– середина отрезка АВ. Найдем координаты х, у точки С. Рассмотрим сначала случай, когда отрезок АВ не параллелен оси Оу, т.е. х1 ≠ х2. Проведем через точки А, В, С прямые, параллельные оси Оу (рис.4). Они пересекут ось Ох в точках А1 (х1; 0), В1 (х2; 0), С1 (х; 0). По теореме Фалеса (см. Приложение) точка С будет серединой отрезка А1В1.
x=
y=
Слайд 12
Найдем координаты х, у точки С. Рассмотрим сначала
случай, когда отрезок АВ не параллелен оси Оу, т.е.
х ≠ х. Проведем через точки А, В, С прямые, параллельные оси Оу (рис.4). Они пересекут ось Ох в точках А1 (х1; 0), В1 (х2; 0), С1 (х; 0). По теореме Фалеса (см. Приложение 7) точка С1 будет серединой отрезка А1В1.
Так как точка С1 – середина отрезка А1В1, то А1С1 = С1В1. при выбранном расположении точек имеем:
А1С1 = х – х1, С1В1 = х – х1 И, значит, х – х1= х – х2, откуда 2)
Аналогично получим: 3)
Слайд 14
Задача 4
Даны две вершины параллелограмма АВСD: А (0;
1) , С (3; 2). Найти координаты точки пересечения
диагоналей.
Решение. Точка пересечения диагоналей является серединой отрезка АС и имеет координаты:
Слайд 15
Задача 5
Даны точки A(- 6; - 1), B(1;2)
и C(- 3; - 2). Найдите координаты вершины M
параллелограмма ABMC
Решение.. Первый способ
Координаты середины K(x0;y0) диагонали BC параллелограмма ABMC есть средние арифметические соответствующих координат концов отрезка BC, т.е.
x0 = = - 1, y0 = = 0.
Поскольку диагонали параллелограмма делятся точкой пересечения пополам, то K(x0;y0) — середина отрезка с концами в точках A(- 6; - 1) и M(x1;y1). Поэтому x0 = = - 1, y0 = = 0.
Отсюда находим, что x1 = 4, y1 = 1.
Второй способ..
Пусть x1, y1 — координаты точки M. Если ABMC — параллелограмм, то , а т.к. то x1 - 1 = 3, y1 - 2 = - 1.
Отсюда находим, что x1 = 4, y1 = 1.
Ответ: M(4;1).
Слайд 16
5. Определение тригонометрических функций для любого угла от
0° до 180°
До сих пор значение синуса, косинуса и
тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. Возьмем окружность на плоскости хОу с центром в начале координат и радиусом R (рис.6). Пусть α – острый угол, который образует радиус ОА с положительной полуосью Ох. Пусть х и у – координаты точки А. Значение sin α и tg α для острого угла α выражаются через координаты точки А, а именно:
sinα = , cosα = , tgα =
Слайд 17
Определим теперь значения sin α, cos α и
tg α для любого угла α. (Для tg α
угол α = 90° исключается).
Имеем: sin 90° = = 1, cos90° = = 0, sin180° = 0, cos180° =- = -1
Считая, что совпадающие лучи образуют угол 0°, будем иметь:
sin0° = 0, cos0° = 1, tg0° = 0
Теорема:
Для любого угла α, 0° < α < 180°,
sin (180° - α) = sin α,
cos (180° - α) = -cos α
Для угла α ≠ 90°
tg (180° - α) = -tg α
Слайд 18
Задача 6
Вычислить: 1) sin 135°; 2) cos
135°; 3) 150°
Решение. Согласно только что доказанной теореме
sin 135° = sin (180°- 45°) = sin 45°;
cos 135° = cos (180° - α) = -cos 45°;
tg 150° = tg (180° - α) = -tg 30°
Но sin 45° = √2/2, cos 45° = √2/2 , tg 30° = √3/3
Следовательно, sin 135° = √2/2,
cos 135° = - √2/2, tg 135° = - √3/3
Слайд 19
6. Применение координатной плоскости при решении алгебраических задач
Задача
7
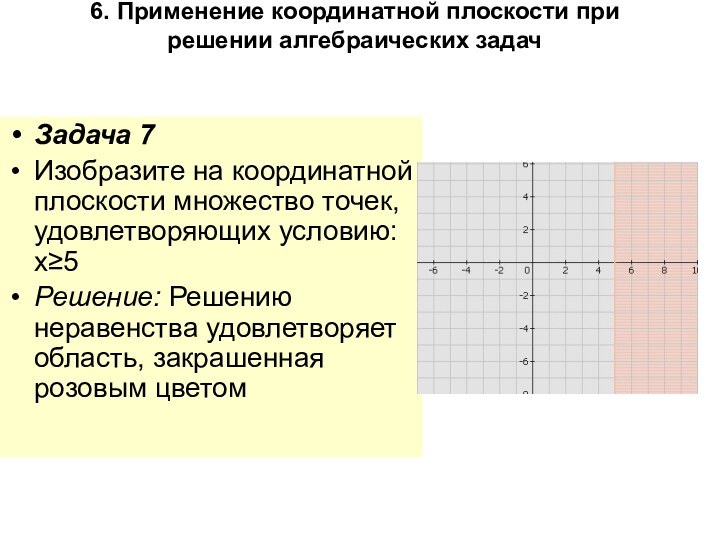
Изобразите на координатной плоскости множество точек, удовлетворяющих условию: х≥5
Решение:
Решению неравенства удовлетворяет область, закрашенная розовым цветом
Слайд 20
Задача 8
Покажите на координатной плоскости множество точек, которое
задается неравенством
Решение:
Множество точек плоскости, удовлетворяющих данному неравенству, выделено
на рисунке 8 серым цветом.
Слайд 21
Задача 9
На рисунке изображено некоторое множество точек. Из
двух неравенств выберете то, которому оно соответствует
и .
Решение
Множество точек изображенных на рисунке СЕРЫМ ЦВЕТОМ , соответсвует неравенству
Слайд 22
Задача 10
Постройте какую-нибудь полосу, охватывающую все данные точки
на рисунке 10. Каким неравенством ее
можно задать?
Решение:
Решение данной
задачи можно увидеть на рис.11, это область образованная пересечением двух областей желтого и синего цвета. Получившуюся область можно задать неравенством -9≤у≤10
Слайд 23
7. Применение координатной плоскости при решении геометрических задач
Задача
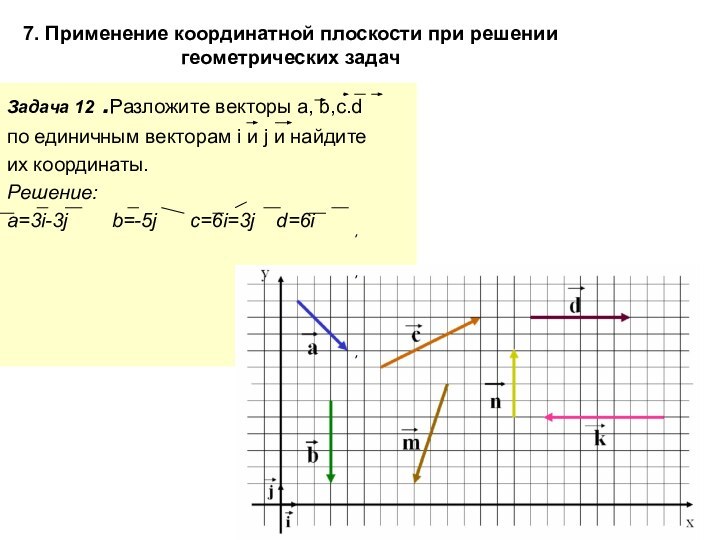
12 .Разложите векторы а, b,c.d
по единичным векторам i и
j и найдите
их координаты.
Решение:
a=3i-3j b=-5j c=6i=3j d=6i
,
,
,
Слайд 24
Задача 11
Решить графически систему уравнений
Решение:Графиком уравнения х2+у2=25
является окружность
с центром в начале координат и радиусом, Равным5.
Графиком уравнения
ху=12 является Гипербола у=12:х. Построив графики в одной системе координат (рис.11), найдём координаты точек А, В, С, Д пересечения окружности и гиперболы: А(4; 3), В(3; 4), С(-4; -3), Д(-3; -4). Значит, решения заданной системы таковы: (4;3), (3;4), (-4;-3), (-3; -4).
Слайд 25
Задача 13
На координатной плоскости заданы точки A(1;3), B(1;9),
C(6;8) и E(5;1). Найдите площадь пятиугольника ABCDE, где D
— точка пересечения прямых AC и BE.
Решение
Если y1y2 и x1x2, то уравнение прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид =
Ответ:21
Слайд 26
Задача 14
На координатной
плоскости (x;y)
проведена окружность
радиуса 4 с центром
в
начале координат.
Прямая, заданная
уравнением y = 4 - (2 -
)x,
пересекает её в точках A
и B. Найдите сумму длин отрезка AB и меньшей дуги AB.
Слайд 27
Решение
Решив систему уравнений
Найдем координаты точек пересечения прямой
и окружности: А(0;4), В(2,2;).
Тогда, АВ =
Пусть О-
начало координат. По теореме
косинусов из треугольника АОB находим, что
cos∕AOB= .
Поэтому градусная мера меньшей дуги АВ
равна 300.Длина этой дуги равна одной
двенадцатой длины окружности радиуса 4, т.е. . . Следовательно, искомая сумма равна
+4 Ответ: +4
.
Слайд 28
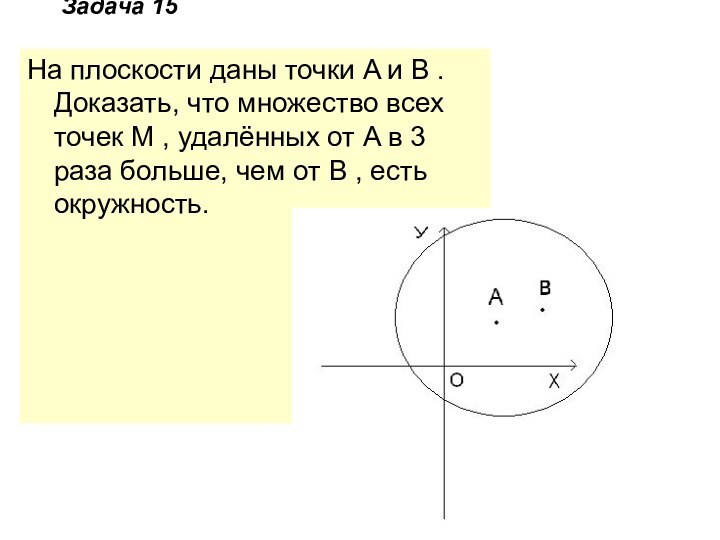
Задача 15
На плоскости даны точки A и B
. Доказать, что множество всех точек M , удалённых
от A в 3 раза больше, чем от B , есть окружность.
Слайд 29
Решение
Решим задачу координатным методом. Введём систему
координат таким образом,
чтобы A находилась в начале
координат, а B имела координаты
(1;0) . Пусть точка
M(x,y) – искомая. Тогда 1/3=MB/MA= .
Отсюда получаем x2+y2=9((x-1) 2+y2 ,
8x2-18x+8(x- ) 2+y2( )2- .
Получили уравнение окружности. Следовательно, все
точки M данного множества лежат на окружности. Далее,
так как все наши преобразования были равносильными, то любая точка, лежащая на окружности, заданной получившимся уравнением, будет принадлежать данному множеству.
y2+9=0 ,
x2- x+y2+ =0; x2-2· x+( )2+y2+ -( )2=0;