Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Виды движения тел

Содержание

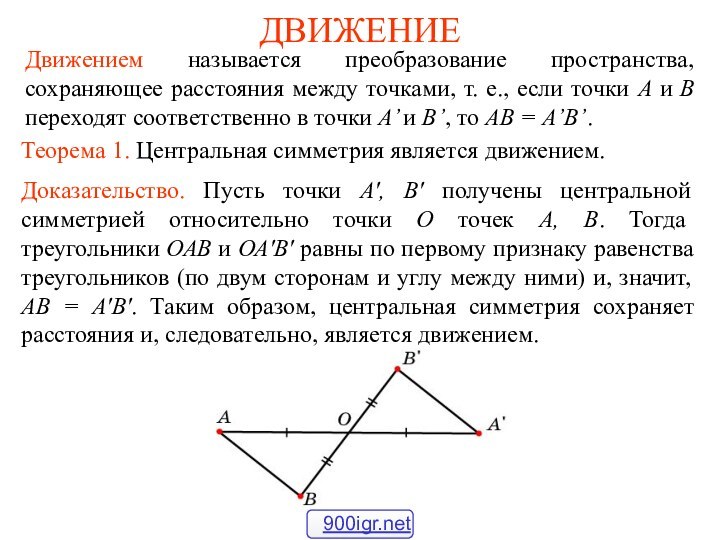
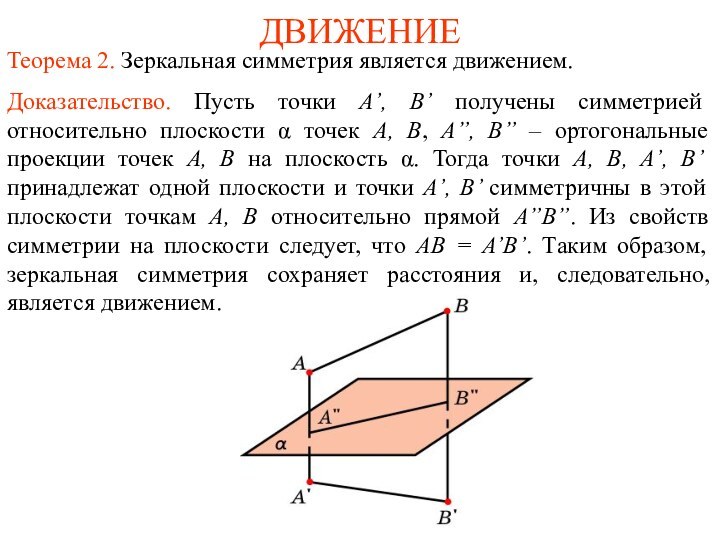
2. ДВИЖЕНИЕТеорема 2. Зеркальная симметрия является движением.Доказательство. Пусть
3. Упражнение 1Назовите движение, которое оставляет на месте
4. Упражнение 2Существуют ли движения (если существуют, то
5. Упражнение 3С помощью каких движений можно перевести
6. Упражнение 4Существует ли движение (если существует, то
7. Упражнение 5В правильном тетраэдре закрасили одну грань.
8. Упражнение 6Сколько существует различных движений, переводящих правильный тетраэдр в себя?Ответ: 24.
9. Упражнение 7Существует ли движение (если существует, то
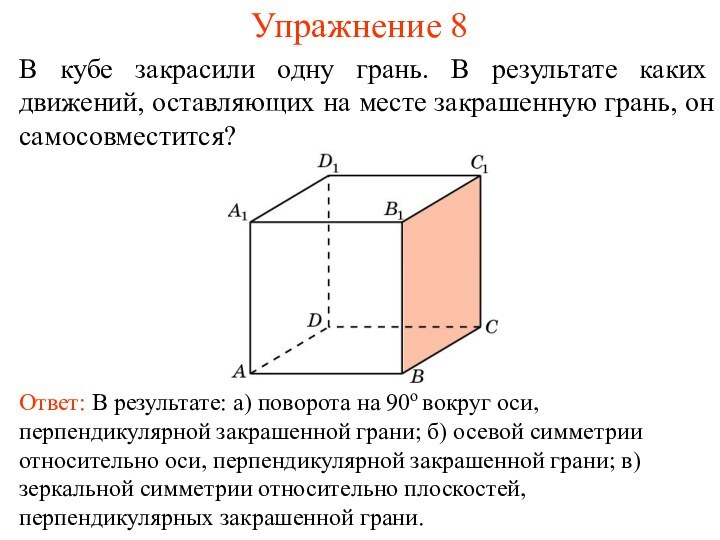
10. Упражнение 8В кубе закрасили одну грань. В
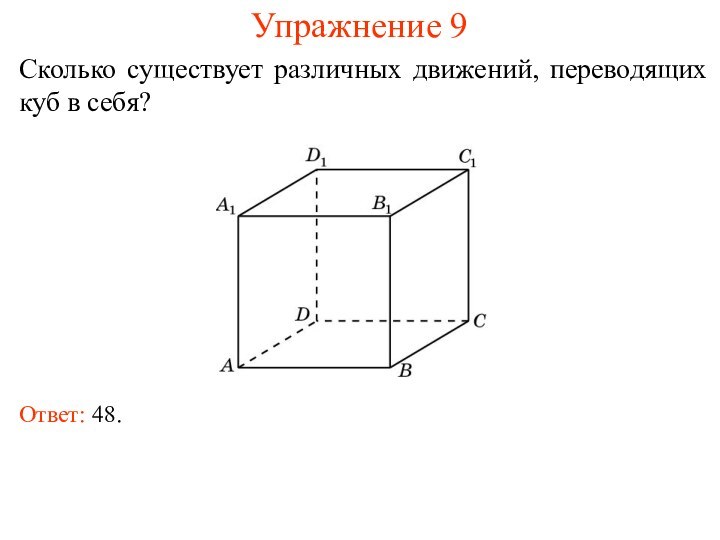
11. Упражнение 9Сколько существует различных движений, переводящих куб в себя?Ответ: 48.
12. Скачать презентацию
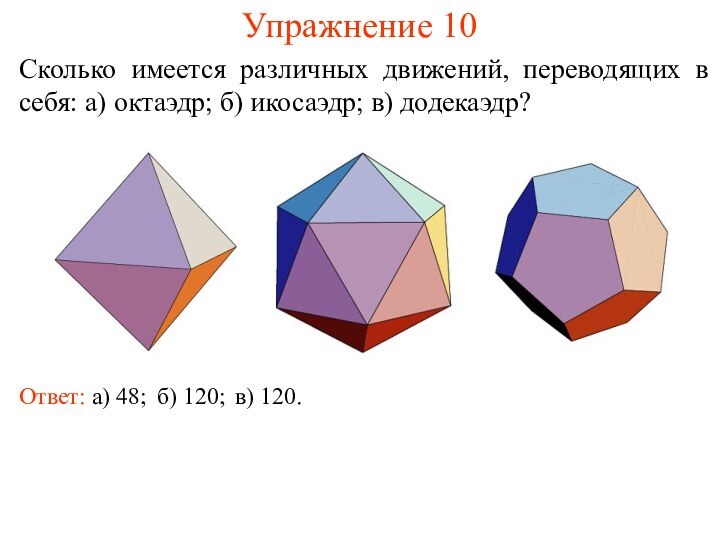
13. Похожие презентации

ДВИЖЕНИЕТеорема 2. Зеркальная симметрия является движением.Доказательство. Пусть точки A’, B’ получены симметрией относительно плоскости α точек A, B, A”, B” – ортогональные проекции точек A, B на плоскость α. Тогда точки A, B, A’, B’ принадлежат

ДВИЖЕНИЕДвижением называется преобразование пространства, сохраняющее расстояния между точками, т. е., если точки

Упражнение 1Назовите движение, которое оставляет на месте только: а) одну точку; б)

Упражнение 2Существуют ли движения (если существуют, то какие), переводящие данную прямую в

Упражнение 3С помощью каких движений можно перевести грань ABC правильного тетраэдра ABCD

Упражнение 4Существует ли движение (если существует, то какое), переводящее вершины A, B,

Упражнение 5В правильном тетраэдре закрасили одну грань. В результате каких движений, оставляющих

Упражнение 6Сколько существует различных движений, переводящих правильный тетраэдр в себя?Ответ: 24.

Упражнение 7Существует ли движение (если существует, то какое), переводящее вершины A, B,

Упражнение 8В кубе закрасили одну грань. В результате каких движений, оставляющих на

Упражнение 9Сколько существует различных движений, переводящих куб в себя?Ответ: 48.

Упражнение 10Сколько имеется различных движений, переводящих в себя: а) октаэдр; б) икосаэдр;

Слайды презентации

Слайд 2 ДВИЖЕНИЕ
Теорема 2. Зеркальная симметрия является движением.
Доказательство. Пусть точки

ДВИЖЕНИЕТеорема 2. Зеркальная симметрия является движением.Доказательство. Пусть точки A’, B’ получены

A’, B’ получены симметрией относительно плоскости α точек A,

B, A”, B” – ортогональные проекции точек A, B на плоскость α. Тогда точки A, B, A’, B’ принадлежат одной плоскости и точки A’, B’ симметричны в этой плоскости точкам A, B относительно прямой A”B”. Из свойств симметрии на плоскости следует, что AB = A’B’. Таким образом, зеркальная симметрия сохраняет расстояния и, следовательно, является движением.

Слайд 3 Упражнение 1
Назовите движение, которое оставляет на месте только:

Упражнение 1Назовите движение, которое оставляет на месте только: а) одну точку;

а) одну точку; б) точки одной прямой; в) точки

одной плоскости.

Ответ: а) Центральная симметрия;

б) осевая симметрия;

в) зеркальная симметрия.

Слайд 4 Упражнение 2
Существуют ли движения (если существуют, то какие),

Упражнение 2Существуют ли движения (если существуют, то какие), переводящие данную прямую

переводящие данную прямую в другую данную прямую: а) параллельную

первой; б) пересекающую первую; в) скрещивающуюся с первой?

Ответ: а) Центральная симметрия, зеркальная симметрия, параллельный перенос;

б) осевая симметрия, поворот, зеркальная симметрия;

в) осевая симметрия.

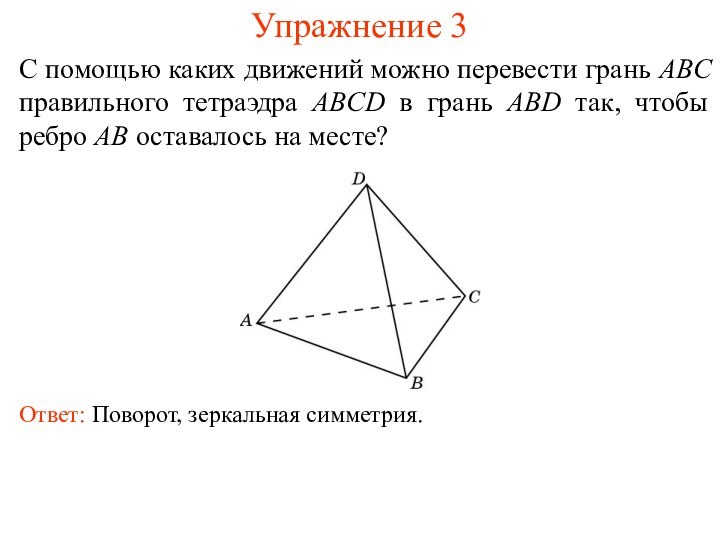
Слайд 5 Упражнение 3
С помощью каких движений можно перевести грань

Упражнение 3С помощью каких движений можно перевести грань ABC правильного тетраэдра

ABC правильного тетраэдра ABCD в грань ABD так, чтобы

ребро AB оставалось на месте?

Ответ: Поворот, зеркальная симметрия.

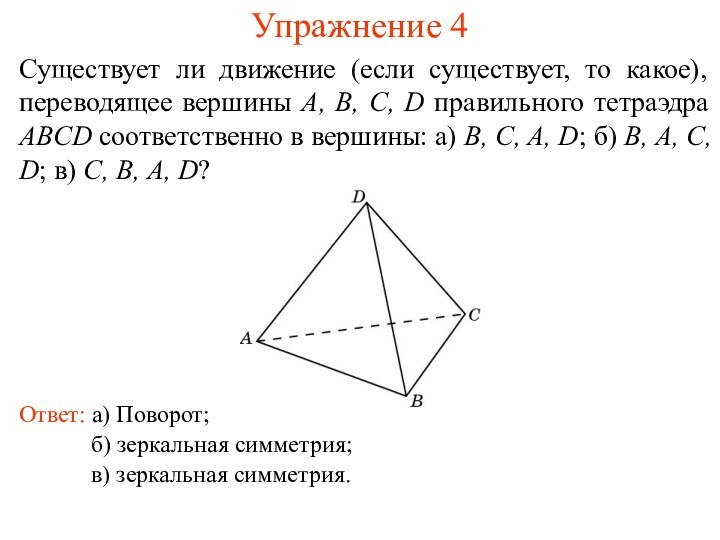
Слайд 6 Упражнение 4
Существует ли движение (если существует, то какое),

Упражнение 4Существует ли движение (если существует, то какое), переводящее вершины A,

переводящее вершины A, B, C, D правильного тетраэдра ABCD

соответственно в вершины: а) B, C, A, D; б) B, A, C, D; в) C, B, A, D?

Ответ: а) Поворот;

б) зеркальная симметрия;

в) зеркальная симметрия.

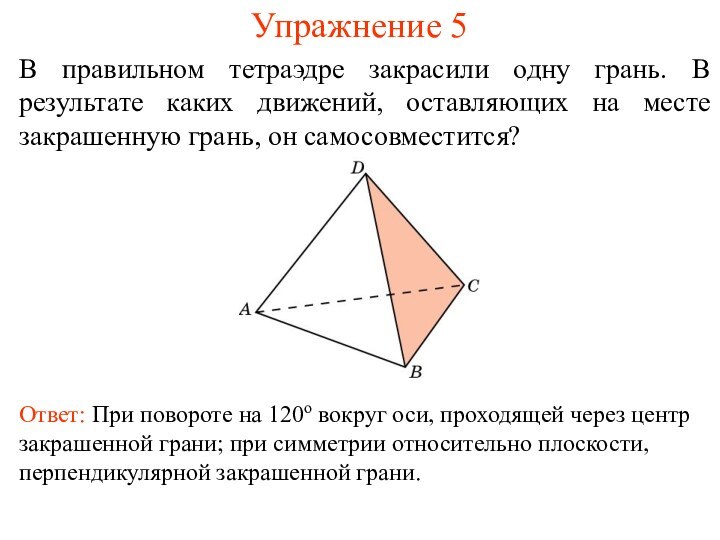
Слайд 7 Упражнение 5
В правильном тетраэдре закрасили одну грань. В

Упражнение 5В правильном тетраэдре закрасили одну грань. В результате каких движений,

результате каких движений, оставляющих на месте закрашенную грань, он

самосовместится?

Ответ: При повороте на 120о вокруг оси, проходящей через центр закрашенной грани; при симметрии относительно плоскости, перпендикулярной закрашенной грани.

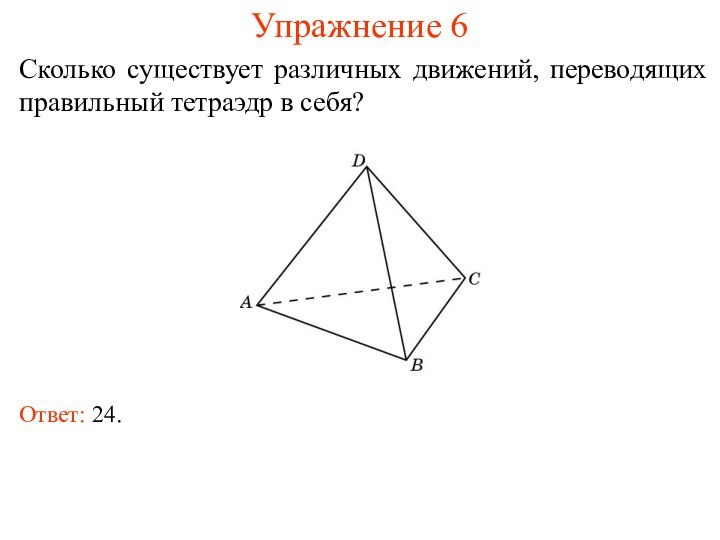
Слайд 8 Упражнение 6
Сколько существует различных движений, переводящих правильный тетраэдр

в себя?
Ответ: 24.

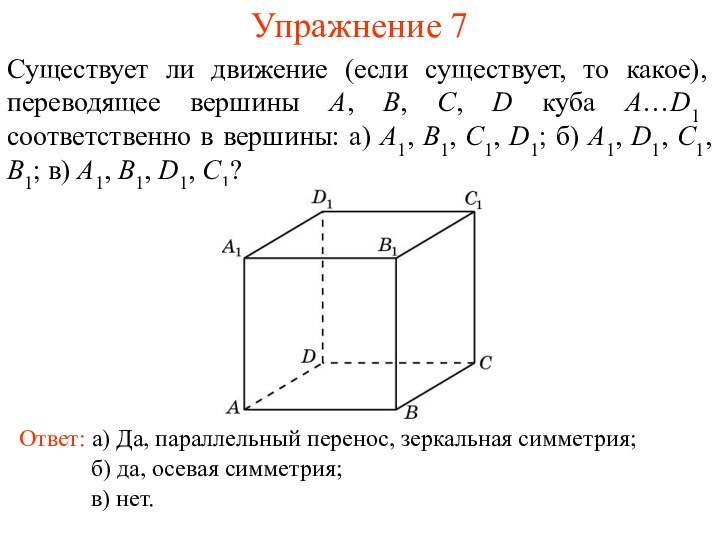
Слайд 9 Упражнение 7
Существует ли движение (если существует, то какое),

Упражнение 7Существует ли движение (если существует, то какое), переводящее вершины A,

переводящее вершины A, B, C, D куба A…D1 соответственно

в вершины: а) A1, B1, C1, D1; б) A1, D1, C1, B1; в) A1, B1, D1, C1?

Ответ: а) Да, параллельный перенос, зеркальная симметрия;

б) да, осевая симметрия;

в) нет.

Слайд 10 Упражнение 8
В кубе закрасили одну грань. В результате

Упражнение 8В кубе закрасили одну грань. В результате каких движений, оставляющих

каких движений, оставляющих на месте закрашенную грань, он самосовместится?
Ответ:

В результате: а) поворота на 90о вокруг оси, перпендикулярной закрашенной грани; б) осевой симметрии относительно оси, перпендикулярной закрашенной грани; в) зеркальной симметрии относительно плоскостей, перпендикулярных закрашенной грани.