Слайд 2
Правильные многоугольники
Выпуклый многоугольник называется правильным, если у него
все стороны равны и все углы равны.
Центром правильного
многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Слайд 3
Свойства правильного многоугольника:
Правильный многоугольник является вписанным в окружность
и описанным около окружности.
Центр правильного многоугольника совпадает с
центрами вписанной и описанной окружностей.
Периметры правильных n-угольников относятся как радиусы описанных окружностей.
Слайд 4
Виды правильных многоугольников.
Слайд 5
Правильные многогранники
«Правильных многогранников вызывающе мало, – написал когда-то
Л. Кэрролл – но этот весьма скромный по численности
отряд сумел пробраться в самые глубины различных наук».
Слайд 6
Многогранник- это такое тело, поверхность которого состоит из
конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он
расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности.
Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками.
Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника.
Слайд 7
Существует 5 видов правильных многогранников:
1)тетраэдр
2) гексаэдр
3) додекаэдр
4)октаэдр
5)икосаэдр
Слайд 8
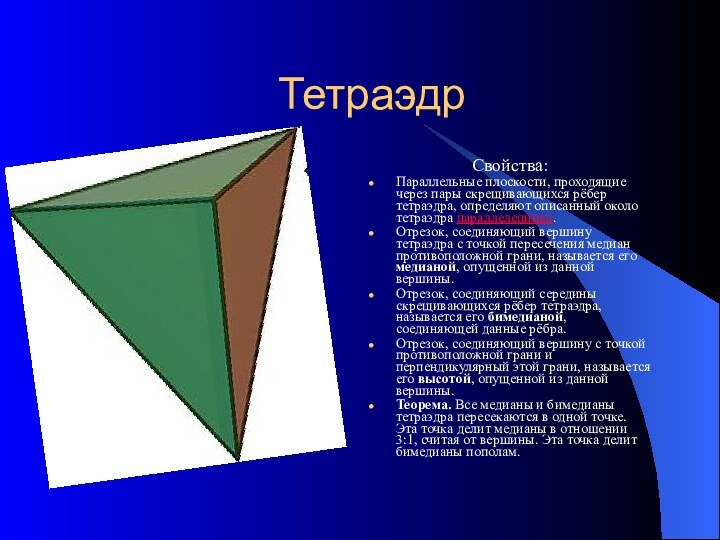
Тетраэдр
Свойства:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра,
определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с
точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Слайд 9
Гексаэдр
Свойства :
Четыре сечения куба являются правильными шестиугольниками —
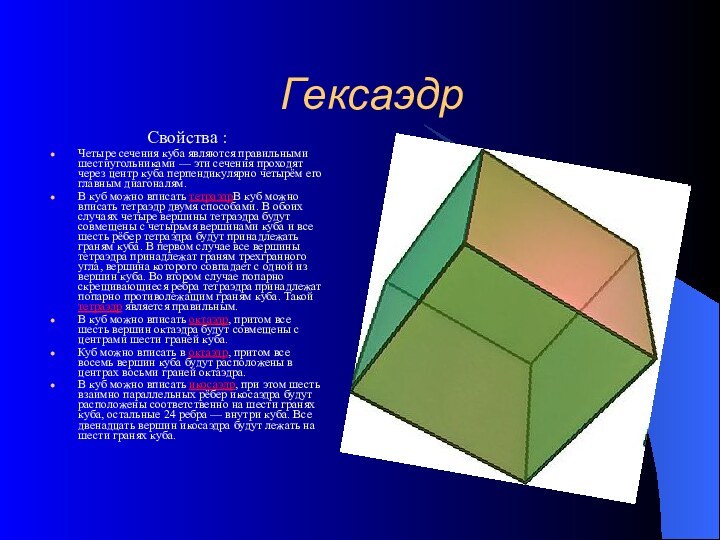
эти сечения проходят через центр куба перпендикулярно четырём его
главным диагоналям.
В куб можно вписать тетраэдрВ куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Слайд 10
Додекаэдр
(от греческого dodeka – двенадцать и hedra –
грань) Правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр
имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.
Слайд 11
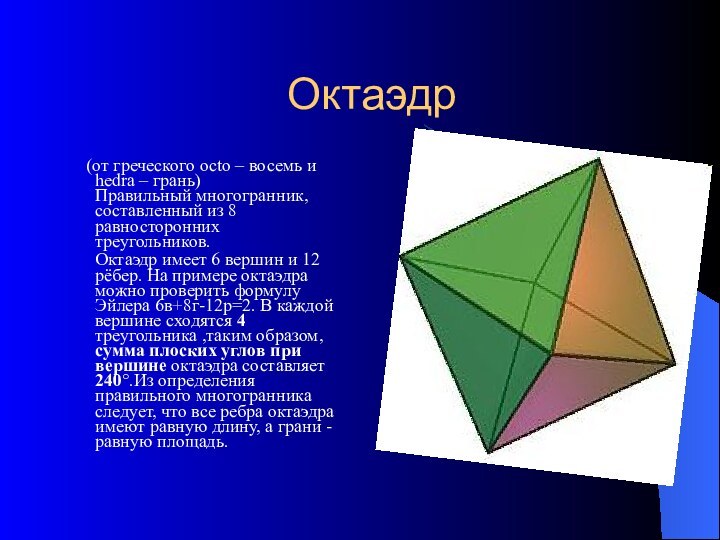
Октаэдр
(от греческого octo – восемь и
hedra – грань)
Правильный многогранник, составленный из 8 равносторонних треугольников.
Октаэдр имеет 6 вершин и 12 рёбер. На примере октаэдра можно проверить формулу Эйлера 6в+8г-12р=2. В каждой вершине сходятся 4 треугольника ,таким образом, сумма плоских углов при вершине октаэдра составляет 240°.Из определения правильного многогранника следует, что все ребра октаэдра имеют равную длину, а грани - равную площадь.
Слайд 12
Икосаэдр
Свойства:
Икосаэдр можно вписать в куб, при этом, шесть
взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести
гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.