- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Многогранный угол
Содержание
- 2. МНОГОГРАННЫЕ УГЛЫ В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.
- 3. ТРЕХГРАННЫЕ УГЛЫ Теорема. Всякий плоский угол трехгранного угла
- 4. ТРЕХГРАННЫЕ УГЛЫ Свойство. Сумма плоских углов трехгранного угла
- 5. ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫМногогранный угол называется выпуклым, если
- 6. Вертикальные многогранные углы На рисунках приведены примеры трехгранных, четырехгранных и пятигранных вертикальных углов Теорема. Вертикальные углы равны.
- 7. Измерение многогранных углов Поскольку градусная величина развернутого двугранного
- 8. Измерение трехгранных углов*Выведем формулу, выражающую величину трехгранного
- 9. Измерение многогранных углов*Пусть SA1…An – выпуклый n-гранный
- 10. Упражнение 1Может ли быть трехгранный угол с
- 11. Упражнение 2Приведите примеры многогранников, у которых грани,
- 12. Упражнение 3Два плоских угла трехгранного угла равны
- 13. Упражнение 4Плоские углы трехгранного угла равны 45°,
- 14. Упражнение 5В трехгранном угле два плоских угла
- 15. Упражнение 6Плоские углы трехгранного угла равны 60°,
- 16. Упражнение 7Каждый плоский угол трехгранного угла равен
- 17. Упражнение 8Найдите геометрическое место внутренних точек трехгранного
- 18. Упражнение 9Найдите геометрическое место внутренних точек трехгранного
- 19. Упражнение 10 Найдите приближенные значения трехгранных углов тетраэдра.
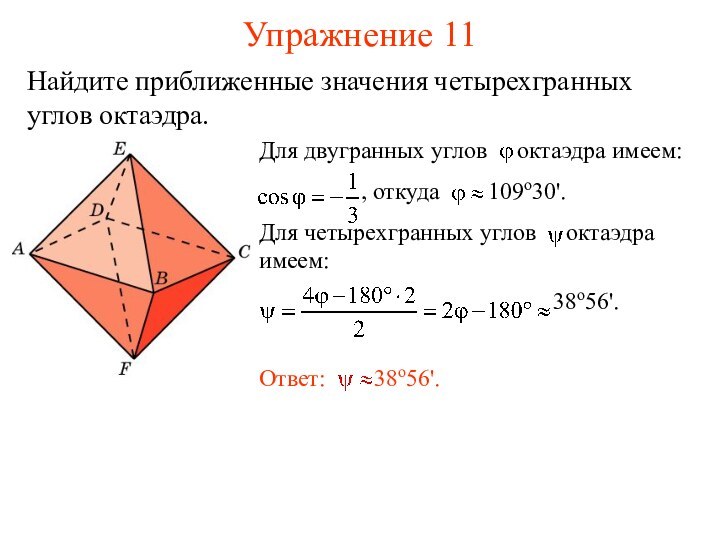
- 20. Упражнение 11Найдите приближенные значения четырехгранных углов октаэдра.
- 21. Упражнение 12Найдите приближенные значения пятигранных углов икосаэдра.
- 22. Упражнение 13Найдите приближенные значения трехгранных углов додекаэдра.
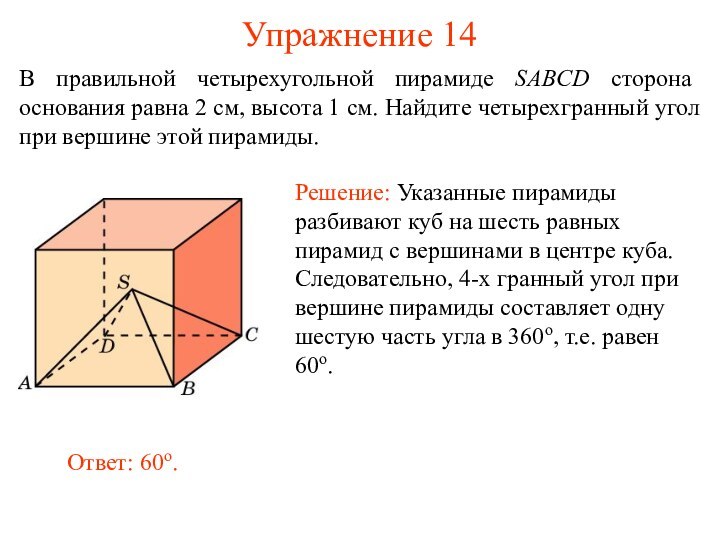
- 23. Упражнение 14В правильной четырехугольной пирамиде SABCD сторона
- 24. Упражнение 15В правильной треугольной пирамиде боковые ребра
- 25. Скачать презентацию
- 26. Похожие презентации


















Слайд 2
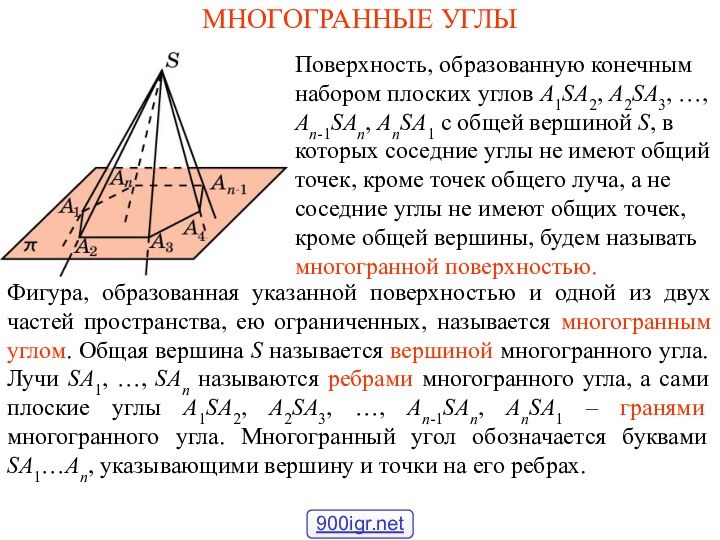
МНОГОГРАННЫЕ УГЛЫ
В зависимости от числа граней многогранные углы
бывают трехгранными, четырехгранными, пятигранными и т. д.
Слайд 3
ТРЕХГРАННЫЕ УГЛЫ
Теорема. Всякий плоский угол трехгранного угла меньше
суммы двух других его плоских углов.
Доказательство. Рассмотрим трехгранный угол
SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства ∠ASB ≤ ∠ASC < ∠ASC + ∠BSC; ∠BSC ≤ ∠ASC < ∠ASC + ∠ASB.Таким образом, остается доказать неравенство ∠ASС < ∠ASB + ∠BSC.
Воспользуемся неравенством треугольника AC < AB + BC. Вычитая из обеих его частей AD = AB, получим неравенство DC < BC. В треугольниках DSC и BSC одна сторона общая (SC), SD = SB и DC < BC. В этом случае против большей стороны лежит больший угол и, следовательно, ∠DSC < ∠BSC. Прибавляя к обеим частям этого неравенства угол ASD, равный углу ASB, получим требуемое неравенство ∠ASС < ∠ASB + ∠BSC.
Отложим на грани ASC угол ASD, равный ASB, и точку B выберем так, чтобы SB = SD. Тогда треугольники ASB и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB = AD.
Слайд 4
ТРЕХГРАННЫЕ УГЛЫ
Свойство. Сумма плоских углов трехгранного угла меньше
360°.
Аналогично, для трехгранных углов с вершинами B и С
имеют место неравенства: ∠ ABС < ∠ ABS + ∠ CBS, ∠ ACB < ∠ ACS + ∠BCS. Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем 180°< ∠ BAS + ∠ CAS + ∠ ABS + ∠ CBS + ∠ BCS + ∠ ACS = 180° - ∠ ASB + 180° - ∠ BSC + 180° - ∠ ASC. Следовательно, ∠ ASB + ∠ BSC + ∠ ASC < 360° . Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу доказанного свойства, имеет место неравенство ∠ BAС < ∠BAS + ∠ CAS.
Слайд 5
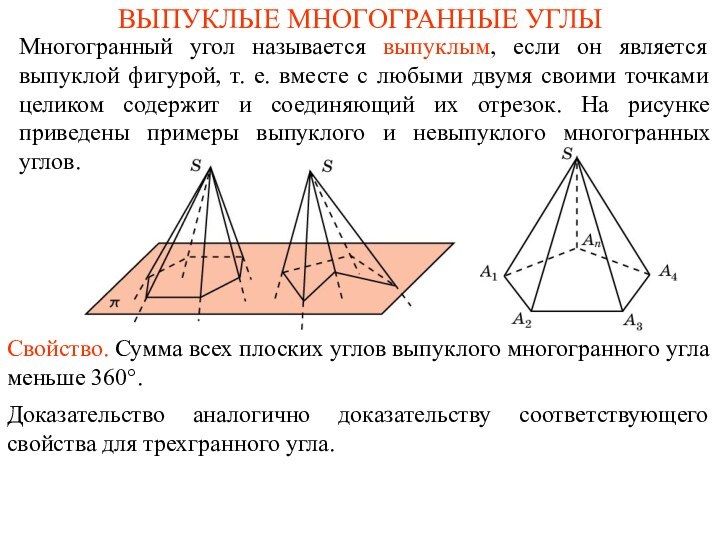
ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫ
Многогранный угол называется выпуклым, если он
является выпуклой фигурой, т. е. вместе с любыми двумя
своими точками целиком содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов.Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°.
Доказательство аналогично доказательству соответствующего свойства для трехгранного угла.
Слайд 6
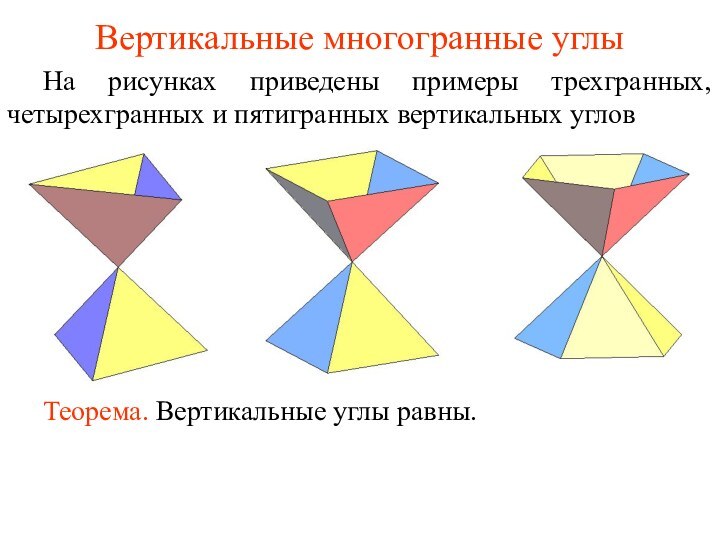
Вертикальные многогранные углы
На рисунках приведены примеры трехгранных, четырехгранных
и пятигранных вертикальных углов
Теорема. Вертикальные углы равны.
Слайд 7
Измерение многогранных углов
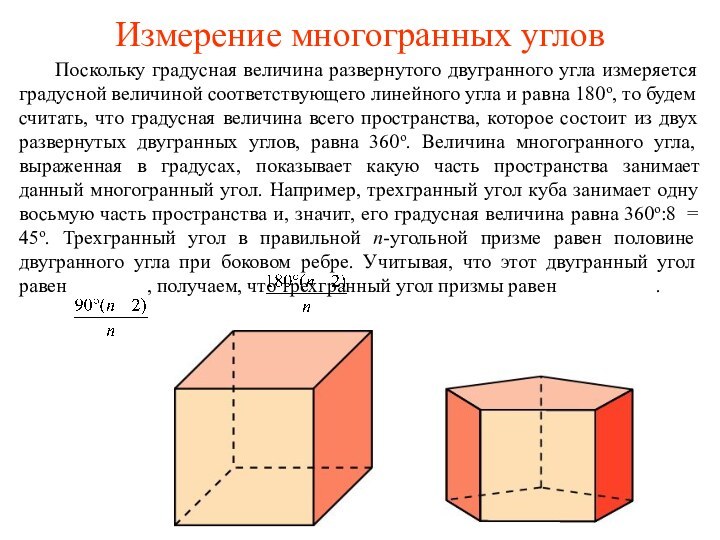
Поскольку градусная величина развернутого двугранного угла
измеряется градусной величиной соответствующего линейного угла и равна 180о,
то будем считать, что градусная величина всего пространства, которое состоит из двух развернутых двугранных углов, равна 360о. Величина многогранного угла, выраженная в градусах, показывает какую часть пространства занимает данный многогранный угол. Например, трехгранный угол куба занимает одну восьмую часть пространства и, значит, его градусная величина равна 360о:8 = 45о. Трехгранный угол в правильной n-угольной призме равен половине двугранного угла при боковом ребре. Учитывая, что этот двугранный угол равен , получаем, что трехгранный угол призмы равен .
Слайд 8
Измерение трехгранных углов*
Выведем формулу, выражающую величину трехгранного угла
через его двугранные углы. Опишем около вершины S трехгранного
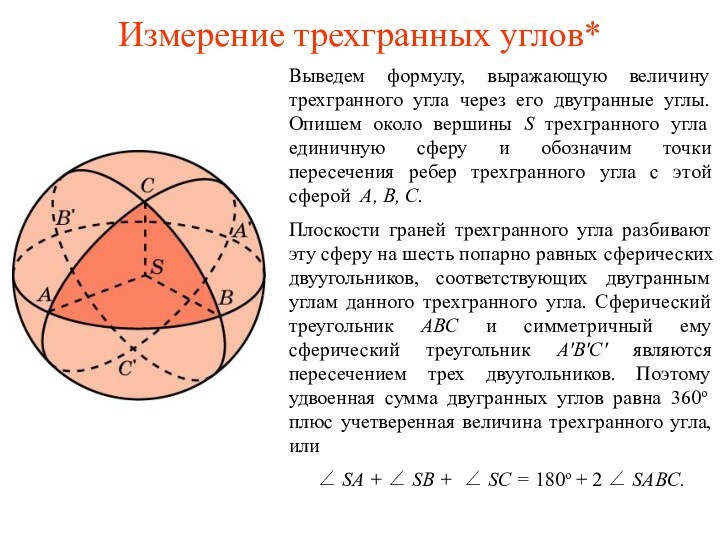
угла единичную сферу и обозначим точки пересечения ребер трехгранного угла с этой сферой A, B, C.Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360о плюс учетверенная величина трехгранного угла, или
∠ SA + ∠ SB + ∠ SC = 180о + 2 ∠ SABC.
Слайд 9
Измерение многогранных углов*
Пусть SA1…An – выпуклый n-гранный угол.
Разбивая его на трехгранные углы, проведением диагоналей A1A3, …,
A1An-1 и применяя к ним полученную формулу, будем иметь:∠ SA1 + … + ∠ SAn = 180о(n – 2) + 2 ∠ SA1…An.
Многогранные углы можно измерять и числами. Действительно, тремстам шестидесяти градусам всего пространства соответствует число 2π. Переходя от градусов к числам в полученной формуле, будем иметь:
∠SA1+ …+∠SAn = π (n – 2) + 2∠SA1…An.
Слайд 10
Упражнение 1
Может ли быть трехгранный угол с плоскими
углами: а) 30°, 60°, 20°; б) 45°, 45°, 90°;
в) 30°, 45°, 60°?Ответ: а) Нет;
б) нет;
в) да.
Слайд 11
Упражнение 2
Приведите примеры многогранников, у которых грани, пересекаясь
в вершинах, образуют только: а) трехгранные углы; б) четырехгранные
углы; в) пятигранные углы.Ответ: а) Тетраэдр, куб, додекаэдр;
б) октаэдр;
в) икосаэдр.
Слайд 12
Упражнение 3
Два плоских угла трехгранного угла равны 70°
и 80°. В каких границах находится третий плоский угол?
Ответ:
10о < ϕ < 150о.
Слайд 13
Упражнение 4
Плоские углы трехгранного угла равны 45°, 45°
и 60°. Найдите величину угла между плоскостями плоских углов
в 45°.Ответ: 90о.
Слайд 14
Упражнение 5
В трехгранном угле два плоских угла равны
по 45°; двугранный угол между ними прямой. Найдите третий
плоский угол.Ответ: 60о.
Слайд 15
Упражнение 6
Плоские углы трехгранного угла равны 60°, 60°
и 90°. На его ребрах от вершины отложены равные
отрезки OA, OB, OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC.Ответ: 90о.