под прямым углом.
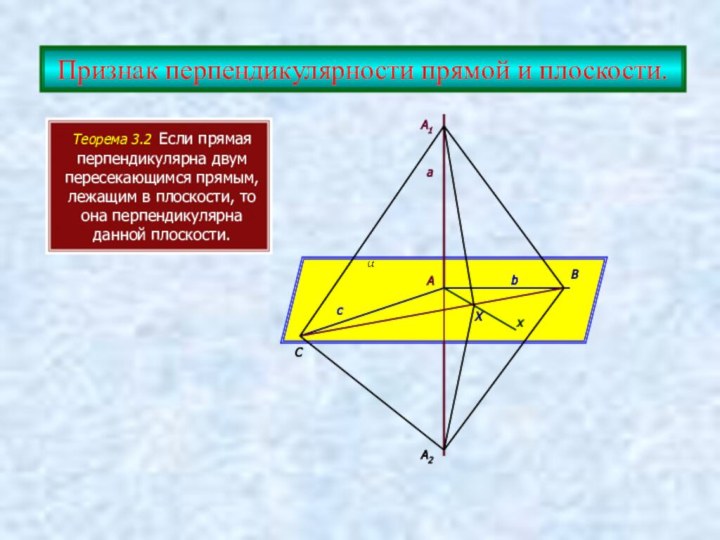
Теорема 3.1 Если две пересекающие
прямые параллельны
соответственно двум перпендикулярным прямым,
то они тоже перпендикулярны.
a
b
a1
b1
C
C1
A
A1
B
B1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



a
b
a1
b1
C
C1
A
A1
B
B1
А
В
С
D
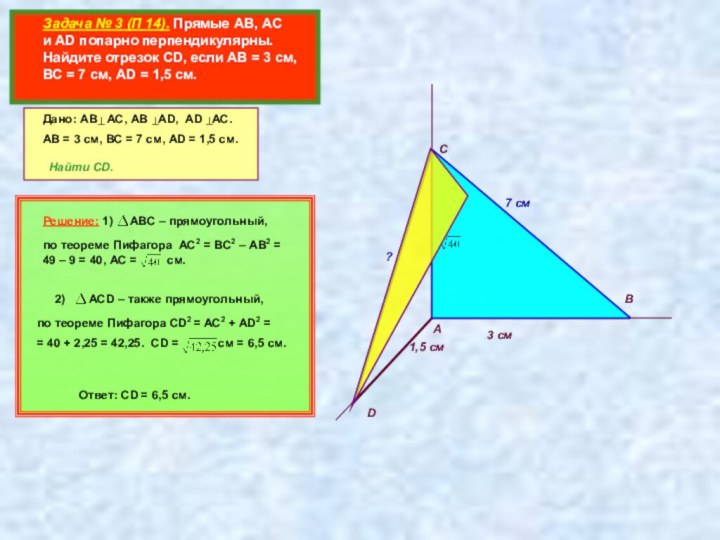
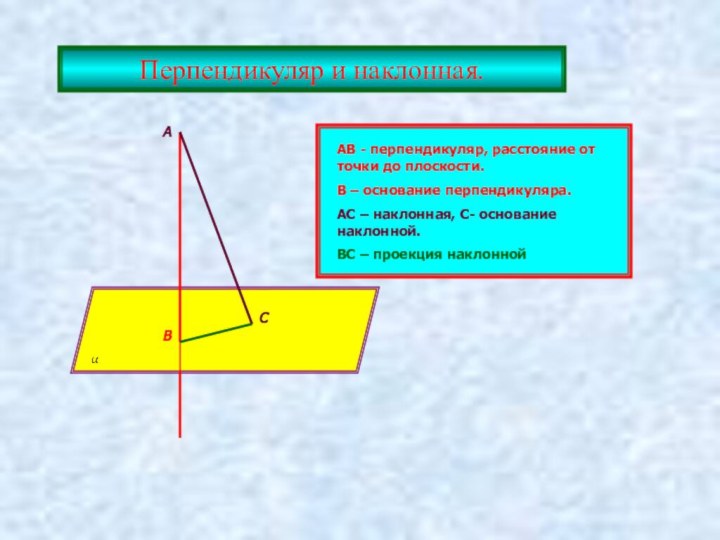
Дано: АВ АС, АВ АD, AD AC.
АВ = 3 см, ВС = 7 см, АD = 1,5 см.
3 см
7 см
1,5 см
Найти CD.
?
Решение: 1) АВС – прямоугольный,
по теореме Пифагора АС2 = ВС2 – АВ2 = 49 – 9 = 40, АС = см.
2) АСD – также прямоугольный,
по теореме Пифагора СD2 = AC2 + AD2 =
= 40 + 2,25 = 42,25. CD = cм = 6,5 см.
Ответ: CD = 6,5 см.
a
b
c
x
C
X
B
A
A1
A2
a1
a2
A1
A2
x2
x1
А
В
С
А1
с
с
a
b