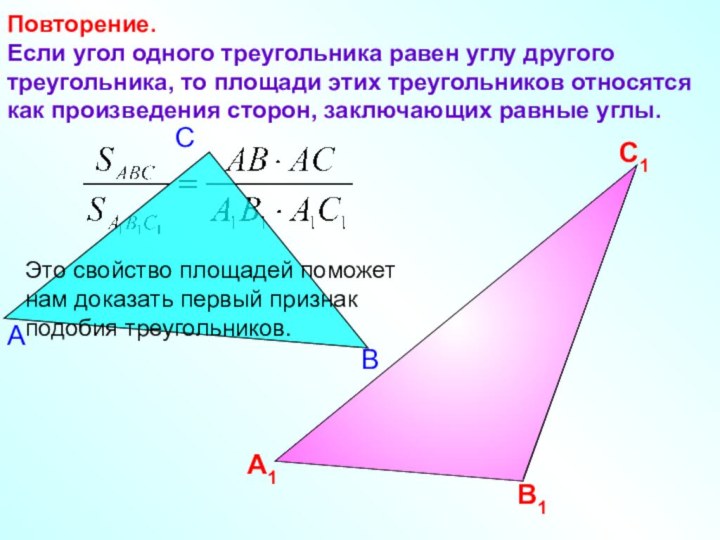
другого треугольника, то площади этих треугольников относятся как произведения
сторон, заключающих равные углы.А1
В1
С1
Это свойство площадей поможет нам доказать первый признак подобия треугольников.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



А1
В1
С1
Это свойство площадей поможет нам доказать первый признак подобия треугольников.
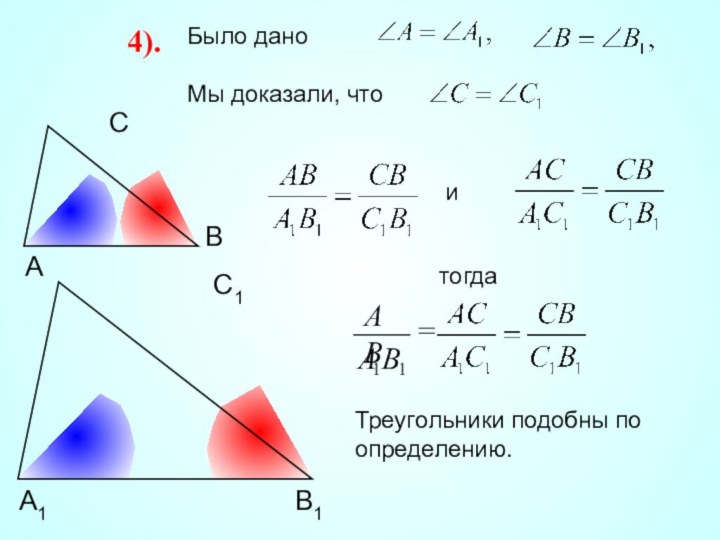
Доказательство:
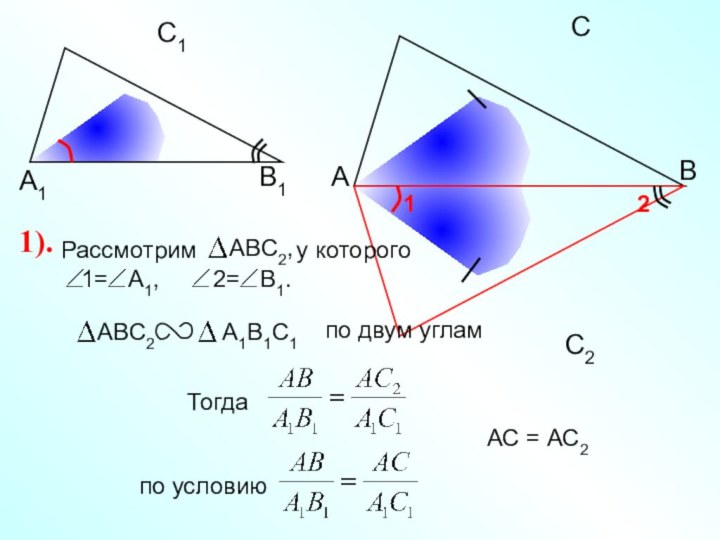
1).
А
С
В
В1
С1
А1
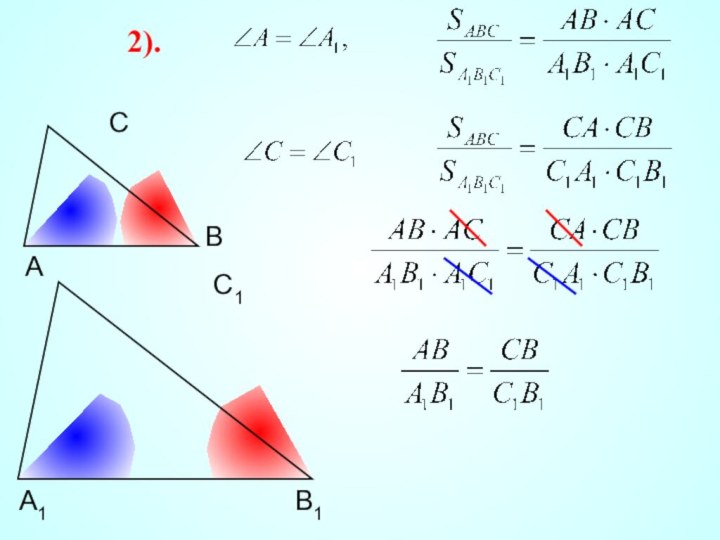
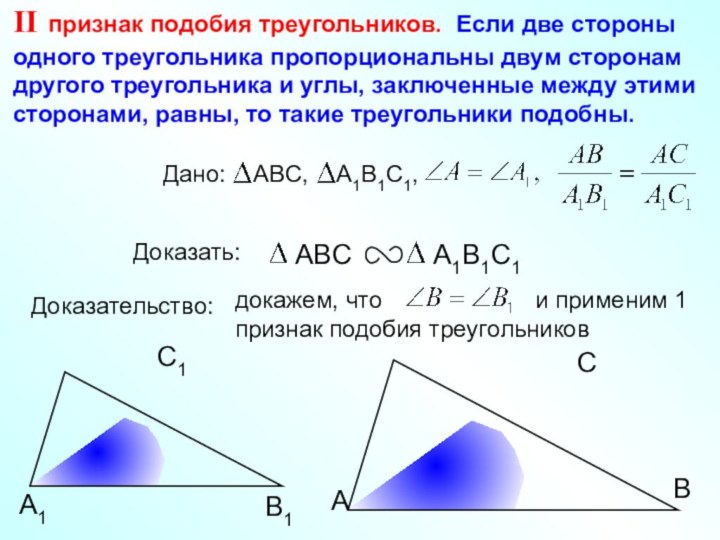
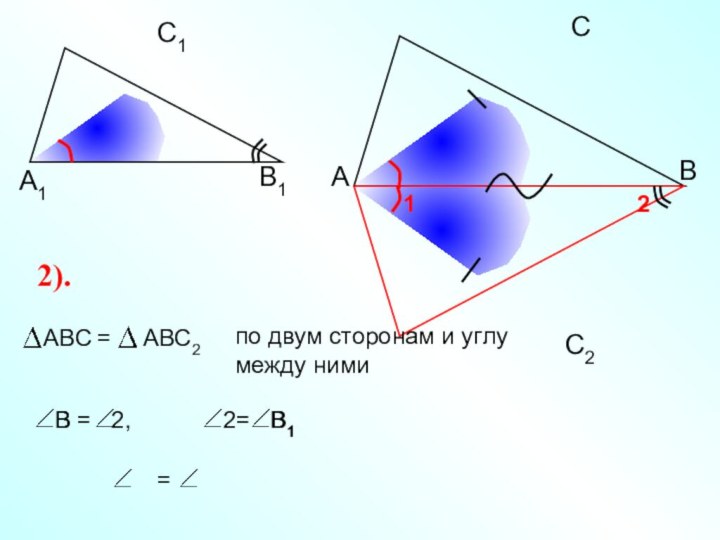
II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство:
А
С
В
В1
С1
А1
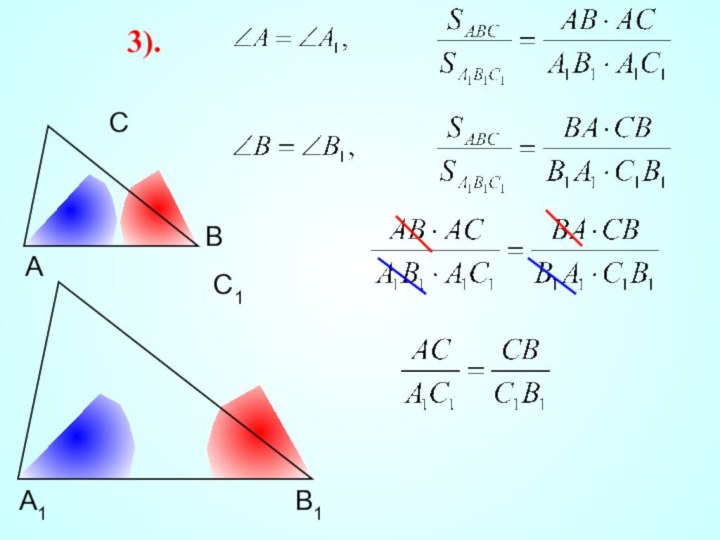
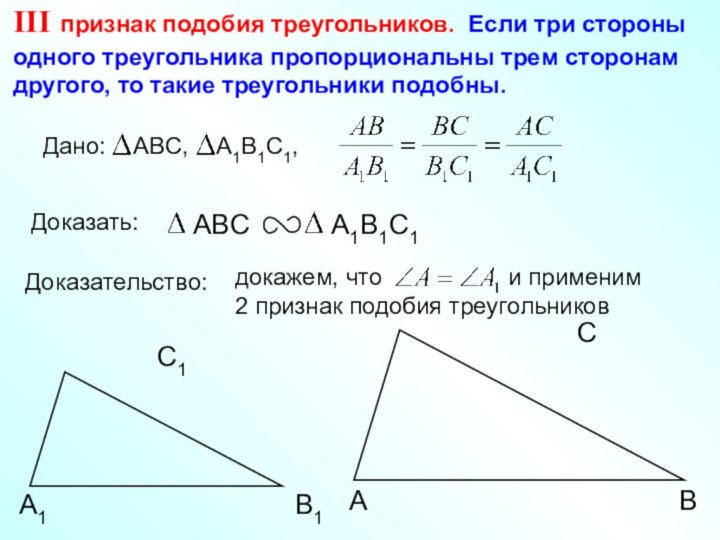
III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
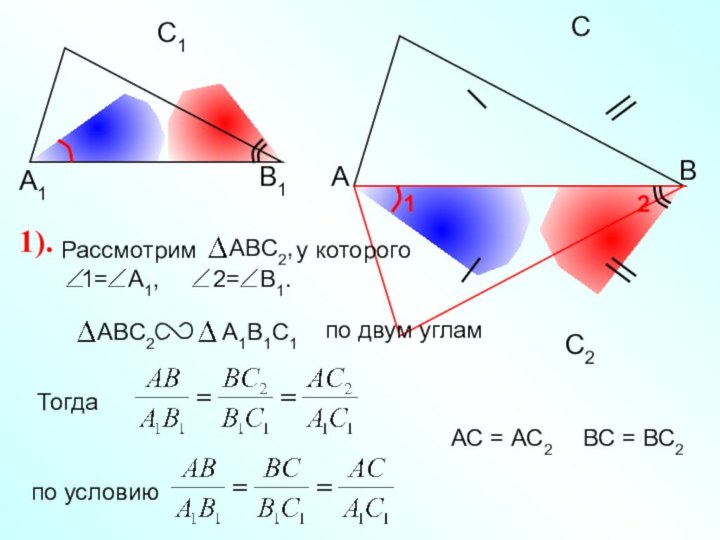
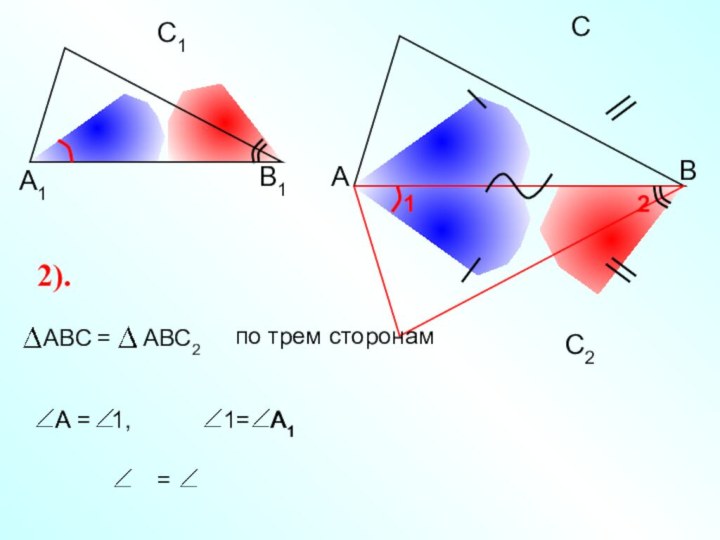
Доказательство: