- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии 10 класс
Содержание
- 2. Основные задачи урока:Ввести понятие двугранного угла и его линейного углаРассмотреть задачи на применение этих понятий
- 3. Определение: Двугранным
- 4. В обыденной жизни, форму двугранного угла имеют
- 5. Назовите предметы, имеющие форму двугранного угла
- 6. Примеры двугранных углов:
- 7. Обозначение двугранного угла.АВСDУгол CBDA
- 8. Величиной двугранного угла называется величина его линейного
- 9. Измерение двугранных углов. Линейный угол.АВМDРСАВМС =РУгол Р – линейный угол двугранного угла АВМС
- 10. Определение: Углом между двумя
- 11. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 12. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.ABOA1O1B1
- 13. Докажем, что все линейные углы двугранного угла
- 14. Способ нахождения (построения) линейного угла.1. Найти (
- 15. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.ββ1а1
- 16. Задача 1: В кубе A…D1 найдите угол между плоскостями ABC и CDD1.Ответ: 90o.
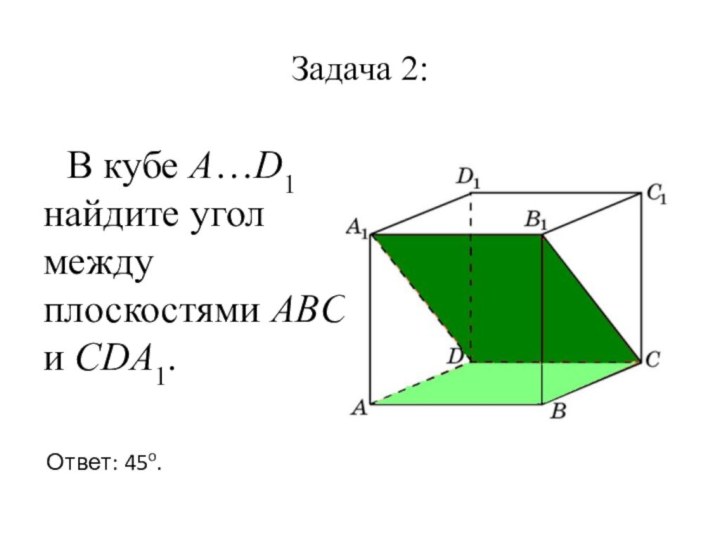
- 17. Задача 2: В кубе A…D1 найдите угол между плоскостями ABC и CDA1.Ответ: 45o.
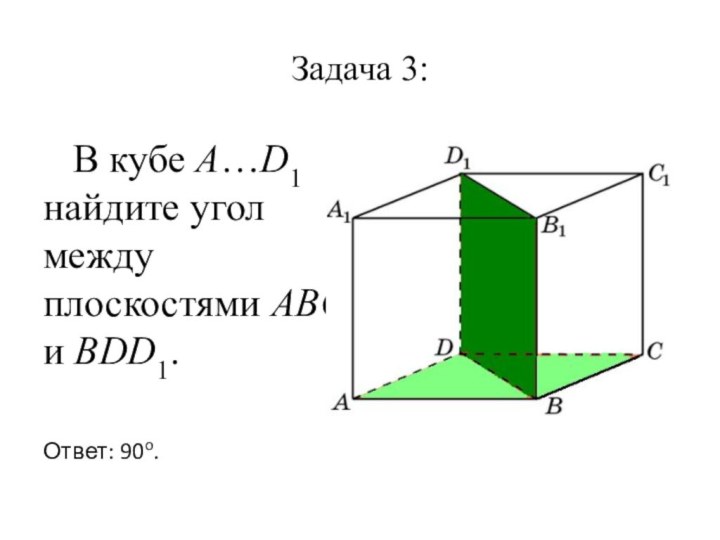
- 18. Задача 3: В кубе A…D1 найдите угол между плоскостями ABC и BDD1.Ответ: 90o.
- 19. Задача 4: В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.Ответ: 90o.
- 20. Задача 5:В кубе A…D1 найдите угол между
- 21. Задача 6:
- 22. Решение:Треугольники ABC и ADC правильные, поэтому,
- 23. Задача 7: Из вершины В
- 24. Решение:АВС – тупоугольный треугольник с тупым углом
- 25. 2) Так как АС⊥ВК, то АС⊥КВ1 (по
- 26. АС АСРи АСВпрямая СВ перпендикулярна ребру
- 27. АСАСРи АСВВ грани АСВпрямая ВО перпендикулярна
- 28. Задача №3КМРТА) Двугранный угол РТМК: (1)
- 29. Задача №3КМРТВАСАВ параллельна РТ (по построению), а
- 30. PKTMЗадача №3б) Двугранный угол РМКТ: (1) ребро
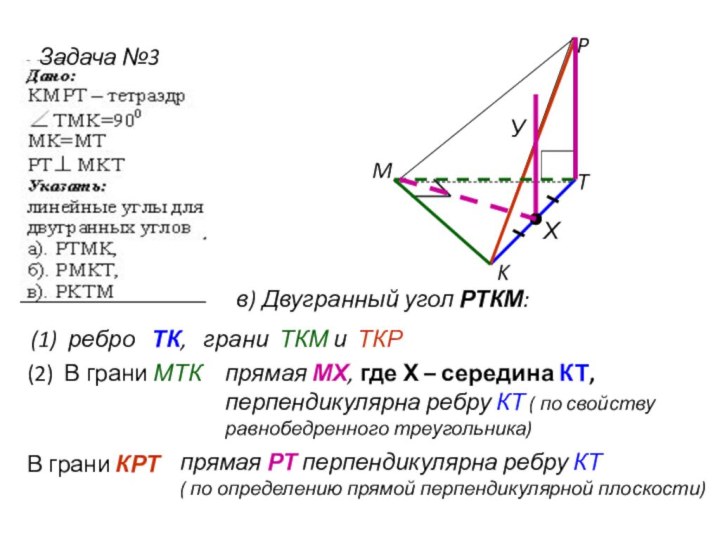
- 31. Задача №3TKPMв) Двугранный угол РТКМ: (1) ребро
- 32. Задача №3MPKTХУв) Двугранный угол РТКМ:3) Построим прямую
- 33. 1. В кубе A…D1 найдите угол между плоскостямиABC и CDD1.Ответ:
- 34. 2.В кубе A…D1 найдите угол между плоскостямиABC и CDA1.Ответ:
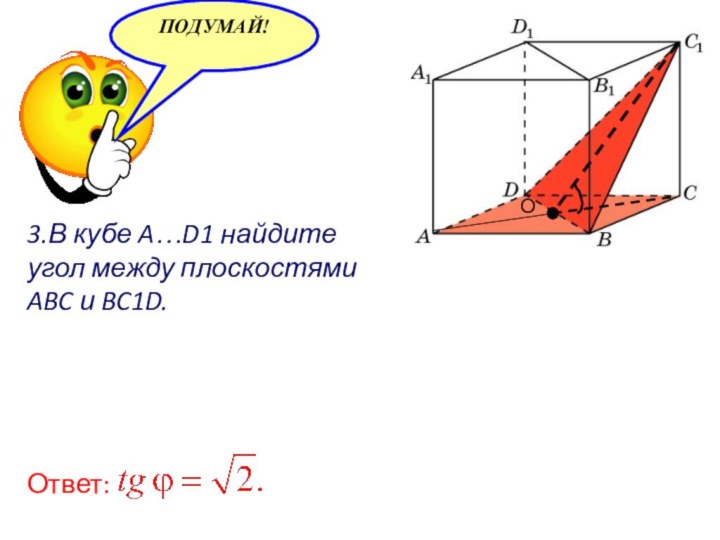
- 35. 3.В кубе A…D1 найдите угол между плоскостямиABC и BC1D.Ответ:О
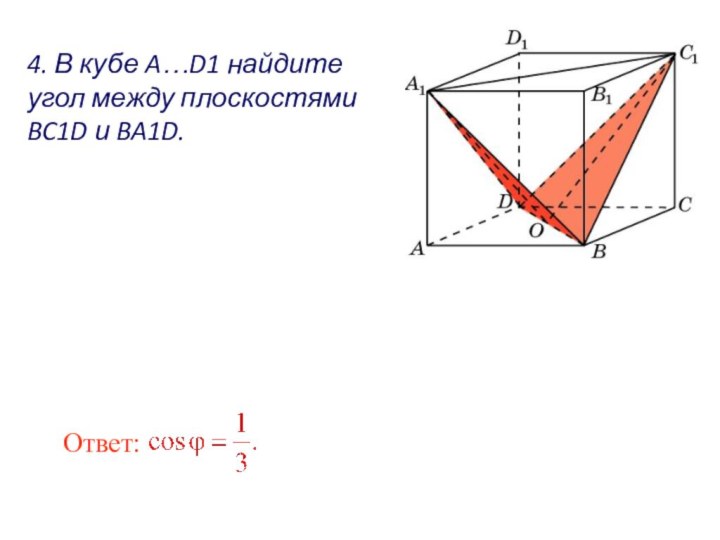
- 36. Ответ: 4. В кубе A…D1 найдите угол между плоскостямиBC1D и BA1D.
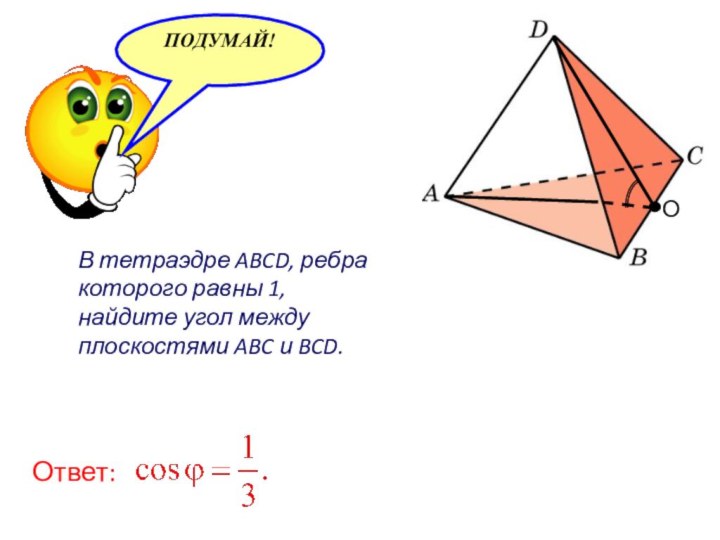
- 37. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD.ООтвет:
- 38. В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SBC и ABC.
- 39. В параллелограмме АВСD угол АDС равен
- 40. Скачать презентацию
- 41. Похожие презентации

































Слайд 3
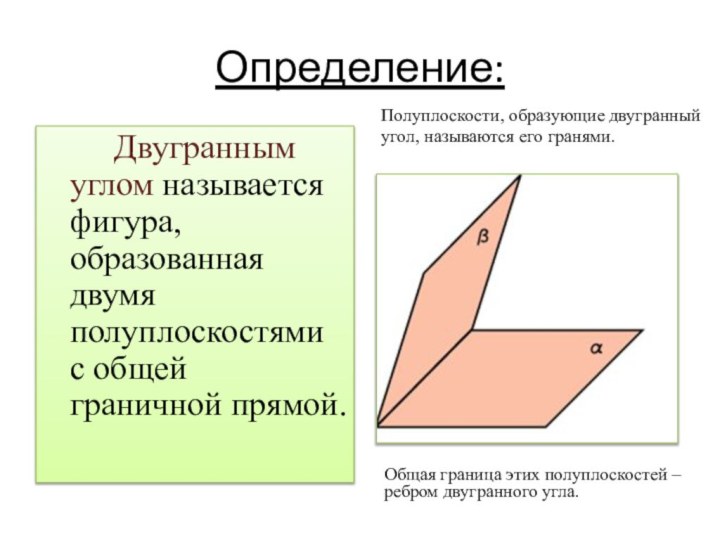
Определение:
Двугранным углом
называется фигура, образованная двумя полуплоскостями с общей граничной прямой.
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.
Слайд 8
Величиной двугранного угла называется величина его линейного угла.
AF ⊥ CD
BF ⊥ CDAFB-линейный угол двугранного угла ACDВ
Слайд 9
Измерение двугранных углов. Линейный угол.
А
В
М
D
Р
С
АВМС =
Р
Угол Р –
линейный угол двугранного угла АВМС
Слайд 10
Определение:
Углом между двумя пересекающимися
плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
Слайд 11 Линейным углом двугранного угла называется сечение двугранного угла
плоскостью, перпендикулярной ребру.
Слайд 12 Величина линейного угла не зависит от выбора его
вершины на ребре двугранного угла.
A
B
O
A1
O1
B1
Слайд 13 Докажем, что все линейные углы двугранного угла равны
друг другу.
Рассмотрим два
линейных угла АОВ и А1ОВ1. Лучи ОА и ОА1 лежат в одной грани и перпендикулярны ОО1, поэтому они сонаправлены. Лучи ОВ и ОВ1 также сонаправлены. Следовательно, ∠АОВ=∠А1ОВ1 (как углы с сонаправленными сторонами).
Слайд 14
Способ нахождения (построения) линейного угла.
1. Найти ( увидеть)
ребро и грани двугранного угла
2. В гранях найти направления
( прямые) перпендикулярные ребру3. (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
При изображении сохраняется параллельность и отношение длин параллельных отрезков
Слайд 15 Аналогично тому , как и на плоскости ,
в пространстве определяются смежные и вертикальные двугранные углы.
β
β1
а
1
Слайд 20
Задача 5:
В кубе A…D1 найдите угол между плоскостями
BC1D
и BA1D.
Решение:
Пусть О – середина ВD. A1OC1 – линейный
угол двугранного угла А1ВDС1.
Слайд 21
Задача 6:
В тетраэдре
DABC все ребра равны, точка М – середина ребра
АС. Докажите, что ∠DMB – линейный угол двугранного угла BACD.
Слайд 22
Решение:
Треугольники ABC и ADC правильные, поэтому, BM⊥AC
и DM⊥AC и, следовательно, ∠DMB является линейным углом двугранного
угла DACB.
Слайд 23
Задача 7:
Из вершины В треугольника
АВС, сторона АС которого лежит в плоскости α, проведен
к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ1 равен 450.
Слайд 24
Решение:
АВС – тупоугольный треугольник с тупым углом А,
поэтому основание высоты ВК лежит на продолжении стороны АС.
ВК – расстояние от точки В до АС.
ВВ1 – расстояние от точки В до плоскости α
Слайд 25 2) Так как АС⊥ВК, то АС⊥КВ1 (по теореме
, обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ1 –
линейный угол двугранного угла ВАСВ1 и ∠ВКВ1=450.3) ∆ВАК:
∠А=300, ВК=ВА·sin300, ВК =1.
∆ВКВ1:
ВВ1=ВК·sin450, ВВ1=
Слайд 26
АС
АСР
и АСВ
прямая СВ перпендикулярна ребру СА
( по условию)
В грани АСВ
В грани АСР
прямая СР перпендикулярна
ребру СА ( по теореме о трех перпендикулярах)
угол РСВ - линейный для двугранного угла с ребром АС
Слайд 27
АС
АСР
и АСВ
В грани АСВ
прямая ВО перпендикулярна ребру
СА
( по свойству равностороннего треугольника)
В грани АСР
прямая РК
перпендикулярна ребру СА ( по теореме о трех перпендикулярах)
Угол РКВ - линейный для двугранного угла с РСАВ
К
Слайд 28
Задача №3
К
М
Р
Т
А) Двугранный угол РТМК:
(1) ребро
МТ, грани МТР и МТК
(2) В грани
МТРпрямая ТР перпендикулярна ребру МТ
( по определению прямой, перпендикулярной плоскости)
В грани МТК
прямая МК перпендикулярна ребру МТ
( по условию)
В
А
С
Слайд 29
Задача №3
К
М
Р
Т
В
А
С
АВ параллельна РТ (по построению), а так
как РТ перпендикулярна ребру МТ ( по доказанному), то
АВ перпендикулярна ребру МТ (по лемме о связи параллельности и перпендикулярности) Аналогично ВС перпендикулярна ребру МТ. Значит, угол АВС – искомый
Слайд 30
P
K
T
M
Задача №3
б) Двугранный угол РМКТ:
(1) ребро
МК, грани МКР и МКТ
(2) В грани МТК
прямая
МТ перпендикулярна ребру МК ( по условию)В грани МКР
прямая МР перпендикулярна ребру МК
( по теореме о трех перпендикулярах)
Ответ. Угол РМТ - линейный для двугранного угла с РМКТ
Слайд 31
Задача №3
T
K
P
M
в) Двугранный угол РТКМ:
(1) ребро
ТК, грани ТКМ и ТКР
(2) В грани МТК
прямая
МХ, где Х – середина КТ, перпендикулярна ребру КТ ( по свойству равнобедренного треугольника)Х
В грани КРТ
прямая РТ перпендикулярна ребру КТ
( по определению прямой перпендикулярной плоскости)
У
Слайд 32
Задача №3
M
P
K
T
Х
У
в) Двугранный угол РТКМ:
3) Построим прямую УХ
параллельно прямой РТ , она будет лежать в плоскости
РКТ (почему?) получим , что прямая ХУ перпендикулярно ребру КТ(по лемме о связи параллельности и перпендикулярности)
Значит, искомый угол УХМ
Слайд 38 В правильной пирамиде SABCD, все ребра которой равны
1, найдите угол между плоскостями SBC и ABC.
Слайд 39 В параллелограмме АВСD угол АDС равен
, АD = 8 см,
DС= 6
см , прямая РС перпендикулярна плоскости (АВС), РС= 9 см.Найти величину двугранного угла с ребром АD и площадь
параллелограмма.
Решение:
H
120