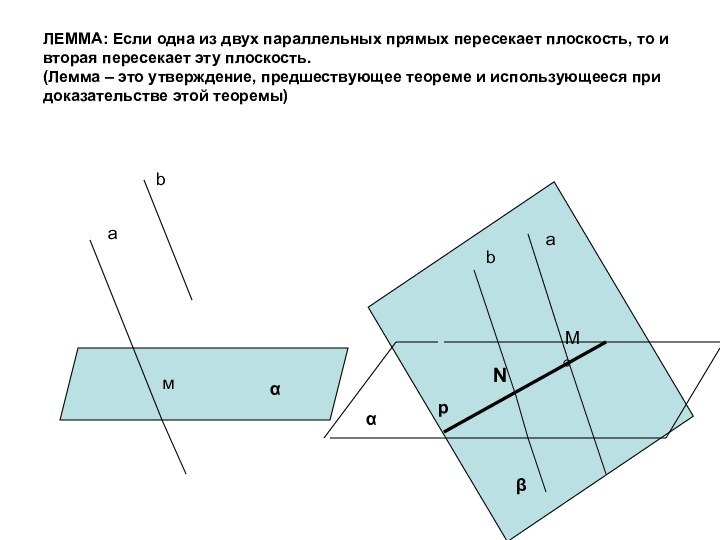
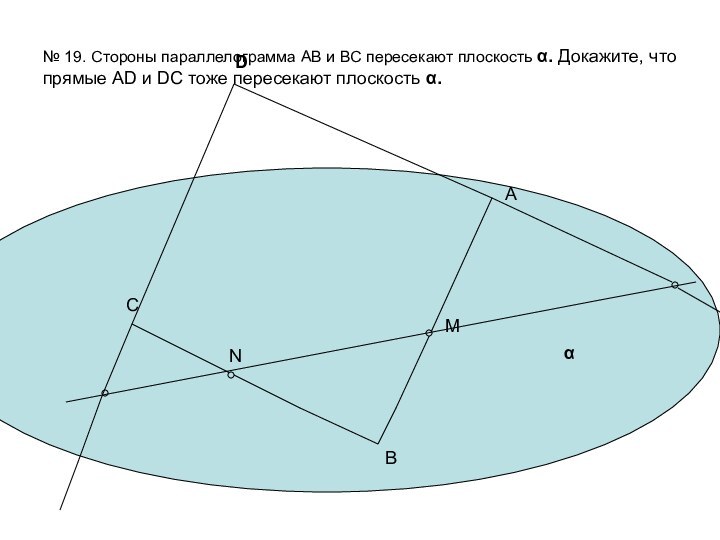
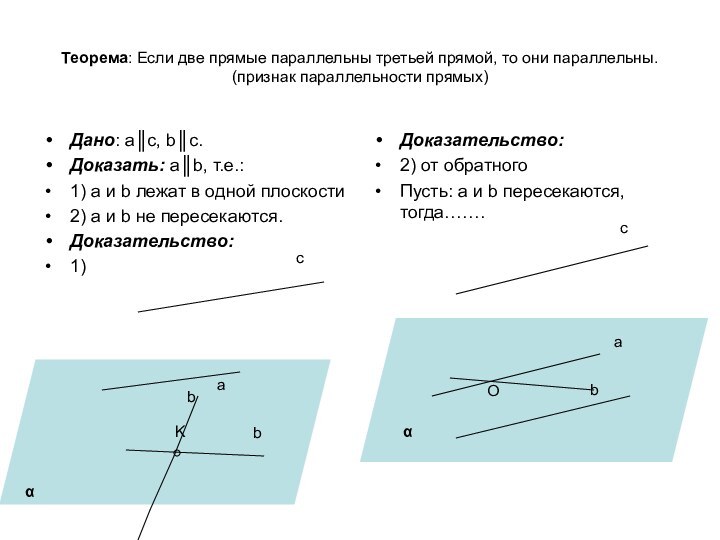
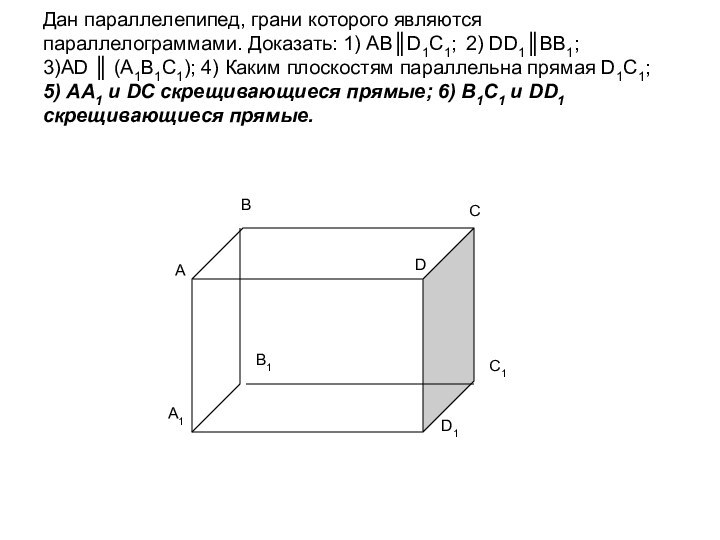
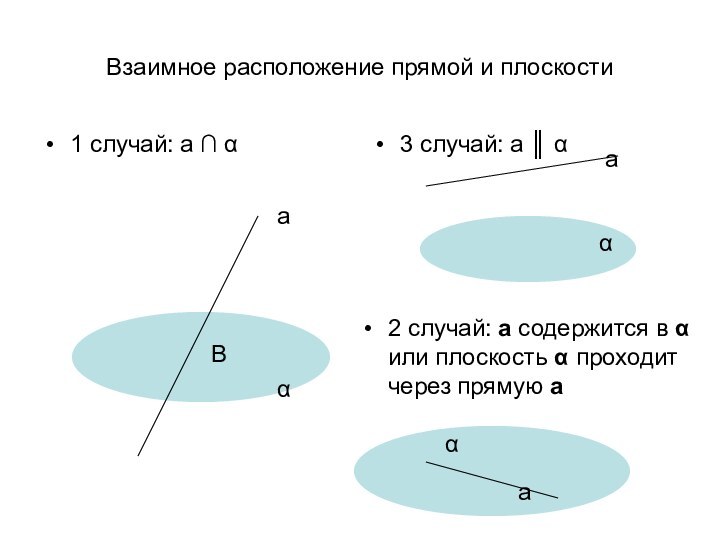
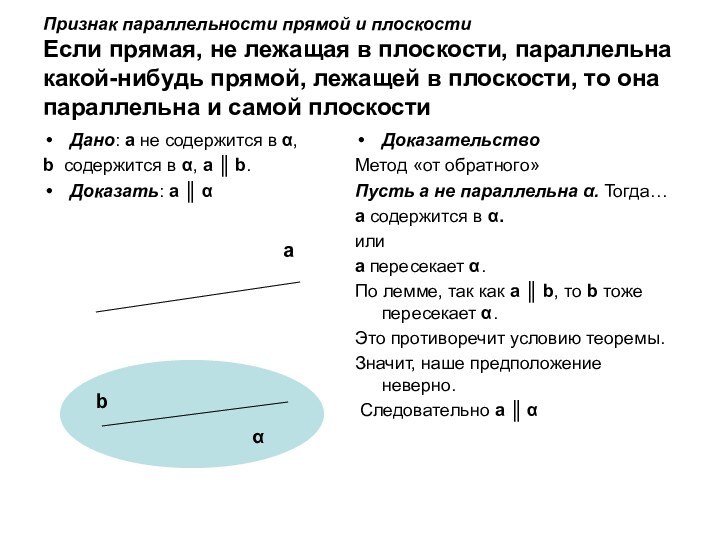
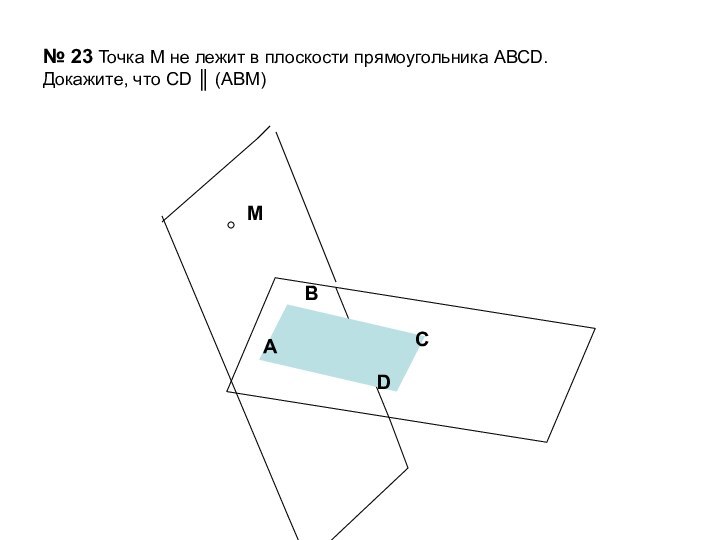
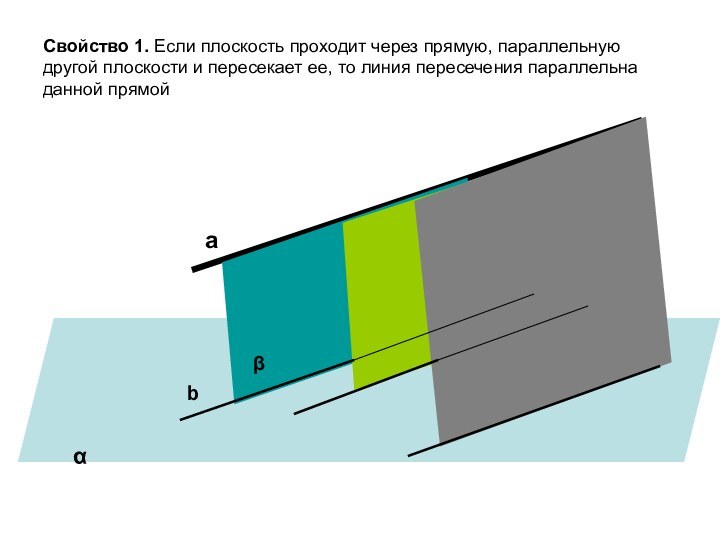
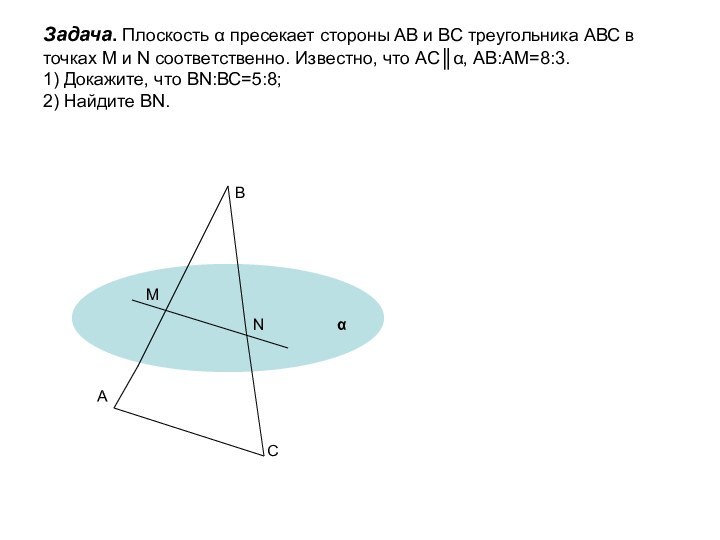
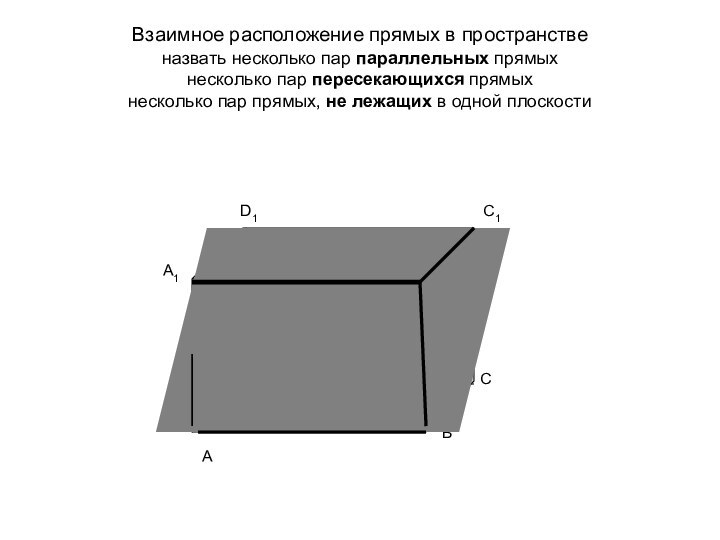
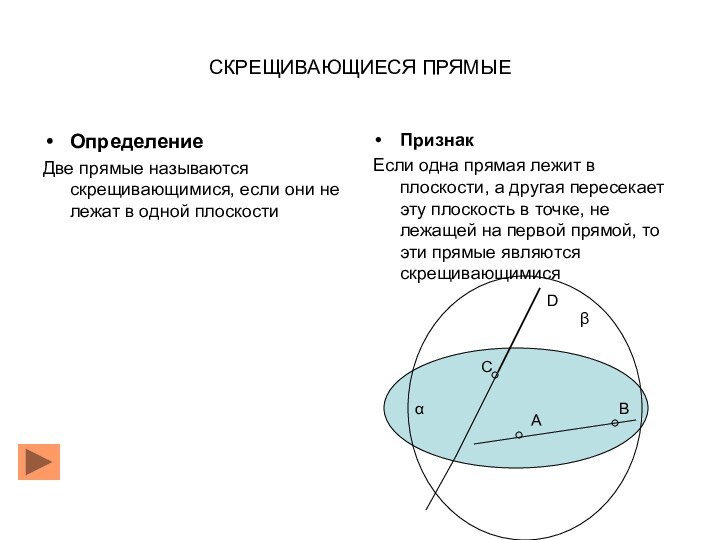
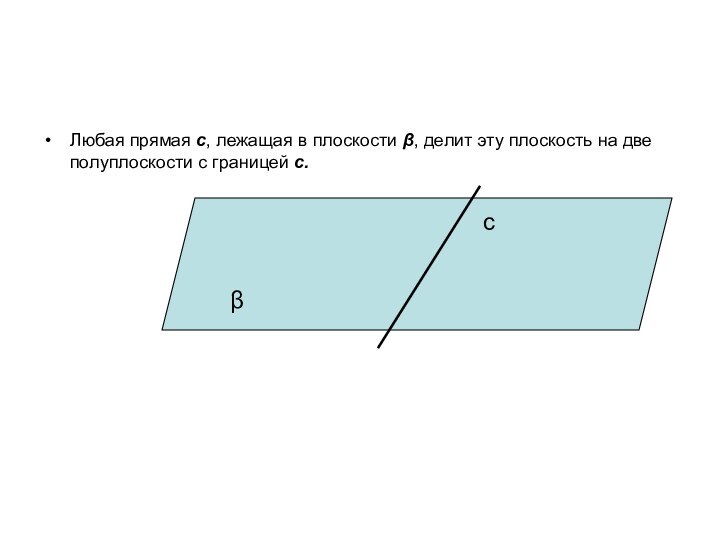
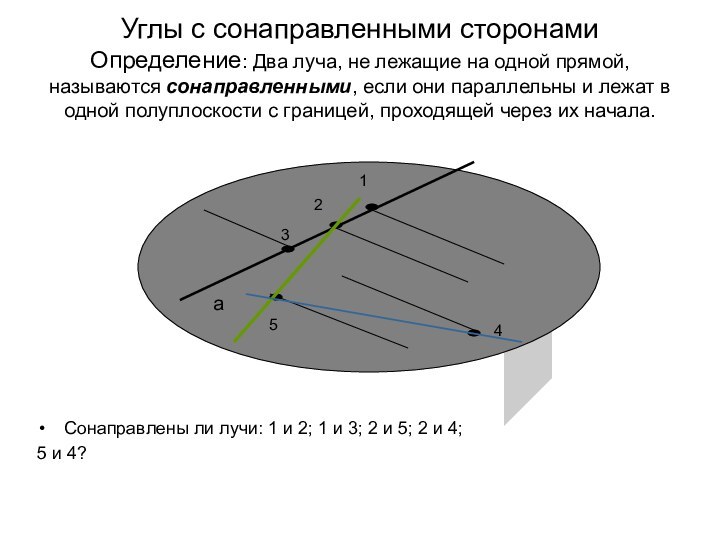
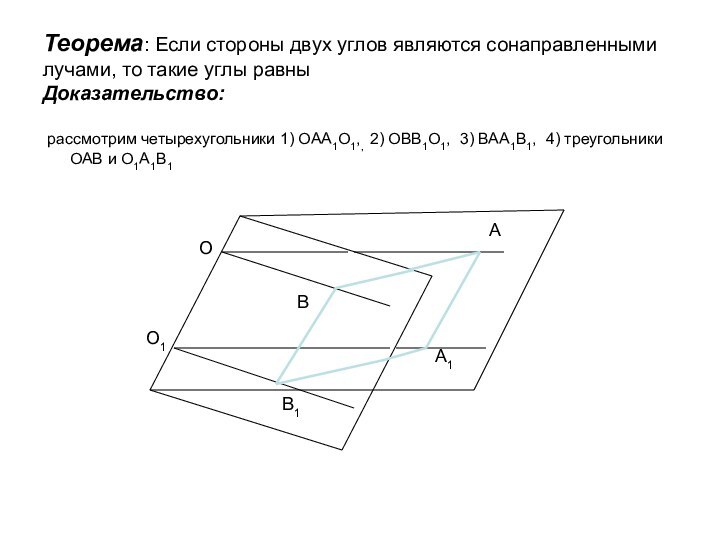
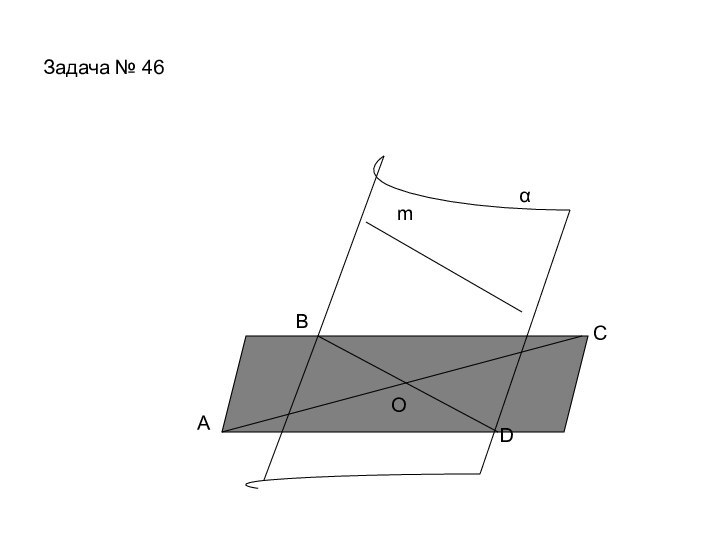
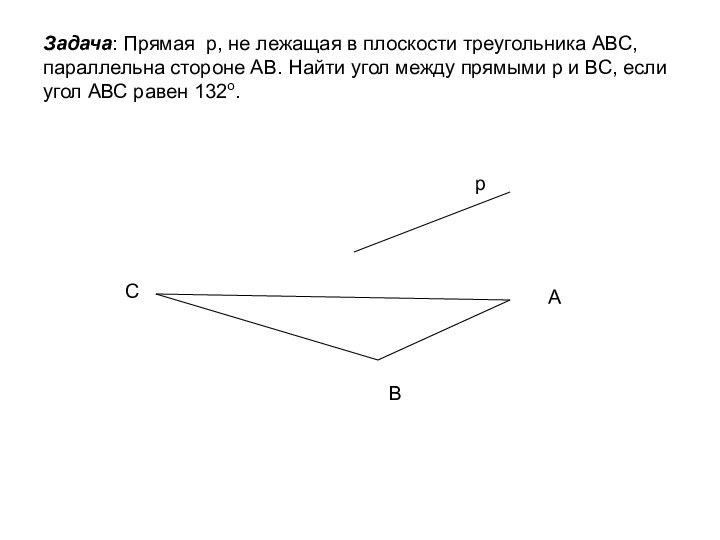
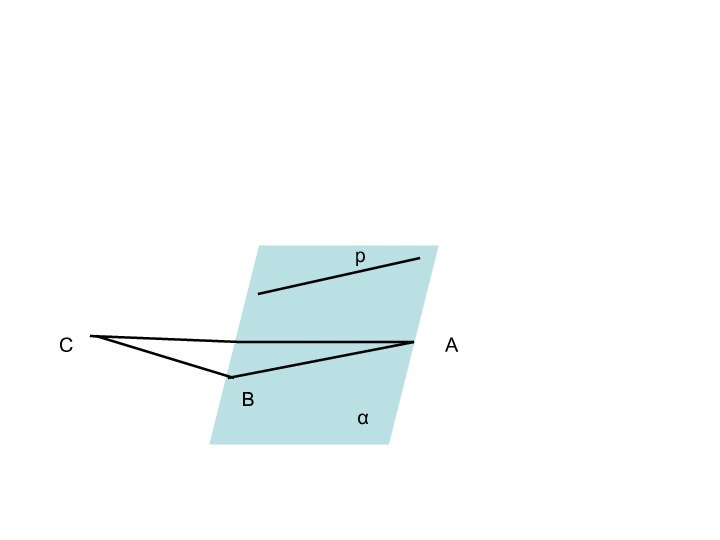
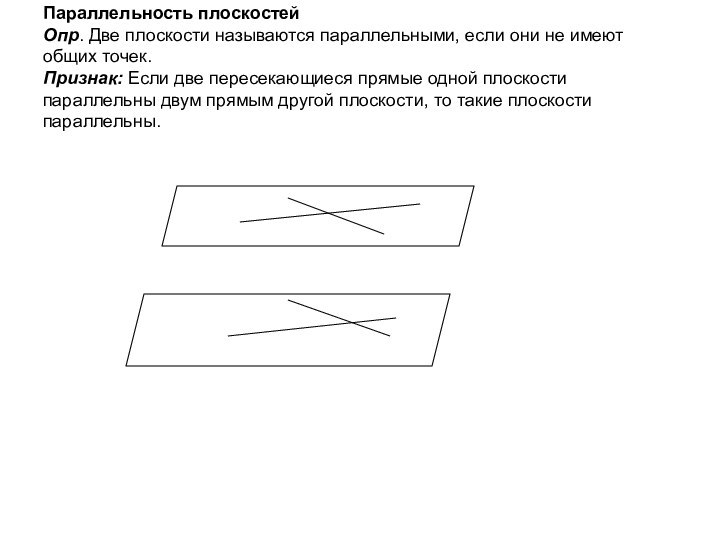
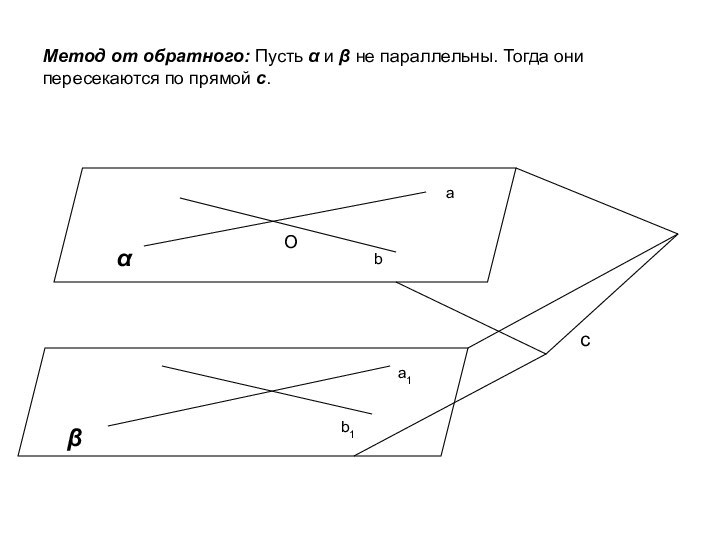
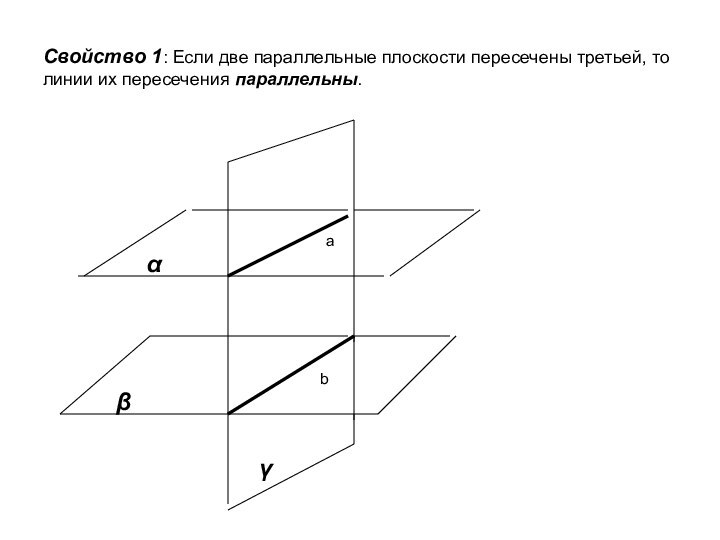
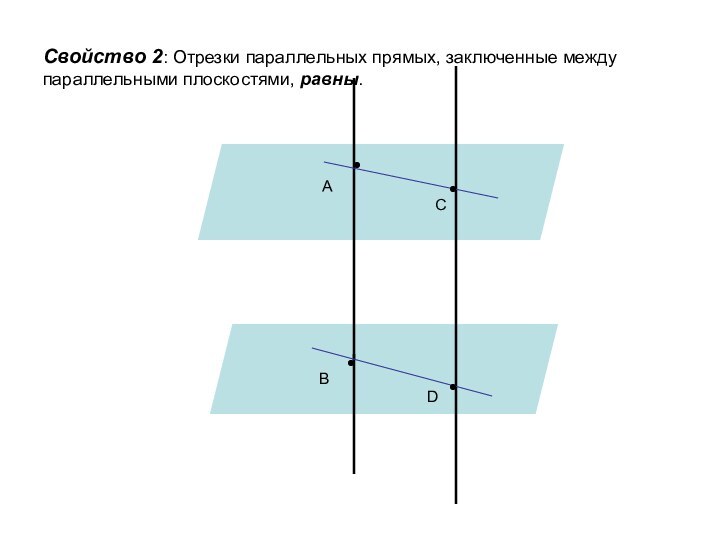
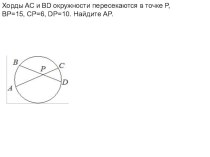
ложно?
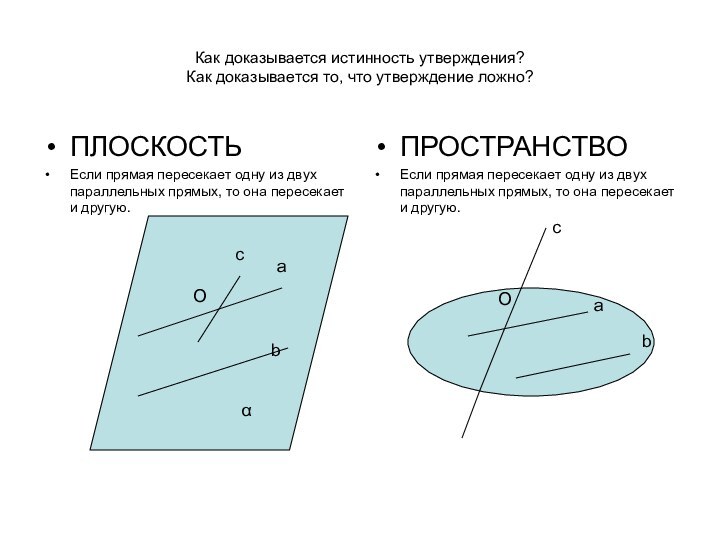
ПЛОСКОСТЬ
Если прямая пересекает одну из двух параллельных прямых, то
она пересекает и другую.ПРОСТРАНСТВО
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
α
а
b
c
О
с
а
b
О