Слайд 2
Осевая симметрия
Точки A и A' пространства называются симметричными
относительно прямой a, называемой осью симметрии, если прямая a
проходит через середину отрезка AA' и перпендикулярна этому отрезку. Точки прямой a считаются симметричными сами себе.
Фигура Ф в пространстве называется симметричной относительно оси a, если каждая точка A фигуры Ф симметрична относительно этой оси некоторой точке A' фигуры Ф.
Например, прямоугольный параллелепипед симметричен относительно оси, проходящей через центры противоположных граней, прямой круговой цилиндр симметричен относительно своей оси и т. д.
Слайд 3
Зеркальная симметрия
Точки A и A' в пространстве называются
симметричными относительно плоскости α, называемой плоскостью симметрии, если эта
плоскость проходит через середину отрезка AA' и перпендикулярна к нему. Точки плоскости α считаются симметричными сами себе. Симметрия относительно плоскости называется также зеркальной симметрией.
Фигура Ф в пространстве называется зеркально-симметричной относительно плоскости α, если каждая точка A фигуры Ф симметрична относительно этой плоскости некоторой точке A' фигуры Ф.
Например, прямоугольный параллелепипед зеркально-симметричен относительно плоскости, проходящей через ось симметрии и параллельной одной из граней. Цилиндр зеркально-симметричен относительно любой плоскости, проходящей через его ось и т. д.
Слайд 4
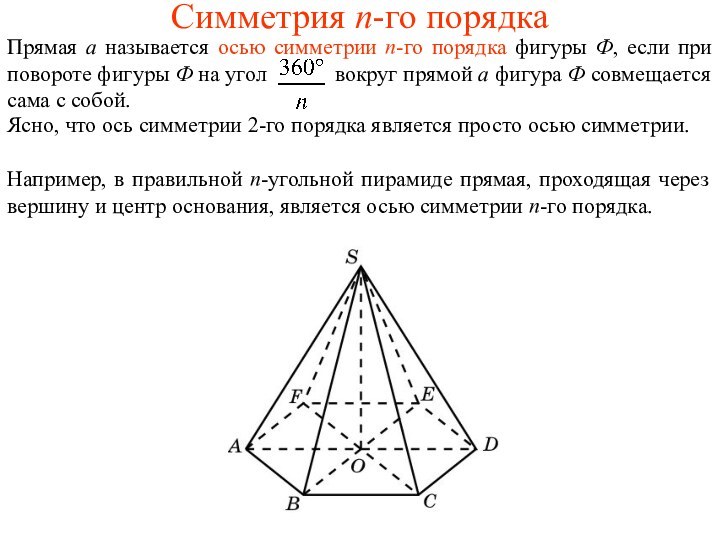
Симметрия n-го порядка
Прямая a называется осью симметрии n-го
порядка фигуры Ф, если при повороте фигуры Ф на
угол вокруг прямой a фигура Ф совмещается сама с собой.
Ясно, что ось симметрии 2-го порядка является просто осью симметрии.
Например, в правильной n-угольной пирамиде прямая, проходящая через вершину и центр основания, является осью симметрии n-го порядка.
Слайд 5
Упражнение 1
Приведите примеры центрально-симметричных и не центрально-симметричных фигур.
Ответ:
Центрально-симметричные: куб, прямоугольный параллелепипед, шар и др.; не центрально-симметричные:
пирамида, конус и др.
Слайд 6
Упражнение 2
Может ли центр симметрии фигуры не принадлежать
ей?
Ответ: Да.
Слайд 7
Упражнение 3
Может ли фигура иметь более одного центра
симметрии?
Ответ: Да, например, прямая, плоскость и т.д. имеют бесконечно
много центров симметрии.
Слайд 8
Упражнение 4
Может ли фигура иметь ровно два центра
симметрии?
Слайд 9
Упражнение 5
Имеет ли центр симметрии: а) правильный тетраэдр;
б) куб; в) октаэдр; г) икосаэдр; д) додекаэдр?
Ответ: а)
Нет;
б) да;
в) да;
г) да;
д) да.
Слайд 10
Упражнение 6
Имеет ли центр симметрии правильная пятиугольная призма?
Ответ:
Нет.
Слайд 11
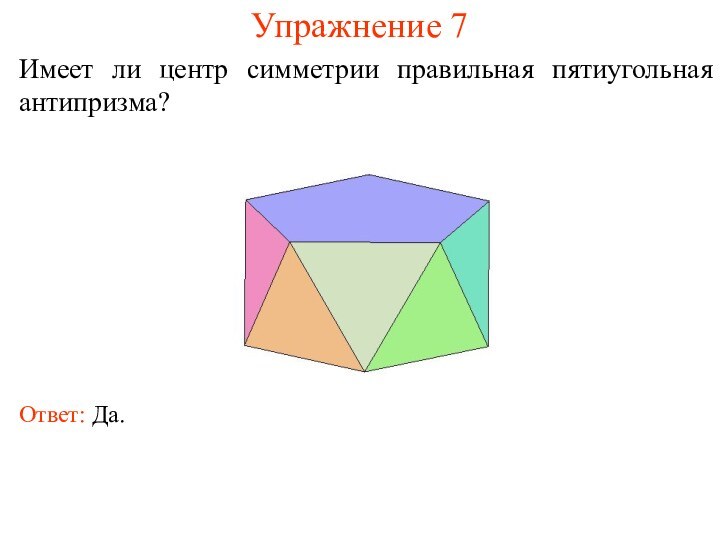
Упражнение 7
Имеет ли центр симметрии правильная пятиугольная антипризма?
Ответ:
Да.
Слайд 12
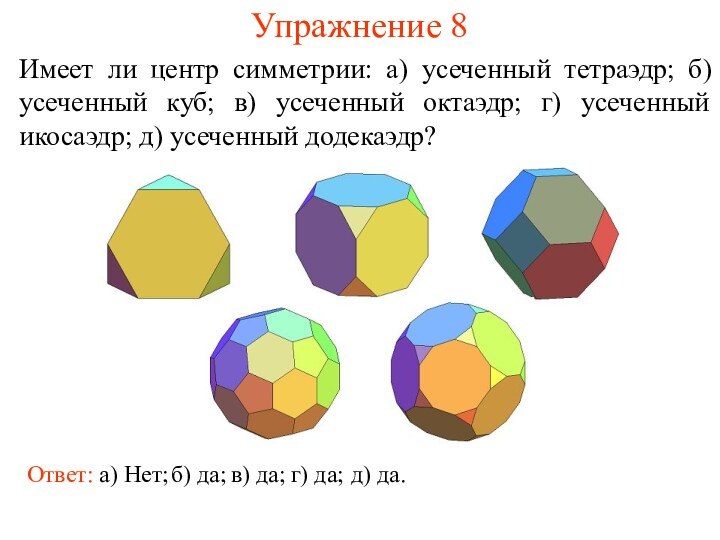
Упражнение 8
Имеет ли центр симметрии: а) усеченный тетраэдр;
б) усеченный куб; в) усеченный октаэдр; г) усеченный икосаэдр;
д) усеченный додекаэдр?
Ответ: а) Нет;
б) да;
в) да;
г) да;
д) да.
Слайд 13
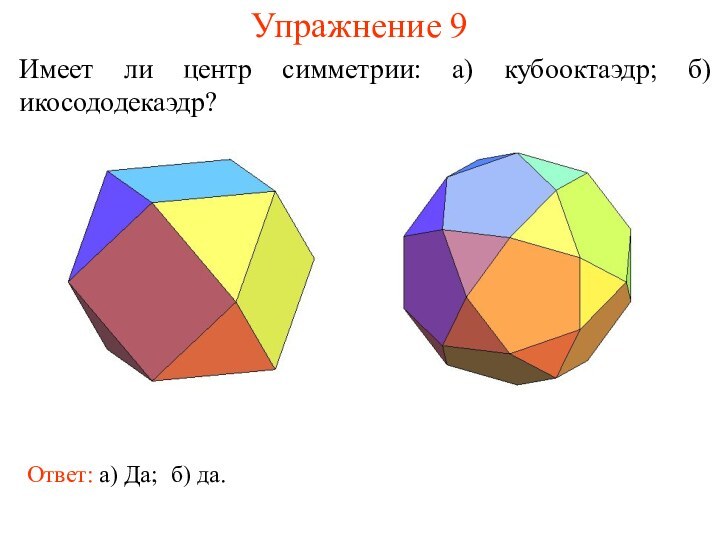
Упражнение 9
Имеет ли центр симметрии: а) кубооктаэдр; б)
икосододекаэдр?
Ответ: а) Да;
б) да.
Слайд 14
Упражнение 10
Имеет ли центр симметрии: а) усеченный кубооктаэдр;
б) усеченный икосододекаэдр?
Ответ: а) Да;
б) да.
Слайд 15
Упражнение 11
Имеет ли центр симметрии: а) ромбокубооктаэдр; б)
ромбоикосододекаэдр?
Ответ: а) Да;
б) да.
Слайд 16
Упражнение 12
Имеет ли центр симметрии: а) курносый куб;
б) курносый додекаэдр?
Ответ: а) Нет;
б) нет.
Слайд 17
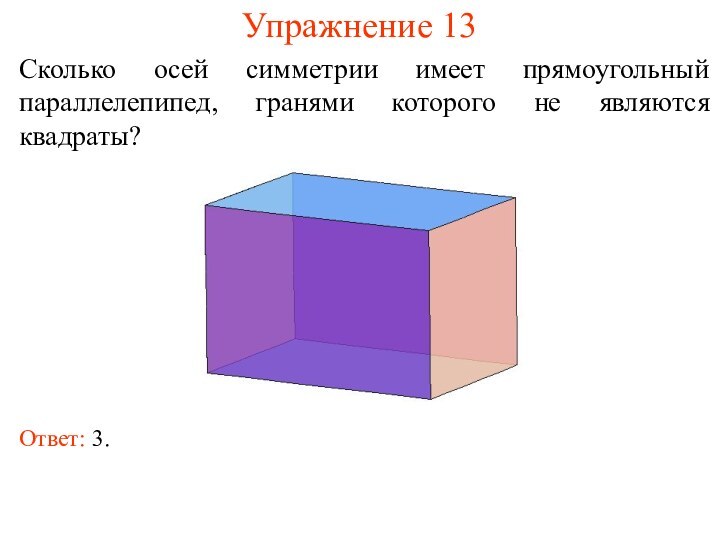
Упражнение 13
Сколько осей симметрии имеет прямоугольный параллелепипед, гранями
которого не являются квадраты?
Ответ: 3.
Слайд 18
Упражнение 14
Сколько осей симметрии имеет прямоугольный параллелепипед, две
грани которого являются квадратами?
Ответ: 5.
Слайд 19
Упражнение 15
Сколько осей симметрии имеет шар?
Ответ: Бесконечно много.
Слайд 20
Упражнение 16
Приведите примеры пространственных фигур с осями симметрии
3-го, 4-го и т. д. порядков.
Ответ: Правильные 3-угольные, 4-угольные
пирамиды.
Слайд 21
Упражнение 17
Какие оси симметрии имеет правильная пятиугольная призма?
Ответ:
Пять осей симметрии второго порядка и одну ось симметрии
пятого порядка.
Слайд 22
Упражнение 18
Какие оси симметрии имеет правильная пятиугольная антипризма?
Ответ:
Нет.
Слайд 23
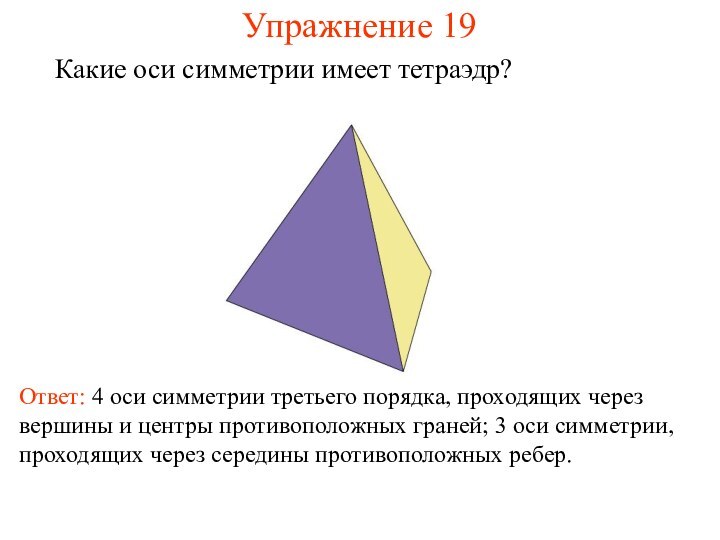
Упражнение 19
Какие оси симметрии имеет тетраэдр?
Ответ: 4 оси
симметрии третьего порядка, проходящих через вершины и центры противоположных
граней; 3 оси симметрии, проходящих через середины противоположных ребер.
Слайд 24
Упражнение 20
Какие оси симметрии имеет куб?
Ответ: 4 оси
симметрии третьего порядка, проходящих через противоположные вершины; 6 осей
симметрии, проходящих через середины противоположных ребер; 3 оси симметрии четвертого порядка, проходящих через центры противоположных граней.
Слайд 25
Упражнение 21
Какие оси симметрии имеет октаэдр?
Ответ: 3 оси
симметрии четвертого порядка, проходящих через противоположные вершины; 6 осей
симметрии, проходящих через середины противоположных ребер; 4 оси симметрии третьего порядка, проходящих через центры противоположных граней.
Слайд 26
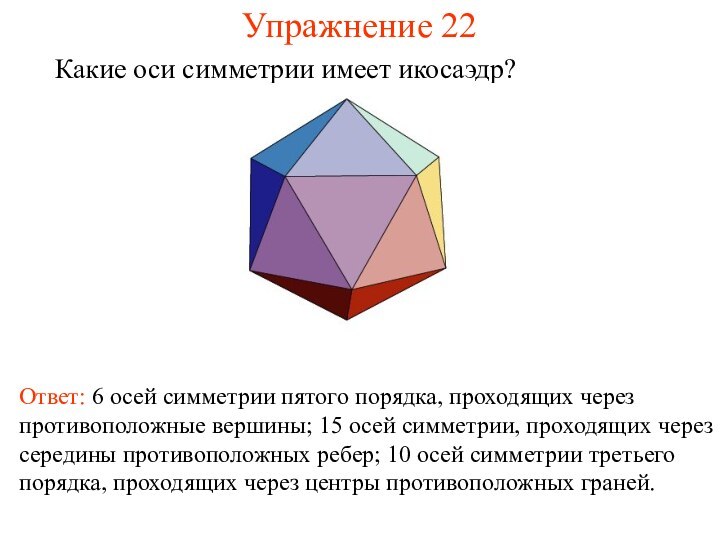
Упражнение 22
Какие оси симметрии имеет икосаэдр?
Ответ: 6 осей
симметрии пятого порядка, проходящих через противоположные вершины; 15 осей
симметрии, проходящих через середины противоположных ребер; 10 осей симметрии третьего порядка, проходящих через центры противоположных граней.
Слайд 27
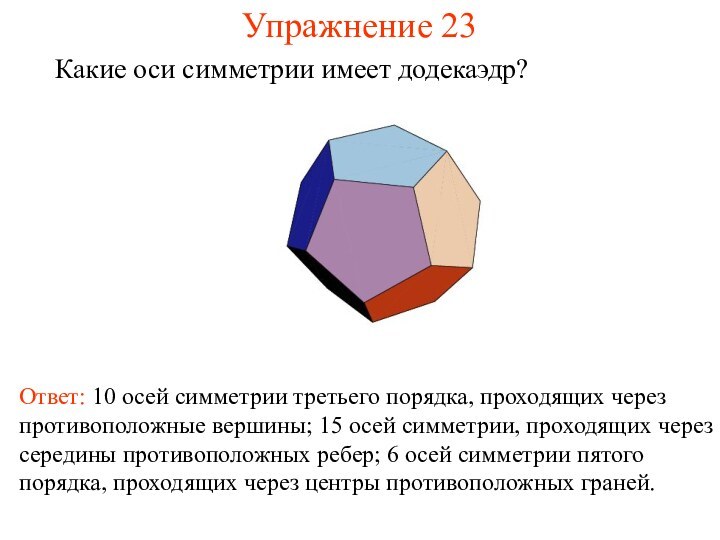
Упражнение 23
Какие оси симметрии имеет додекаэдр?
Ответ: 10 осей
симметрии третьего порядка, проходящих через противоположные вершины; 15 осей
симметрии, проходящих через середины противоположных ребер; 6 осей симметрии пятого порядка, проходящих через центры противоположных граней.
Слайд 28
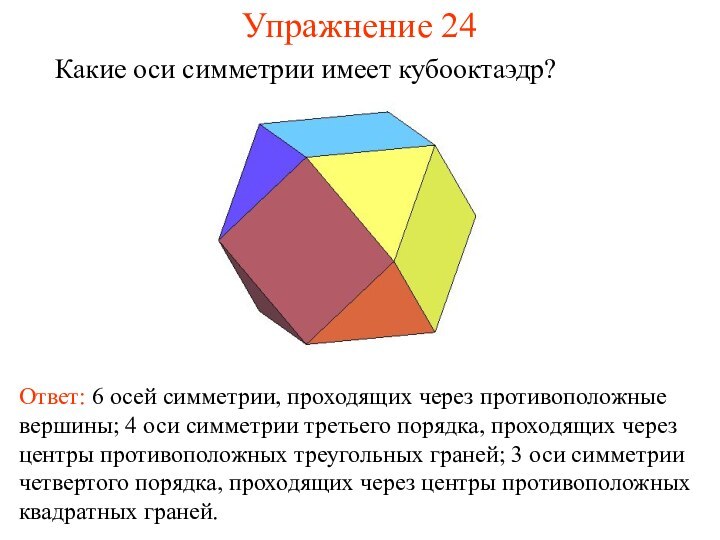
Упражнение 24
Какие оси симметрии имеет кубооктаэдр?
Ответ: 6 осей
симметрии, проходящих через противоположные вершины; 4 оси симметрии третьего
порядка, проходящих через центры противоположных треугольных граней; 3 оси симметрии четвертого порядка, проходящих через центры противоположных квадратных граней.
Слайд 29
Упражнение 25
Какие оси симметрии имеет икосододекаэдр?
Ответ: 15 осей
симметрии, проходящих через противоположные вершины; 10 осей симметрии третьего
порядка, проходящих через центры противоположных треугольных граней; 6 осей симметрии пятого порядка, проходящих через центры противоположных пятиугольных граней.
Слайд 30
Упражнение 26
Приведите пример фигуры, имеющей центр симметрии, но
не имеющей оси симметрии.
Ответ: Наклонный параллелепипед.
Слайд 31
Упражнение 27
Приведите пример фигуры, имеющей ось симметрии, но
не имеющей центра симметрии.
Ответ: Правильная четырехугольная пирамида.
Слайд 32
Упражнение 28
Укажите центр, оси и плоскости симметрии фигуры,
состоящей из двух пересекающихся прямых.
Ответ: Центр симметрии – точка
пересечения данных прямых. Оси симметрии – две прямые, содержащие биссектрисы углов, образованные данными прямыми, и прямая, проходящая через точку пересечения данных прямых и перпендикулярная их плоскости. Если данные прямые перпендикулярны, то сами они также являются осями симметрии. Плоскости симметрии: плоскость данных прямых и две плоскости, проходящие через биссектрисы углов, образованные данными прямыми и перпендикулярные их плоскости.
Слайд 33
Упражнение 29
Сколько плоскостей симметрии имеет прямоугольный параллелепипед, гранями
которого не являются квадраты?
Ответ: 3.
Слайд 34
Упражнение 30
Сколько плоскостей симметрии имеет правильная шестиугольная призма?
Ответ:
Слайд 35
Упражнение 31
Сколько плоскостей симметрии имеет: а) правильный тетраэдр;
б) куб; в) октаэдр; г) икосаэдр; д) додекаэдр?
Ответ: а)
6;
б) 9;
в) 9;
г) 15;
д) 15.
Слайд 36
Упражнение 32
Сколько плоскостей симметрии имеет кубооктаэдр?
Ответ: 9.
Слайд 37
Упражнение 33
Сколько плоскостей симметрии имеет икосододекаэдр?
Ответ: 15.