- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Сфера,шар
Содержание
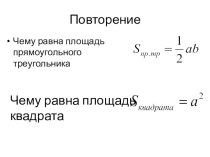
- 2. Окружность
- 4. Центром сферы является данная точка, в данном
- 5. Шаром называется тело, ограниченное сферой.Шаром радиуса R
- 6. Пусть О – центр(х0; y0; z0)MО – радиус, тогдаMО²=(x- х0)²+(y- y0)²+(z- z0)²;(x- х0)²+(y- y0)²+(z-z0)²=R²Уравнение сферы
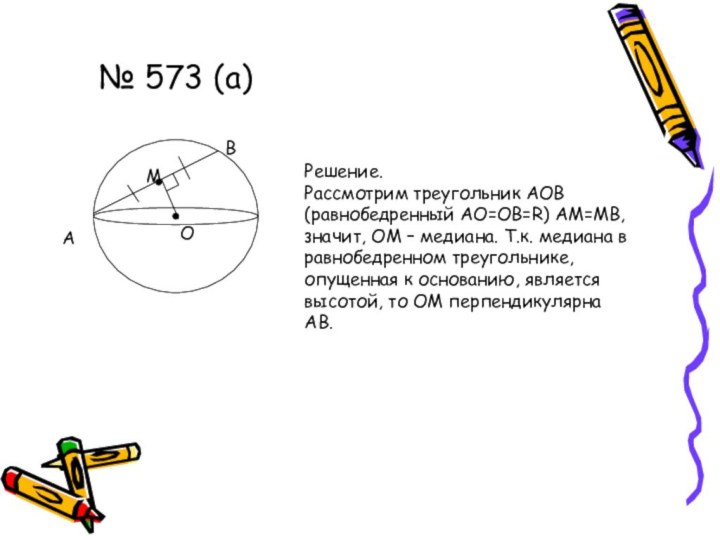
- 7. № 573 (а)АМВОРешение.Рассмотрим треугольник АОВ (равнобедренный АО=ОВ=R)
- 8. № 577 (а)Ответ (x+ 2)²+(y- 2)²+z²= R²R²= (5+ 2)²+(0- 2)²+(-1-0)²= 49+4+1=54Уравнение сферы: (x+ 2)²+(y- 2)²+z²= 54
- 9. Скачать презентацию
- 10. Похожие презентации
Окружность – геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.






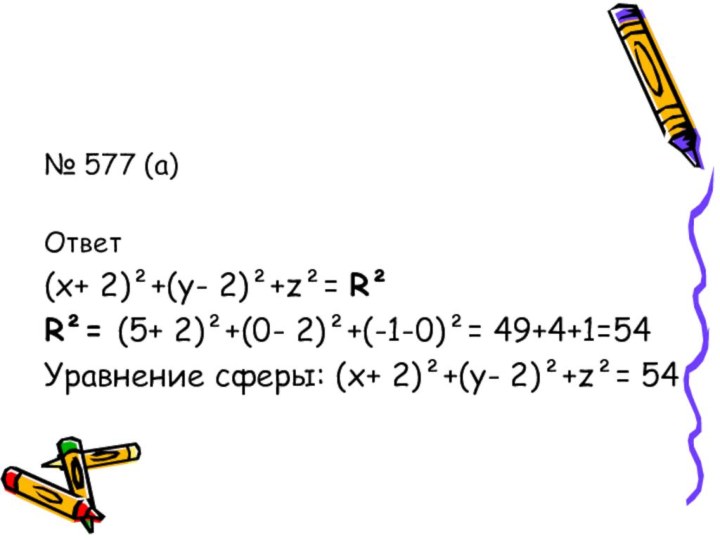

Слайд 3
Сфера –
поверхность, состоящая
из всех точек пространства, расположенных на данном расстоянии от данной точки.Слайд 4 Центром сферы является данная точка, в данном случаи
точка О.
Радиусом сферы является любой отрезок, соединяющий центр и
какую-нибудь точку сферы.Диаметром сферы является отрезок, соединяющий две точки сферы и проходящий через её центр. (=2R)