- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии по теме Многогранники(часть 2), 10 класс
Содержание
- 2. Звездчатые многогранники
- 3. Многогранник –
- 4. Звёздчатый многогранник — это
- 5. Звёздчатые многогранники Правильные — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники
- 6. Звёздчатые многогранники ПравильныеКубТетраэдр
- 7. Звёздчатые многогранники Полуправильные — многогранники, гранями которых являются правильные или звёздчатые многоугольники, но не обязательно одинаковые
- 8. Звёздчатые многогранники Полуправильные Усеченный тетраэдрУсеченный октаэдр
- 9. Звёздчатые многогранники Однородные — правильные и полуправильные
- 10. Однородные многогранники Платоновы телаАрхимедовы телаПять уникальных
- 11. Тетраэдр и куб Не
- 12. Октаэдр Существует только одна звёздчатая форма. Stella octangula — звезда восьмиугольная
- 13. Додекаэдр У большого додекаэдра гранями являются пятиугольники
- 14. Имеет три звёздчатые формы - малый звёздчатый додекаэдр;- большой додекаэдр;- большой звёздчатый додекаэдр.
- 15. Любая из звёздчатых форм
- 16. Икосаэдрсоединение пяти октаэдров;- соединение пяти тетраэдров;- соединение десяти тетраэдров.
- 17. Кубооктаэдр Имеет 4 звёздчатые формы
- 18. Многогранники в снежинках Снег возникает, когда
- 19. Из-за особой структуры молекул воды возможны углы лишь в 60° и 120°
- 20. Множество многогранников и Платоновых тел
- 21. Евграф Федоров10.12.1853 – 21.05.1919 гг.— русский академик
- 22. В 1890 году
- 23. Зеркальная симметрия
- 24. Поворотная симметрия
- 25. Многогранники в биологии Феодария –
- 26. Из 12
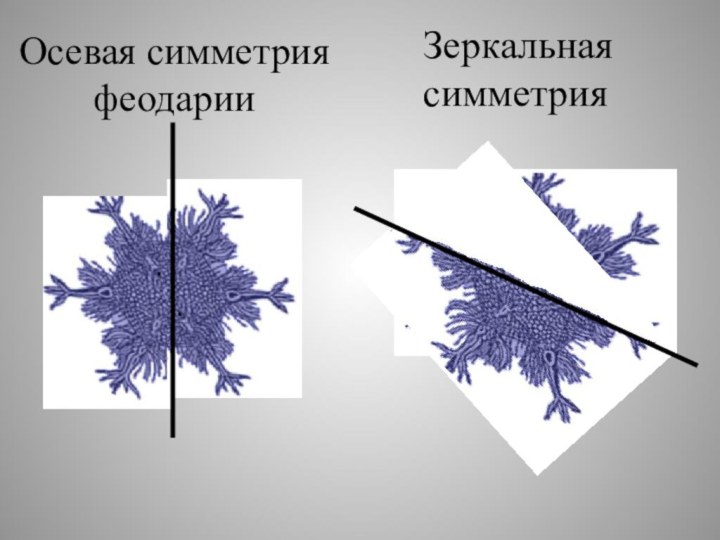
- 27. Осевая симметрия феодарииЗеркальная симметрия
- 28. Из всех многогранников
- 29. Бактерии можно
- 30. Аденовирусы
- 31. Внешняя оболочка аденовируса имеет
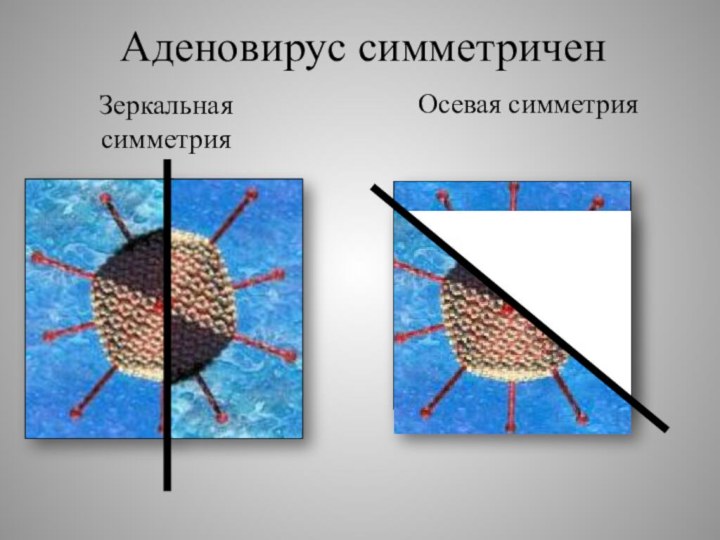
- 32. Аденовирус симметричен Ось
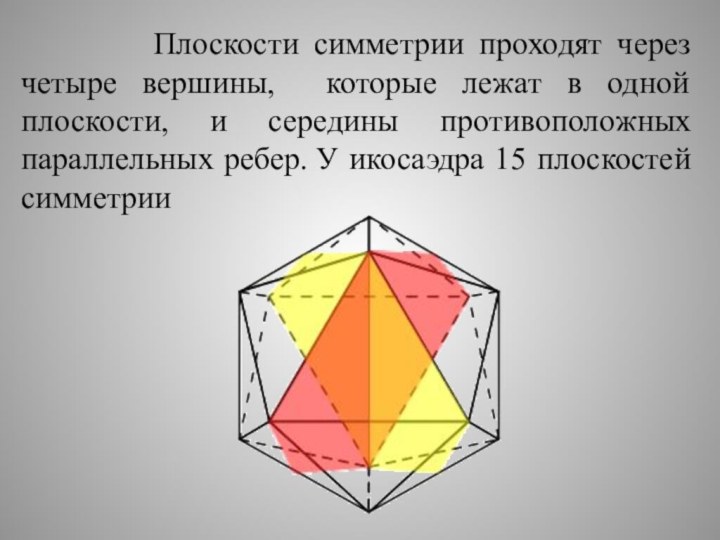
- 33. Плоскости симметрии
- 34. Аденовирус симметричен Зеркальная симметрияОсевая симметрия
- 36. Модель молекулы ДНК из многогранниковДодекаэдр Икосаэдр
- 37. Вывод В ходе нашего
- 38. Симметрия кристаллов
- 39. Симметрия кристаллов – свойство кристаллов совмещаться с
- 40. Точечные группы симметрии кристаллов Точечные группы симметрии -
- 41. В элементарной ячейке может содержаться один атом
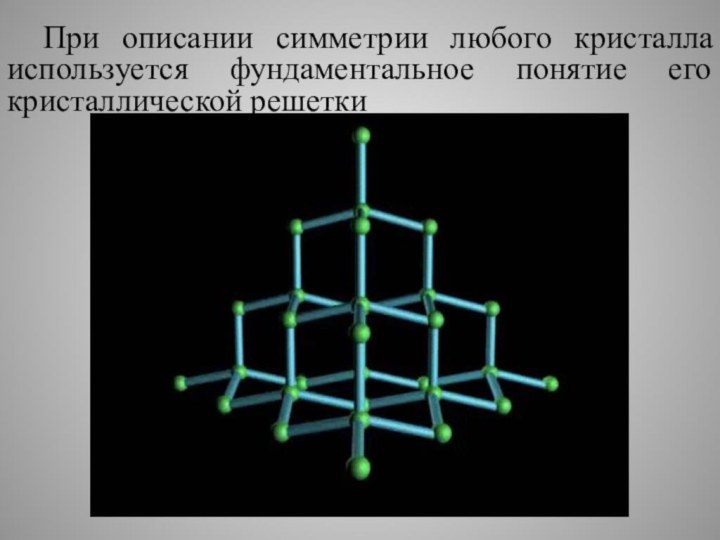
- 42. При описании симметрии любого кристалла используется фундаментальное понятие его кристаллической решетки
- 43. Преобразования симметрии объекта – пространственные перемещения,
- 44. Идеальный кристалл Идеальный кристалл
- 45. Исследование Мы решили воссоздать идеальный кристалл на
- 46. Выращивание кристаллаДень 1Вторая неделя
- 47. Моделирование кристаллаВ процессе моделирования мы использовали:-программу «3D Crafter»;-теоретические основы кристаллографии;-природный кристалл
- 48. 3D модель кристалла
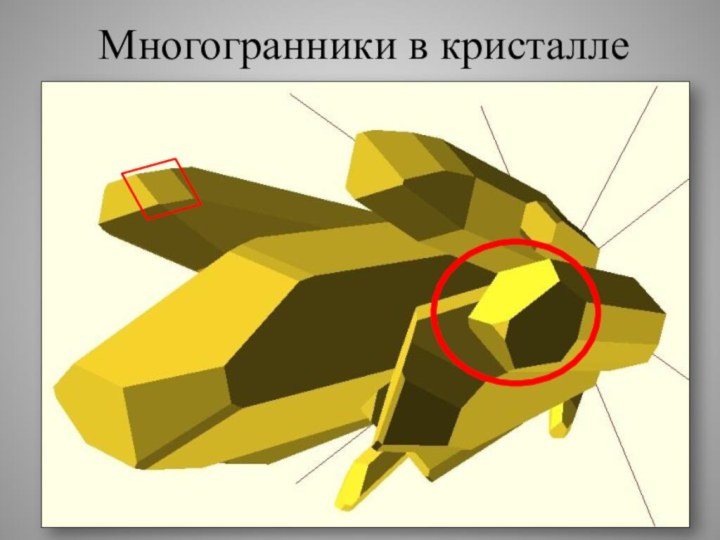
- 49. Многогранники в кристалле
- 50. Многогранники в кристалле
- 51. Многогранники в кристаллах Элементарная
- 52. Многогранники в кристаллах Кристаллическая
- 53. Многогранники на 3D модели На 3D модели мы обнаружили огромное количество многогранников:усеченный тетраэдр;треугольник;параллелограмм;прямоугольник;икосаэдр;усеченный октаэдр
- 54. Симметрия кристалла Поворот
- 55. Симметрия кристалла Отражение
- 56. Вывод В ходе нашей работы мы выявили, что
- 57. Многогранник Дюрера
- 58. «Меланхолия» — резцовая гравюра на меди
- 59. — немецкий живописец и график, один
- 60. Символы в гравюре Считается, что на гравюре изображен автопортрет Дюрера и присутствует разделение на три яруса
- 61. Первый ярусРемесленный уровень, к которому относятся такие предметы ремесла, как рубанки, инструменты, идеально выточенный шар
- 62. Второй ярусИнтеллектуальное познание – циркуль, весы, песочные часы, магический квадрат
- 63. Третий ярусТретий ярус — непознаваемого и божественного.
- 64. На заднем плане, позади центрального персонажа картины,
- 65. Форма камня рукотворна. Рядом с многогранником
- 66. Многогранник Дюрера является выпуклым, состоит из
- 67. Шесть из восьми углов лежат на
- 68. ПроекцииДоктор Эрнст Теодор Майер заметил, что проекция
- 69. Звезда ДавидаЗвезда Давида — древний символ, эмблема
- 70. Звезда Давида олицетворяет все четыре первоосновы: огонь
- 71. Магический квадратМагический, или волшебный квадрат — это
- 72. Магический квадрат 4×4, изображённый на гравюре,
- 73. Симметрия в многограннике Дюрера
- 74. Пятиугольные боковые грани многогранника ДюрераВ результате отсечения
- 75. Свойства пятиугольных боковых граней многогранника Дюрера
- 76. Диагонали образуют со стороной а равнобедренную трапецию, ось которой не совпадает с осью пятиугольника
- 77. Вывод Многогранники присутствуют и
- 78. В ходе исследования мы изучили и исследовали
- 79. Вывод Мы доказали, что многогранники являются
- 80. Скачать презентацию
- 81. Похожие презентации
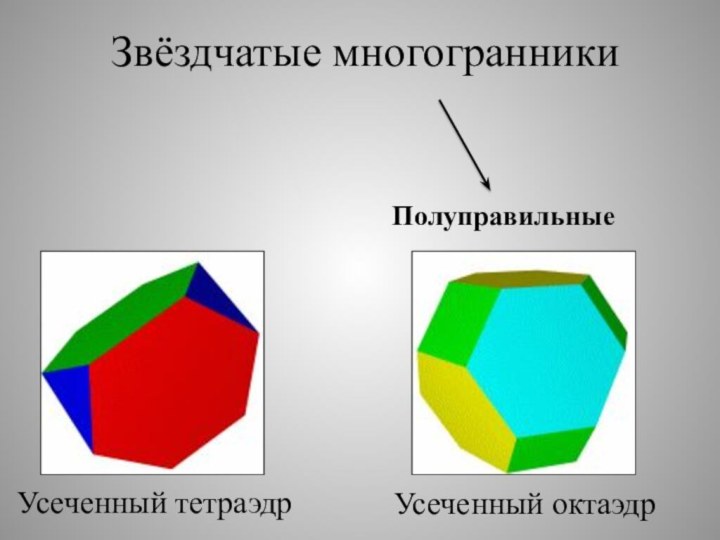
Звездчатые многогранники































































Слайд 3
Многогранник – это
тело, поверхность которого состоит из конечного числа плоских многоугольников
Слайд 4
Звёздчатый многогранник — это
невыпуклый многогранник, грани которого пересекаются между собой. Как и
у незвёздчатых многогранников грани попарно соединяются в рёбрах
Слайд 5
Звёздчатые многогранники
Правильные — это звёздчатые многогранники, гранями
которых являются одинаковые правильные или звёздчатые многоугольники
Слайд 7
Звёздчатые многогранники
Полуправильные — многогранники, гранями которых являются
правильные или звёздчатые многоугольники, но не обязательно одинаковые
Слайд 9
Звёздчатые многогранники
Однородные — правильные и полуправильные выпуклые
многогранники. У этих тел все грани являются правильными многоугольниками,
а все вершины одинаковы
Слайд 10
Однородные многогранники
Платоновы тела
Архимедовы тела
Пять уникальных форм. Грани
Платоновых тел - правильные многоугольники одного типа
Полуправильные однородные выпуклые
многогранники
Слайд 11
Тетраэдр и куб
Не имеют звёздчатых
форм, так как их грани при продлении через рёбра
не пересекаются
Слайд 14
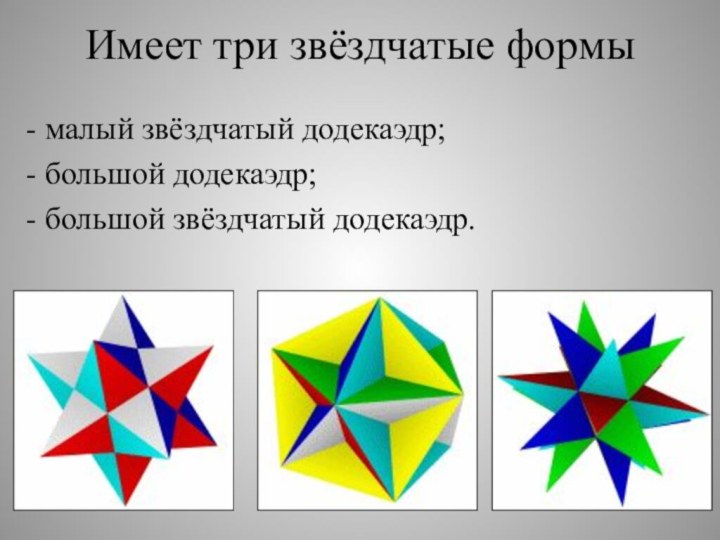
Имеет три звёздчатые формы
- малый звёздчатый додекаэдр;
-
большой додекаэдр;
- большой звёздчатый додекаэдр.
Слайд 15
Любая из звёздчатых форм
додекаэдра не является соединением платоновых тел, а образует новый
многогранник.У малого звёздчатого и большого звёздчатого додекаэдров гранями являются пятиконечные звёзды (пентаграммы)
Слайд 16
Икосаэдр
соединение пяти октаэдров;
- соединение пяти тетраэдров;
- соединение десяти
тетраэдров.
Слайд 18
Многогранники в снежинках
Снег возникает, когда микроскопические
капли воды в облаках притягиваются к пылевым частицам и
замерзают.Появляющиеся при этом кристаллы льда падают вниз и растут в результате конденсации на них влаги из воздуха
Слайд 21
Евграф Федоров
10.12.1853 – 21.05.1919 гг.
— русский академик РАН,
кристаллограф, минералог и математик. Народоволец.
Директор петербургского Горного института
Слайд 22
В 1890 году вывел
все геометрические законы сочетания элементов симметрии в кристаллических структурах
Показал, что имеется 230 пространственных групп симметрии
Слайд 25
Многогранники в биологии
Феодария – одноклеточный
организм, обитающий на морских глубинах, служит добычей коралловых рыб
Слайд 26
Из 12
вершин скелета выходят 12 полых игл. На концах игл
находятся зубцы, делающие иглу еще более эффективной при защите
Слайд 28
Из всех многогранников с
тем же числом граней именно икосаэдр имеет наименьший объем
при наибольшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи
Слайд 29
Бактерии можно представить
в виде звездчатых многогранников. Такое строение говорит о плотном
расположении тканей бактерии, что позволяет ей перемещаться внутри организмовЗвездчатая форма
додекаэдра
Слайд 30
Аденовирусы –
большая группа ДНК-содержащих вирусов, вызывающие простудные заболевания, являются перспективными объектами
для разработки медицинских технологий и средств генной терапии
Слайд 31
Внешняя оболочка аденовируса имеет
форму икосаэдра со скругленными рёбрами.
В
каждой вершине имеется выступающая белковая структура, необходимая для связывания с клеточными рецепторами
Слайд 32
Аденовирус симметричен
Ось
симметрии икосаэдра проходит через середины противолежащих параллельных ребер. Точка пересечения
осей икосаэдра – это и есть его центр симметрии. У икосаэдра 15 осей симметрии
Слайд 33
Плоскости симметрии
проходят через четыре вершины, которые лежат в одной плоскости,
и середины противоположных параллельных ребер. У икосаэдра 15 плоскостей симметрии
Слайд 35
Молекула ДНК представляет собой вращающийся куб. При повороте
куба последовательно на 72° по определённой модели, получается икосаэдр.Двойная нить спирали ДНК построена по принципу двухстороннего соответствия: за икосаэдром следует додекаэдр, затем опять икосаэдр. Это вращение через куб создаёт молекулу ДНК
Слайд 37
Вывод
В ходе нашего исследования
мы выяснили, что с помощью многогранников можно научиться строить
биологические модели, а также выяснили, что многогранники встречаются в окружающем нас мире чаще, чем мы думаем
Слайд 39
Симметрия кристаллов – свойство кристаллов совмещаться с собой
при поворотах, отражениях, параллельных переносах, либо при части или
комбинации этих операций. Симметрия внешней формы кристалла определяется симметрией его атомного строения, которая обуславливает также и симметрию физических свойств кристалла
Слайд 40
Точечные группы симметрии кристаллов
Точечные группы симметрии - группы
симметрии, операции которых оставляют хотя бы одну точку пространства
на местегруппа линейных преобразований;
группа вращений;
зеркальная симметрия
Слайд 41 В элементарной ячейке может содержаться один атом (примитивная
ячейка), или больше одного (сложная ячейка).
В общем случае элементарная ячейка имеет форму параллелепипеда и характеризуется параметрами: длина ребер a, b, c;
углы между ребрами α, β, γ
Слайд 42 При описании симметрии любого кристалла используется фундаментальное понятие
его кристаллической решетки
Слайд 43 Преобразования симметрии объекта – пространственные перемещения, совмещающие
его самим собой.
Для кристаллических структур имеются 32 точечные
группы и 230 пространственных групп
Слайд 44
Идеальный кристалл
Идеальный кристалл —
это математический объект, имеющий полную, свойственную ему симметрию, идеализированно
ровные гладкие грани.Идеальный кристалл можно построить путем бесконечного повторения в пространстве его структурной единицы (элементарной ячейки)
Слайд 45
Исследование
Мы решили воссоздать идеальный кристалл на примере
природного при помощи моделирования и проверить его свойства симметрии
с использованием его объемной модели
Слайд 47
Моделирование кристалла
В процессе моделирования мы использовали:
-программу «3D Crafter»;
-теоретические
основы кристаллографии;
-природный кристалл
Слайд 51
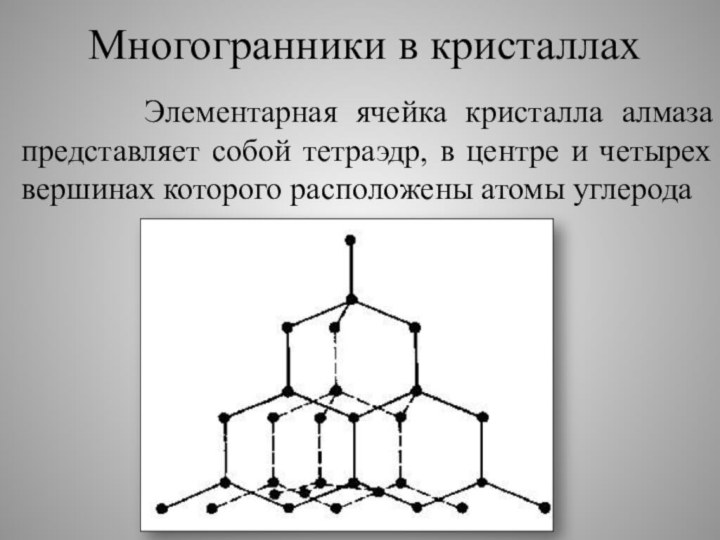
Многогранники в кристаллах
Элементарная ячейка
кристалла алмаза представляет собой тетраэдр, в центре и четырех
вершинах которого расположены атомы углерода
Слайд 52
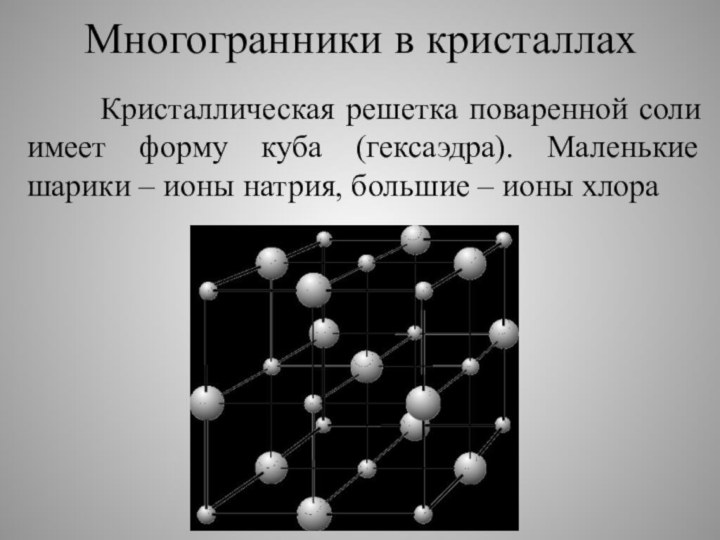
Многогранники в кристаллах
Кристаллическая решетка
поваренной соли имеет форму куба (гексаэдра). Маленькие шарики –
ионы натрия, большие – ионы хлора
Слайд 53
Многогранники на 3D модели
На 3D модели мы
обнаружили огромное количество многогранников:
усеченный тетраэдр;
треугольник;
параллелограмм;
прямоугольник;
икосаэдр;
усеченный октаэдр
Слайд 56
Вывод
В ходе нашей работы мы выявили, что идеальные
кристаллы имеют геометрически правильное внутреннее строение и образованы в
виде выпуклых многогранников с плоскими гранями и прямыми рёбрами
Слайд 58
«Меланхолия» — резцовая гравюра на меди немецкого
художника Альбрехта Дюрера, законченная в 1514 году. Является одной
из наиболее известных работ Дюрера, и выделяется сложностью и неочевидностью идеи, яркостью символов и аллегорий
Слайд 59
— немецкий живописец и график, один из
величайших мастеров западноевропейского Ренессанса.
Изучал проблемы перспективы,
занимался теоретическими вопросами изобразительного искусства1471—1528гг.
Альбрехт Дюрер
Слайд 60
Символы в гравюре
Считается, что на гравюре изображен
автопортрет Дюрера и присутствует разделение на три яруса
Слайд 61
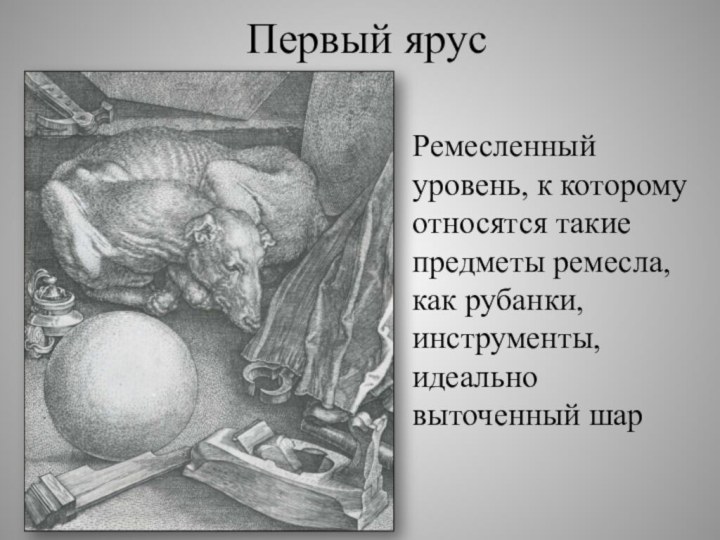
Первый ярус
Ремесленный уровень, к которому относятся такие предметы
ремесла, как рубанки, инструменты, идеально выточенный шар
Слайд 63
Третий ярус
Третий ярус — непознаваемого и божественного. Лестница
уходит в небо, за край гравюры, как и башня,
у подножия которой сидит АнгелСлайд 64 На заднем плане, позади центрального персонажа картины, каменный
многогранник, сложной формы - композиционно уравновешивающий плечистую фигуру "Крылатого
Гения"
Слайд 65
Форма камня рукотворна. Рядом с многогранником молоток.
На гранях камня небольшие сколы.
Исследователи считают, что многогранник
состоит из обработанного флюорита, куска плавикового шпата
Слайд 66
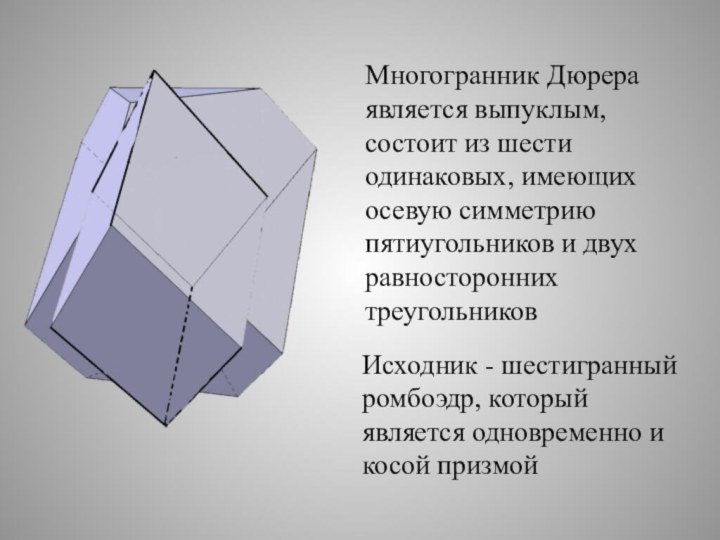
Многогранник Дюрера является выпуклым, состоит из шести
одинаковых, имеющих осевую симметрию пятиугольников и двух равносторонних треугольников
Исходник - шестигранный ромбоэдр, который является одновременно и косой призмой
Слайд 67
Шесть из восьми углов лежат на общей
описанной сфере, два пика выступают за пределы сферы.
При
отсечении пиков на одинаковой высоте в каждом случае появляются три новых угла
Слайд 68
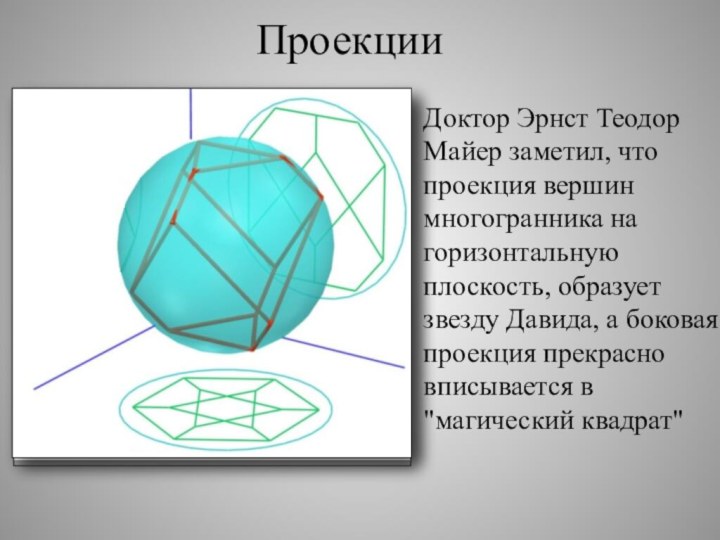
Проекции
Доктор Эрнст Теодор Майер заметил, что проекция вершин
многогранника на горизонтальную плоскость, образует звезду Давида, а боковая
проекция прекрасно вписывается в "магический квадрат"
Слайд 69
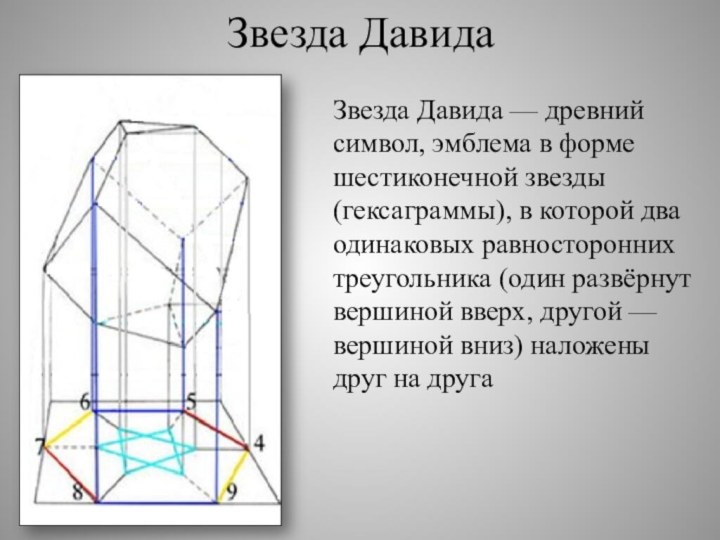
Звезда Давида
Звезда Давида — древний символ, эмблема в
форме шестиконечной звезды (гексаграммы), в которой два одинаковых равносторонних
треугольника (один развёрнут вершиной вверх, другой — вершиной вниз) наложены друг на другаСлайд 70 Звезда Давида олицетворяет все четыре первоосновы: огонь и
воздух, воду и землю. Верхний угол одного из треугольников
символизирует огонь, два других — воду и воздух
Слайд 71
Магический квадрат
Магический, или волшебный квадрат — это квадратная
таблица n x n (в данном случает 4х4), заполненная
числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова
Слайд 72
Магический квадрат 4×4, изображённый на гравюре, считается
самым ранним в европейском искусстве.
Два средних числа в
нижнем ряду указывают дату создания гравюры (1514). Сумма чисел на любой горизонтали, вертикали и диагонали равна 34
Слайд 74
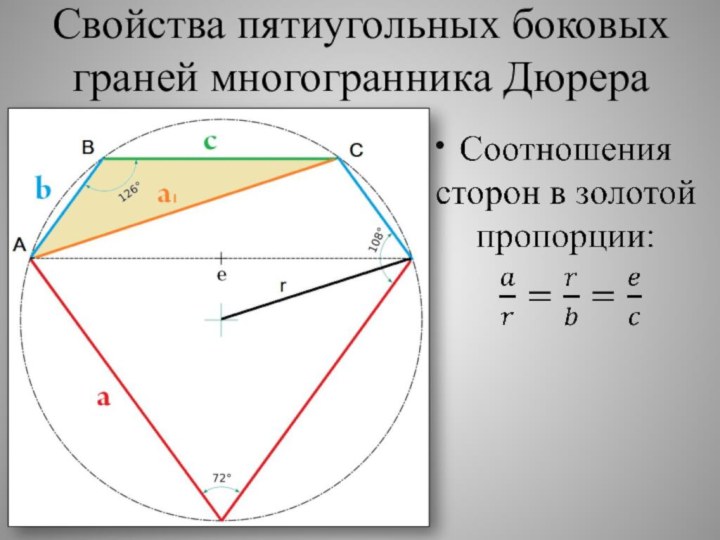
Пятиугольные боковые грани многогранника Дюрера
В результате отсечения ромбовидные
грани многогранника Дюрера становятся пятиугольникам. Две грани пятиугольника остаются
нетронутыми с углом 72° между ними, два других тупых угла равны 126°126°
Слайд 76
Диагонали образуют со стороной а равнобедренную трапецию,
ось которой не совпадает с осью пятиугольника
Слайд 77
Вывод
Многогранники присутствуют и в
искусстве, играя важную роль в понимании смысла произведений. Каждый
их элемент, каждый признак несет символическую нагрузку
Слайд 78
В ходе исследования мы
изучили и исследовали историю изменения
и развития понятия многогранника;
рассмотрели виды симметрии многогранников;
смоделировали «идеальный» дом
и идеальный кристалл;сконструировали модель ДНК;
нашли виды звездчатых многогранников в живой и «неживой» природе;
обнаружили многогранники в искусстве и интерпретировали их символическую роль