- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Паркеты на плоскости
Содержание
- 2. Цель работы – подробно изучить паркеты.
- 3. Задачи
- 4. Паркеты
- 5. Паркеты на плоскости
- 6. Паркет называется правильным, если он состоит из равных правильных многоугольников.
- 7. Паркет из квадратов
- 8. Простой паркет из правильных треугольников.
- 9. Паркет из правильных шестиугольников
- 10. Паркеты из квадратов и треугольников
- 11. В одной вершине сходятся три правильных треугольника и два квадрата.
- 12. В одной вершине сходятся четыре треугольника и шестиугольник.
- 13. В одной вершине сходятся два треугольника и два шестиугольника.
- 14. Паркет, состоящий из квадратов и восьмиугольников
- 15. Паркет из треугольников и двенадцатиугольников.
- 16. В каждой вершине сходятся шестиугольник, треугольник и два квадрата.
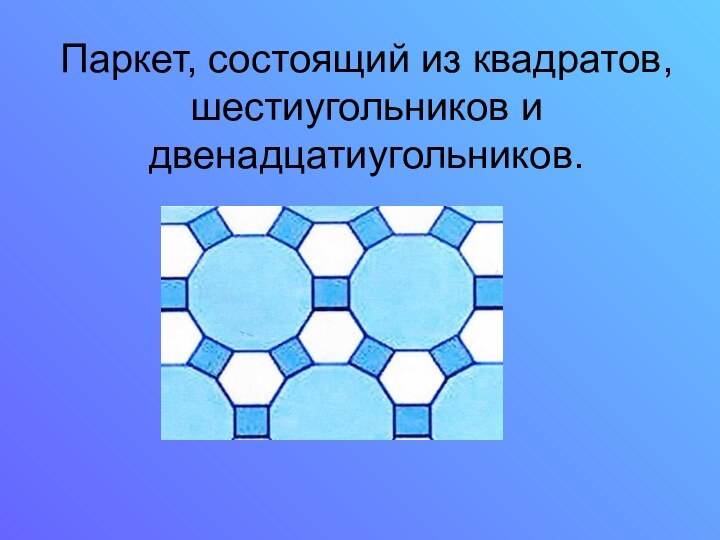
- 17. Паркет, состоящий из квадратов, шестиугольников и двенадцатиугольников.
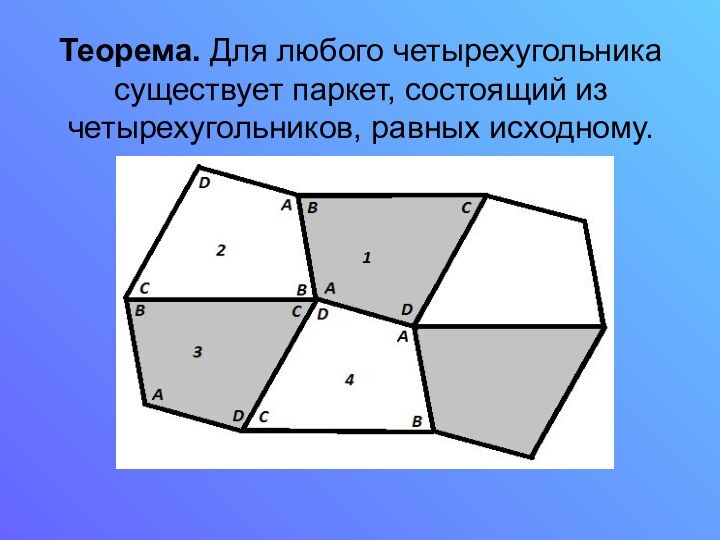
- 18. Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников, равных исходному.
- 19. Паркет из параллелограммов.
- 20. Паркет из произвольных четырехугольников
- 21. Паркет из криволинейных плиток.
- 22. Спиральное замощение плоскости девятиугольниками
- 23. Квазипериодические паркеты
- 24. Мариус Корнелис Эшер (1898-1972) Он
- 25. Скачать презентацию
- 26. Похожие презентации
Цель работы – подробно изучить паркеты.