Презентация на тему Сферические координаты

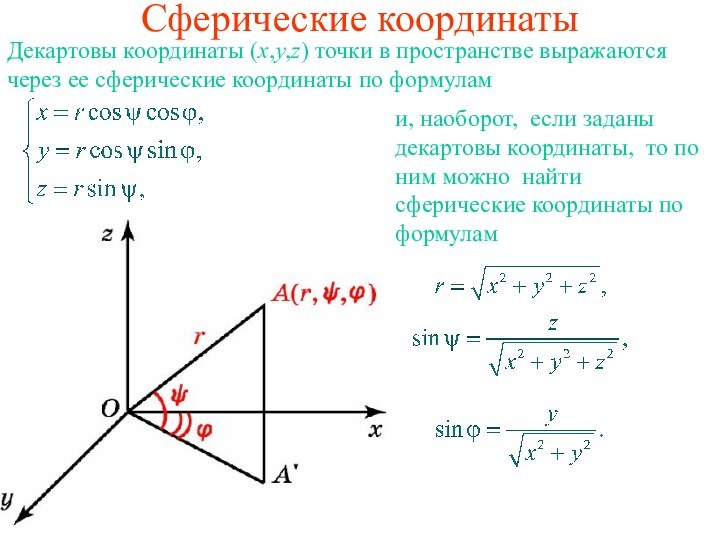
через ее сферические координаты по формулам
и, наоборот, если заданы

образуют окружность, которая называется параллелью. Точки, имеющие одинаковый угол

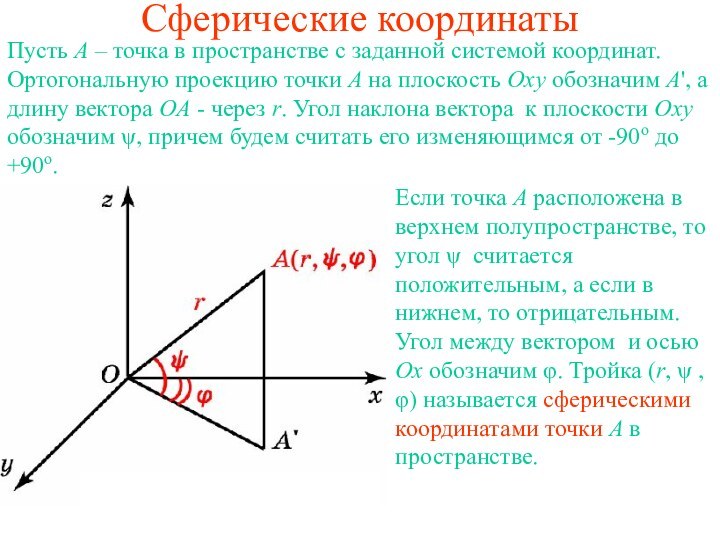
Дуга большой окружности, соединяющая две точки сферы, является кратчайшим путем на сфере между этими двумя точками. Такой путь называют ортодромией, что в переводе с греческого означает "прямой бег".

Кривая, образующая равные углы с разными меридианами, называется локсодромия, что в переводе с греческого означает "косой бег".

координаты следующих точек пространства, заданных своими сферическими координатами: (1,45°,120°),

координаты следующих точек пространства, заданных своими декартовыми координатами: A(1,1,1),

координаты вершин куба, задаваемого в декартовых координатах системой неравенств

имеет сферические координаты (r, ψ, ϕ). Найдите сферические координаты

Ответ: а) (r, -ψ, ϕ), (r, ψ, 180о-ϕ), (r, ψ, -ϕ);

б) (r, -ψ, -ϕ), (r, -ψ, 180о-ϕ), (r, ψ, 180о+ϕ);

в) (r, -ψ, 180о+ϕ).

место точек пространства, сферические координаты которых удовлетворяют условиям: а)

Ответ: а) Сфера;

б) коническая поверхность;

в) полуплоскость.

в пространстве задается неравенствами: а) 0 ≤ r ≤

Ответ: а) Полушар;

б) полушар;

в) четверть шара.

между точками, заданными своими сферическими координатами: A(

Ответ: 2.

локсодромия, образующая острый угол с меридианами, при ее продолжении

Ответ: На полюсах.

сферы в сферических координатах
Ответ: r = 1.