- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площади многоугольников
Содержание
- 2. Цель: Развить и закрепить понятие площади многоугольников.
- 3. Историческая справка Возникновение геометрии уходит вглубь тысячелетий
- 4. Если не учитывать весьма малый вклад древних
- 5. Чтобы найти площадь треугольника,древние египтяне основание треугольника
- 6. Задачи, в которых требуется определить условия, при
- 7. Геометрические задачи, в которых отыскивается фигура с
- 8. гораздо большую площадь по сравнению с той,
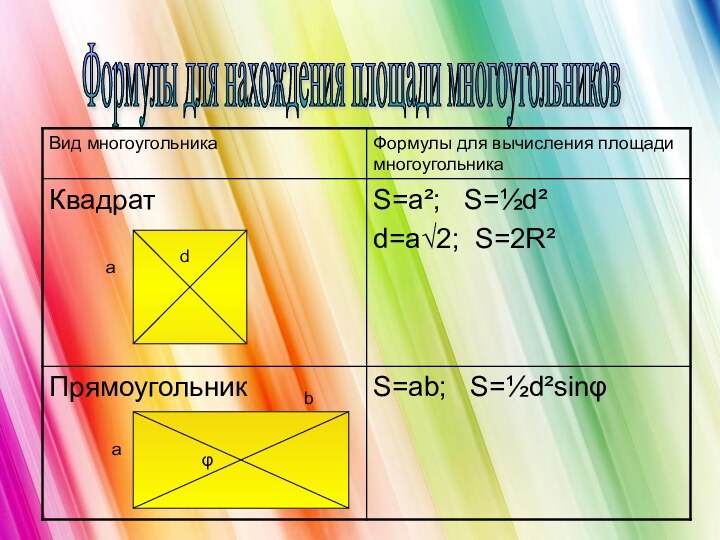
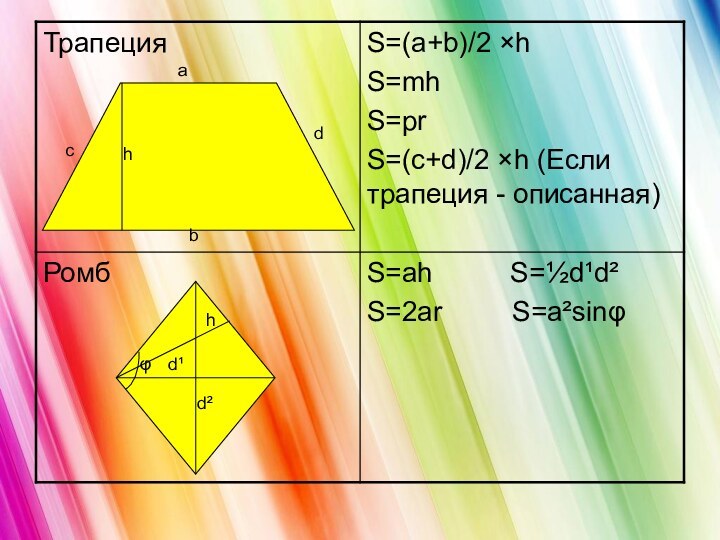
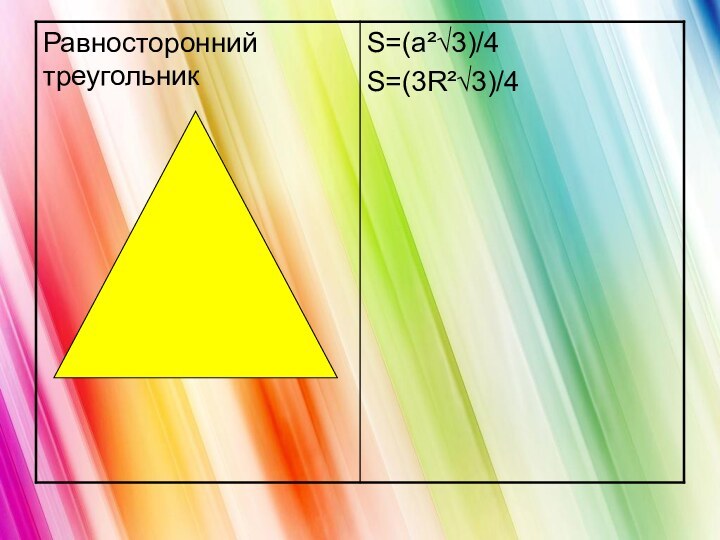
- 9. Формулы для нахождения площади многоугольников adаbφ
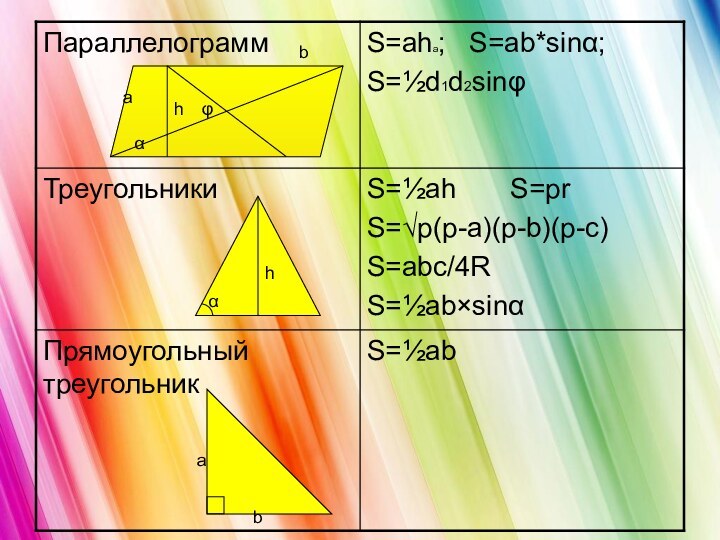
- 10. abhαφhαab
- 11. habd¹d²φhcd
- 13. ЗадачаВ одном городе стоит телевизионная башня,свет которой
- 14. 1. Чему равна площадь прямоугольника?
- 15. 7. Площадь трапеции 210 см². Высота 10
- 17. БББАБББВАААбТЕСТ
- 18. Скачать презентацию
- 19. Похожие презентации
Цель: Развить и закрепить понятие площади многоугольников.













Слайд 4
Если не учитывать весьма малый вклад древних обитателей
долины между Тигром и Евфратом, и Малой Азии, то
геометрия зародилась в Древнем Египте где-то в 1700 году до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложениянужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянам стали такие виды их деятельности, как возведение пирамид и изобразительное искусство.
Способы вычисления площади дошли до нас в папирусах.Среди них наиболее известные-папирус Ринда(около 1800 г.до н.э.),содержащий 84 задачи с решениями,и так называемый московский папирус(около 1600 г. до н.э.),он содержит 25 задач.
Слайд 5
Чтобы найти площадь треугольника,древние египтяне основание треугольника делили
пополам и умножали на высоту.А для отределения площади равнобедренного
треугольника использовали полупроизведение его боковых сторон.
Слайд 6
Задачи, в которых требуется определить условия, при которых
некоторая величина принимает наибольшее или наименьшее значение, принято называть
задачами “на экстремум” (от лат. слова extremum – “крайний”) или задачами “на максимум и минимум” (от латинских maximum и minimum –соответственно “наибольшее” и “наименьшее”). Такие задачи очень часто встречаются в технике и естествознании, в повседневной практической деятельности людей. Из всех геометрических задач на экстремум считается самой простой и самой древней: “Какой из всех прямоугольников заданного периметра имеет наибольшую площадь?”. Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в VI книге “Начал” Евклида, где доказывается, что, если рассмотреть прямоугольник и квадрат одного и того же периметра, то площадь квадрата будет больше. Доказательство основано на сравнении площадей. Площадь прямоугольника равна , а площадь квадрата и , если . Таким образом, получили, что из всех прямоугольников с заданным периметром наибольшую площадь имеет квадрат.В решении Евклида, во-первых, указан ответ (квадрат) и, во-вторых, доказано, что по площади он превосходит все другие возможные фигуры (прямоугольники заданного периметра). Именно так понимают в математике решения задачи на экстремум: дать ответ и доказать его экстремальное свойство.
ЗАДАЧИ ЦАРИЦЫ ДИДОРЫ
Слайд 7
Геометрические задачи, в которых отыскивается фигура с экстремальным
свойством среди других фигур с равным периметром, называются изопериметрическими.
Такие задачи рассматривал древнегреческий математик Зенодор (II-I вв. до н.э.). Например, Зенодор утверждал, что:1) из всех многоугольников с равным периметром и равным числом сторон наибольшую площадь имеет правильный многоугольник;
2) из двух правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше;
3) из всех плоских фигур с равным периметром наибольшую площадь имеет круг.
Строгое доказательство третьего утверждения Зенодора было доказано только в XVIII веке знаменитым математиком Л. Эйлером.
Изопериметрические задачи известны также под названием “задачи Дидоны” по имени легендарной основательницы города Карфагена и его первой царицы. Согласно легенде, вынужденная бежать из своего родного города, царица Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей место для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узенькие ремешки и, разложив их , сумела ограничить
Слайд 8
гораздо большую площадь по сравнению с той, которую
можно было бы покрыть шкурой целиком. Если учесть, что
Дидона выбирала участок, примыкающий к берегу морю, то на языке математике задачу, стоящую перед Дидоной можно сформулировать так: какой формы должна быть кривая длины l, чтобы площадь фигуры, ограниченная этой кривой и заданной линией Г, была наибольшей.
Слайд 13
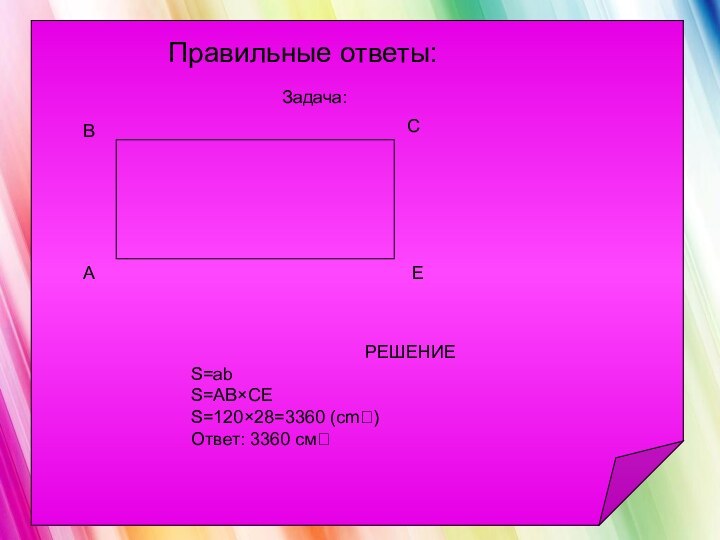
Задача
В одном городе стоит телевизионная башня,
свет которой можно
увидеть с последнего этажа
высотного дома, на расстоянии 120 м.
Высота
башни равна высоте многоэтажного дом и составляет 28 м.Какую фигуру можно получить
соединяя точки в вершинах и в началах зданий?
Какова площадь полученной фигуры?
Слайд 14
1. Чему равна площадь прямоугольника?
а)
S=ah б)S=ab
2. Сумма углов
n-угольника равна:а)180° б)180°(n-2)
3. Сумма всех внутренних и всех внешних углов n-угольника
Пропорциональна
а) количеству его углов б)количеству его вершин
4. По какой формуле вычисляется площадь трапеции?
а) S=mh б) S=½ab
5. По какой формуле вычисляется площадь прямоугольного
Треугольника?
а) S=mh б) S=½ab
6. По какой формуле вычисляется площадь ромба?
а) S=½ab б) S=ah
Тест
Слайд 15
7. Площадь трапеции 210 см². Высота 10 см.
Найдите среднюю линию
а)2,1см
б)21см в) 0,12см8. Площадь параллелограмма 1400см². Одна из его сторон
35см.Найдите высоту прилежащую к этой стороне.
а) 42см б)36см в) 40см
9. Дан прямоугольник. Две его стороны равны
Соответственно 15 и 34 см. Найдите площадь
а) 510см б) 505 см в) 450см
10. Дана трапеция описанная около окружности.
Боковые стороны трапеции равны 23 и 15 см. Высота 17см.
Найти площадь.
а) 323 см б)330см в) 400см
11.По какой формуле вычисляется полупериметр?
а) ½(а+б+с) б) а+б+с
12.По какой формуле вычисляется площадь вписанного
Квадрата?
а)R² б)2R²