- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Особая роль осевой симметрии
Содержание
- 2. Движение плоскости – отображение плоскости на себя, сохраняющая расстояние (центральная, осевая симметрия, параллельный перенос, поворот)
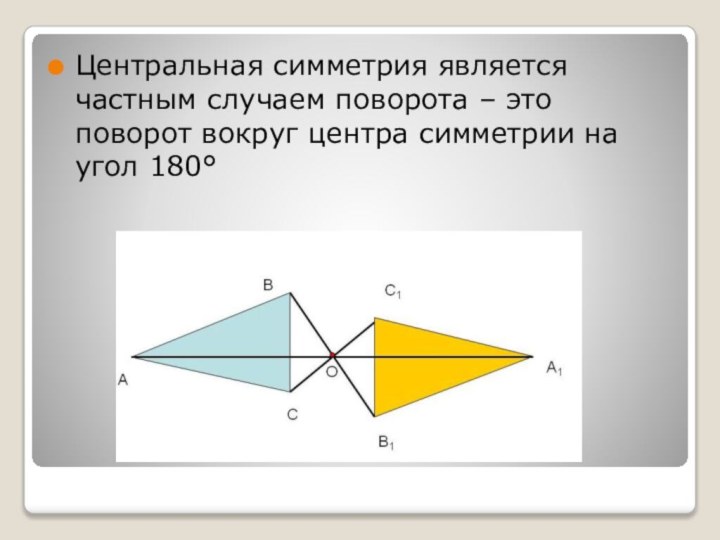
- 3. Центральная симметрия является частным случаем поворота – это поворот вокруг центра симметрии на угол 180°
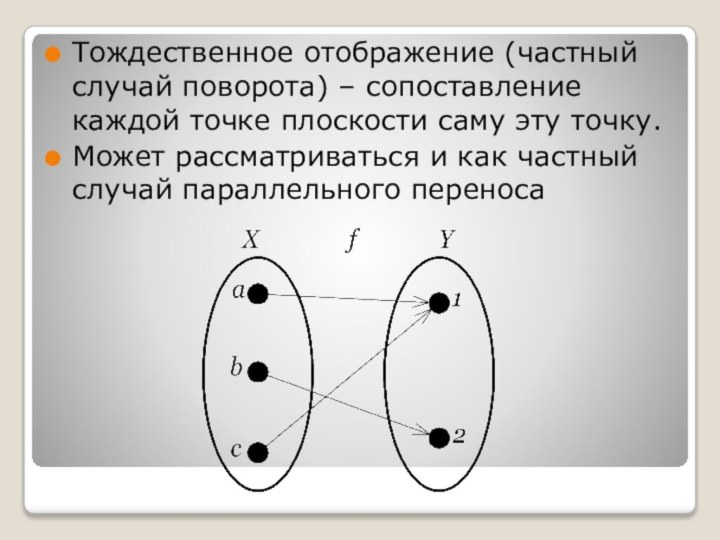
- 4. Тождественное отображение (частный случай поворота) – сопоставление
- 5. Последовательное выполнение двух движений даёт новое движение.Выясним,
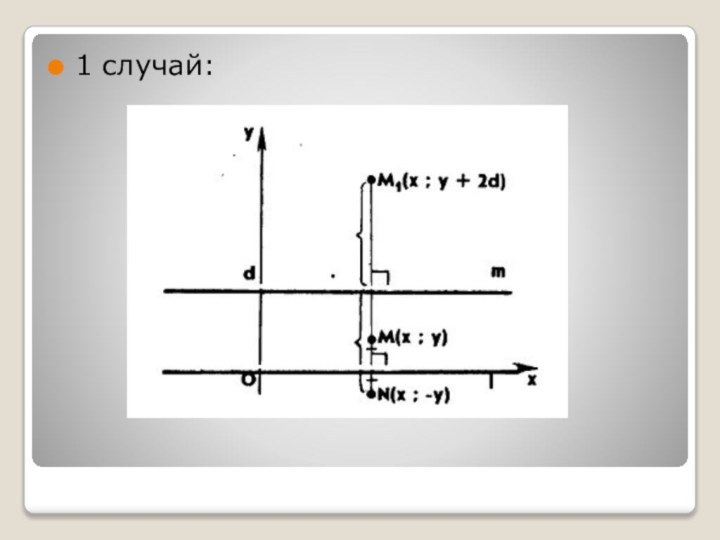
- 6. 1 случай:
- 7. Результатом последовательного выполнения двух осевых симметрий с
- 8. 2 случай:
- 9. Результатом последовательного выполнения двух осевых симметрий с
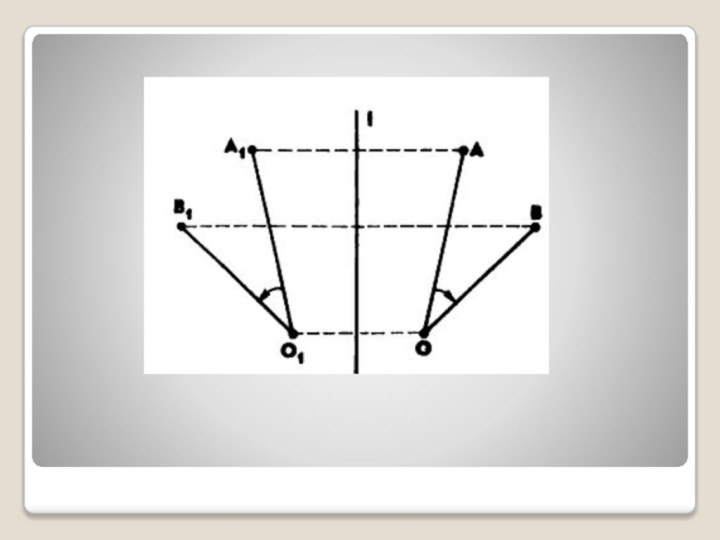
- 10. Частные случаи:Если l ⊥ m, то в
- 12. Осевая симметрия сохраняет величину угла, но меняет
- 13. Скачать презентацию
- 14. Похожие презентации
Движение плоскости – отображение плоскости на себя, сохраняющая расстояние (центральная, осевая симметрия, параллельный перенос, поворот)









Слайд 2 Движение плоскости – отображение плоскости на себя, сохраняющая
расстояние (центральная, осевая симметрия, параллельный перенос, поворот)
Слайд 3 Центральная симметрия является частным случаем поворота – это
поворот вокруг центра симметрии на угол 180°
Слайд 4 Тождественное отображение (частный случай поворота) – сопоставление каждой
точке плоскости саму эту точку.
Может рассматриваться и как частный
случай параллельного переноса
Слайд 5
Последовательное выполнение двух движений даёт новое движение.
Выясним, какое
движение получается в результате последовательного выполнения двух осевых симметрий
с различными осями l и mВозможны 2 случая:
l ||m
l ∩ m