Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Тригонометрические формулы

Содержание

Лекция № 5 Преобразование тригонометрических выражений(вывод тригонометрических формул)
Государственное Образовательное Учреждение Лицей №1523ЮАО г.МоскваЛекции по алгебре и началам анализа10 класс© Хомутова Лариса Юрьевна Лекция № 5 Преобразование тригонометрических выражений(вывод тригонометрических формул) I-a. Формулы приведения Выведем вспомогательные формулы, позволяющие находить и по ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. ∠A1OC = π / 2 ‑ ∠COA = ∠AOB; ΔAOB = Δ A1OC по гипотенузе и Покажем, что ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. Кроме того, на , . I-a. Формулы приведения II. Формулы сложения 0 II. Формулы сложения II. Формулы сложения I-b. Формулы приведения Выведенные формулы сложения позволяют получить формулы приведения, III. Формулы двойных углов Чтобы вывести формулы для вычисления тригонометрических III. Формулы двойных углов III. Формулы двойных углов III. Формулы двойных углов . IV. Формулы тройных углов . IV. Формулы тройных углов V. Формулы половинных углов. . ; V. Формулы половинных углов, ., . VI. Формулы преобразования произведения тригонометрических функций в сумму.Сложив почленно равенства (3) и VI. Формулы преобразования произведения тригонометрических функций в сумму VII. Формулы преобразования суммы тригонометрических функций в произведение . . . VII. Формулы преобразования суммы тригонометрических функций в произведение
Слайды презентации

Слайд 2 Лекция № 5
Преобразование тригонометрических выражений
(вывод тригонометрических формул)

Лекция № 5 Преобразование тригонометрических выражений(вывод тригонометрических формул)

Слайд 3 I-a. Формулы приведения
Выведем вспомогательные формулы,

I-a. Формулы приведения Выведем вспомогательные формулы, позволяющие находить и по тригонометрическим функциям угла α.

позволяющие находить
и
по тригонометрическим функциям угла

α.

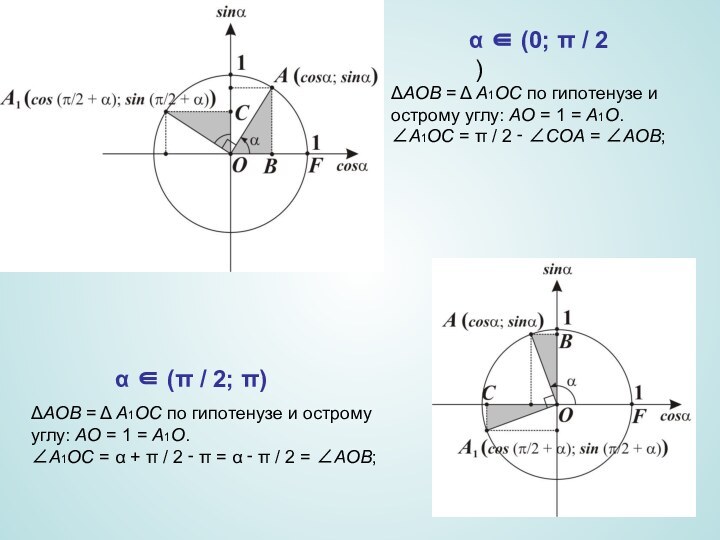
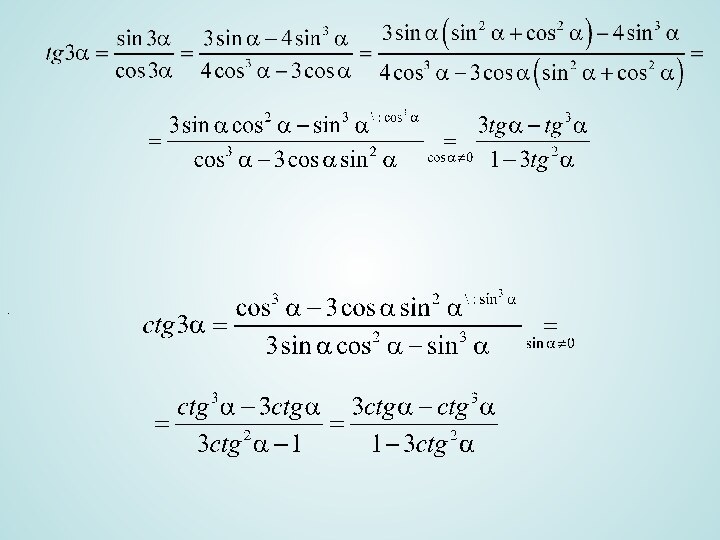
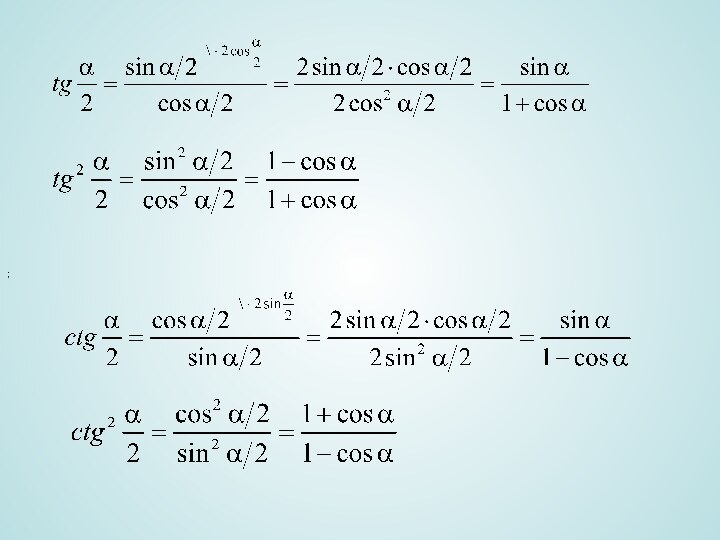
Слайд 4 ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. ∠A1OC = π / 2 ‑ ∠COA = ∠AOB;

ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. ∠A1OC = π / 2 ‑ ∠COA = ∠AOB; ΔAOB = Δ A1OC по гипотенузе


ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. ∠A1OC = α + π / 2 ‑ π = α ‑ π / 2 = ∠AOB;
α ∈ (0; π / 2 )
α ∈ (π / 2; π)

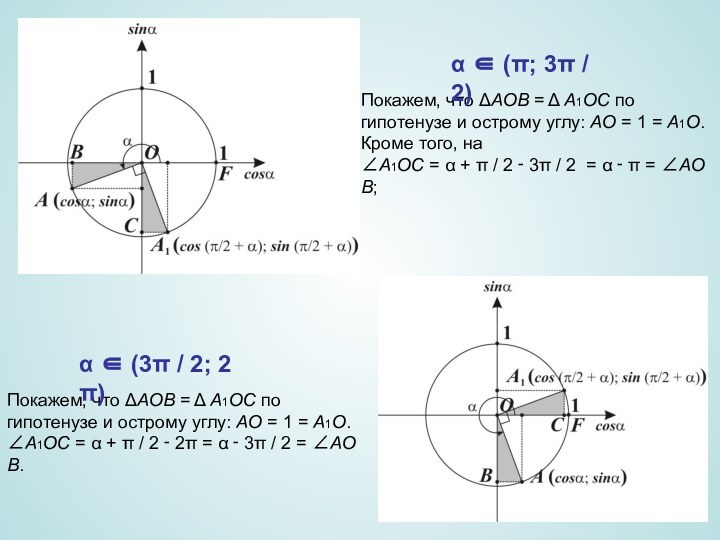
Слайд 5 Покажем, что ΔAOB = Δ A1OC по гипотенузе и острому углу:

Покажем, что ΔAOB = Δ A1OC по гипотенузе и острому углу: AO = 1 = A1O. Кроме того,

AO = 1 = A1O. Кроме того, на ∠A1OC = α + π / 2 ‑ 3π / 2  = α ‑ π = ∠AOB;
Покажем, что ΔAOB = Δ A1OC по

гипотенузе и острому углу: AO = 1 = A1O. ∠A1OC = α + π / 2 ‑ 2π = α ‑ 3π / 2 = ∠AOB.

α ∈ (π; 3π / 2)

α ∈ (3π / 2; 2π)

Слайд 6
,
.
I-a. Формулы приведения

, . I-a. Формулы приведения

Слайд 7 II. Формулы сложения





0















II. Формулы сложения 0

Слайд 8



Слайд 9

Слайд 10 II. Формулы сложения

II. Формулы сложения

Слайд 11

Слайд 12
II. Формулы сложения

II. Формулы сложения

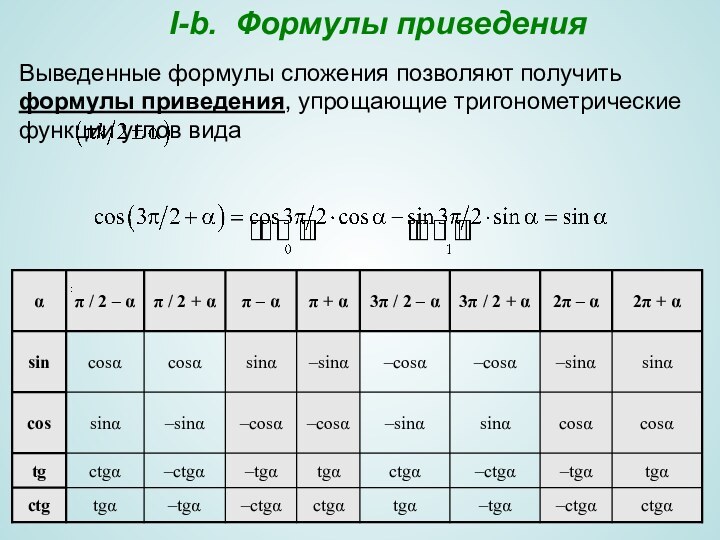
Слайд 13 I-b. Формулы приведения

Выведенные формулы сложения

I-b. Формулы приведения Выведенные формулы сложения позволяют получить формулы приведения,

позволяют получить формулы приведения, упрощающие тригонометрические функции углов вида


:

Слайд 14 III. Формулы двойных углов
Чтобы вывести

III. Формулы двойных углов Чтобы вывести формулы для вычисления тригонометрических

формулы для вычисления тригонометрических функций двойного аргумента, подставим β = α

в формулы сложения:

Слайд 15

III. Формулы двойных углов

III. Формулы двойных углов

Слайд 16

III. Формулы двойных углов

III. Формулы двойных углов

Слайд 17



Слайд 18 III. Формулы двойных углов




III. Формулы двойных углов

Слайд 19







.
IV. Формулы

. IV. Формулы тройных углов

тройных углов

Слайд 20

.

.

Слайд 21
IV. Формулы тройных углов




IV. Формулы тройных углов

Слайд 22 V. Формулы половинных углов

.

.


V. Формулы половинных углов. .

Слайд 23
;

;

Слайд 24
V. Формулы половинных углов



,
.

,
.

V. Формулы половинных углов, ., .

Слайд 25 VI. Формулы преобразования произведения тригонометрических функций в сумму

.
Сложив

VI. Формулы преобразования произведения тригонометрических функций в сумму.Сложив почленно равенства (3)

почленно равенства (3) и (4), получим:
.
Вычтя из равенства

(4) равенство (3), получим:

.

Слайд 26
VI. Формулы преобразования произведения тригонометрических функций в сумму



VI. Формулы преобразования произведения тригонометрических функций в сумму

Слайд 27 VII. Формулы преобразования суммы тригонометрических функций в произведение

VII. Формулы преобразования суммы тригонометрических функций в произведение .



.

Слайд 28

.


.

. .
  • Имя файла: trigonometricheskie-formuly.pptx
  • Количество просмотров: 175
  • Количество скачиваний: 0
- Предыдущая Кровотечения в последовом и раннем послеродовом периодах
Следующая - Овощи + фрукты + ягоды = здоровье

Похожие презентации

Возникновение и развитие геометрии Возникновение и развитие геометрии 185
Аксиомы стереометрии Аксиомы стереометрии 182
Метод золотого сечения Метод золотого сечения 163
Презентация Прямоугольный треугольник 7 класс Презентация Прямоугольный треугольник 7 класс 175
Презентация по геометрии на тему: Неравенство треугольника Презентация по геометрии на тему: Неравенство треугольника 173
Презентация по геометрии: Точка и прямая Презентация по геометрии: Точка и прямая 152
Презентация по геометрии на тему: Сечение многогранников (10 класс) Презентация по геометрии на тему: Сечение многогранников (10 класс) 204
Презентация к уроку 7 Фалес из Милета Презентация к уроку 7 Фалес из Милета 185
Лабораторный практикум по геометрии 7 класс Лабораторный практикум по геометрии 7 класс 152
Найти площадь криволинейной трапеции Найти площадь криволинейной трапеции 129
Чертёж группы геометрических тел Чертёж группы геометрических тел 159
Теорема Пифагора: числа и история Теорема Пифагора: числа и история 148
Решение тригонометрических уравнений способом введения новой переменной Решение тригонометрических уравнений способом введения новой переменной 163
Элементы правильных многогранников Элементы правильных многогранников 169
Задачи на готовых чертежах Задачи на готовых чертежах 182
Формула объема многогранника Формула объема многогранника 369
Параллелепипед 10 класс Параллелепипед 10 класс 183
Построение сечений многогранников Построение сечений многогранников 191
Презентация по геометрии Свойства параллельных прямых Презентация по геометрии Свойства параллельных прямых 141
Презентация по геометрии на тему Площади многоугольников.(8 - 9 классы) Презентация по геометрии на тему Площади многоугольников.(8 - 9 классы) 182
Поверхности и развертки Поверхности и развертки 154
Геометрия и лист бумаги Геометрия и лист бумаги 126
Прямоугольный параллелепипед Прямоугольный параллелепипед 143
Описанная окружность Описанная окружность 188
Презентация по математике ОГЭ. Задания 26. Презентация по математике ОГЭ. Задания 26. 200
Основы планиметрии. Отрезок и прямая. Основы планиметрии. Отрезок и прямая. 140
Презентация к уроку геометрии в 8 классе по теме Четырёхугольники Презентация к уроку геометрии в 8 классе по теме Четырёхугольники 156
Геометрия Лобачевского Геометрия Лобачевского 205
8 класс четырехугольники 8 класс четырехугольники 146
Презентация по теме: Осевая симметрия Презентация по теме: Осевая симметрия 147