- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Правильные многогранники
Содержание
- 2. «Могущественна геометрия; в соединении с искусством –неодолима» Еврипид(древнегреческий драматург )480 – 406 г.г. до н.э.
- 3. 1872 -1970 г Английский математик, философ и общественный
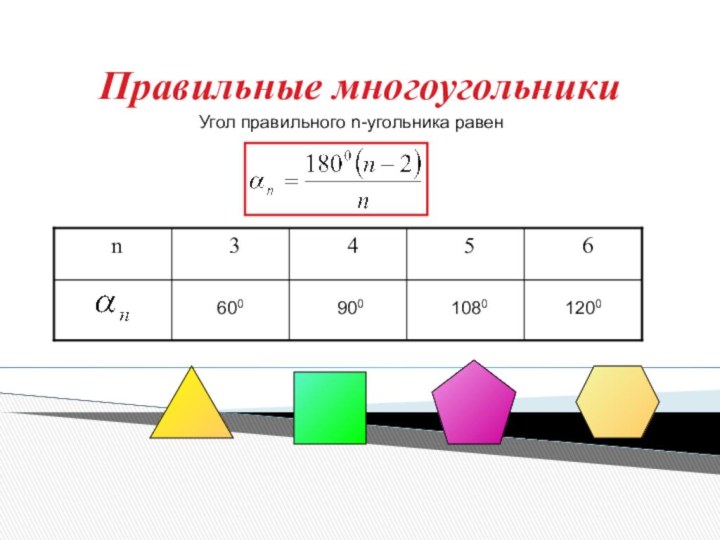
- 4. Правильные многоугольникиУгол правильного n-угольника равен60010801200900
- 5. Грань – правильный треугольник
- 6. Грань – квадратα4 - внутренний угол квадрата.
- 7. Грань – правильный пятиугольник α5 - угол
- 8. Грань – правильный шестиугольник
- 9. Почему правильные многогранники получили такие имена? эдрон
- 10. Определение:Выпуклый многогранник называется правильным,если его гранями являются
- 11. Сделаем вывод: существует лишь пять выпуклых правильных
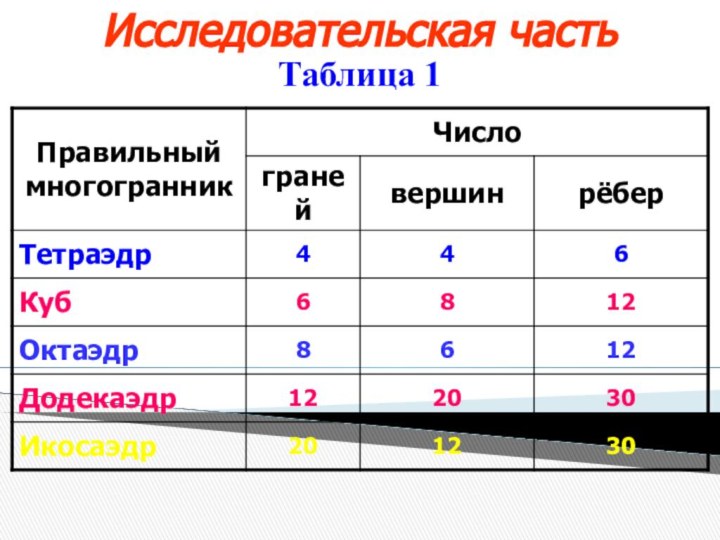
- 12. Правильный тетраэдрCВ переводе с греческого «тетраэдр» -
- 13. Правильный гексаэдрГексаэдр - шестигранник.У правильного гексаэдра (куба)
- 14. Правильный октаэдрОктаэдр - восьмигранник.У октаэдра грани –
- 15. Правильный додекаэдрДодекаэдр - двенадцатигранник.У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
- 16. Правильный икосаэдрИкосаэдр - двадцатигранник.У икосаэдра грани – правильные треугольники. В каждой вершине сходится по пять рёбер.
- 17. Исследовательская частьТаблица 1
- 18. Таблица 2
- 19. Леонард Эйлер(1701-1783)Немецкий математик и физикФормула Эйлера(для правильных многогранников)Г+В=P+2
- 20. Платон428 – 348 г. до н. э.
- 21. Концепция четырех элементовКо времени Платона в античной
- 22. Форма октаэдра – атомы воздуха, ибо воздух
- 23. Большой интерес к формам правильных многогранников проявлялискульпторы,
- 24. ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИГранями полуправильного многогранника являются правильные многоугольники,
- 25. ТЕЛА АРХИМЕДАКроме этих двух бесконечных серий полуправильных
- 26. ТЕЛА АРХИМЕДАЕсли указанным образом срезать вершины октаэдра
- 27. ТЕЛА АРХИМЕДАИз куба и додекаэдра также можно получить усеченный куб и усеченный додекаэдр.
- 28. ТЕЛА АРХИМЕДАДля того чтобы получить еще один
- 29. ТЕЛА АРХИМЕДАЕще два полуправильных многогранника называются усеченный кубооктаэдр и усеченный икосододекаэдр.
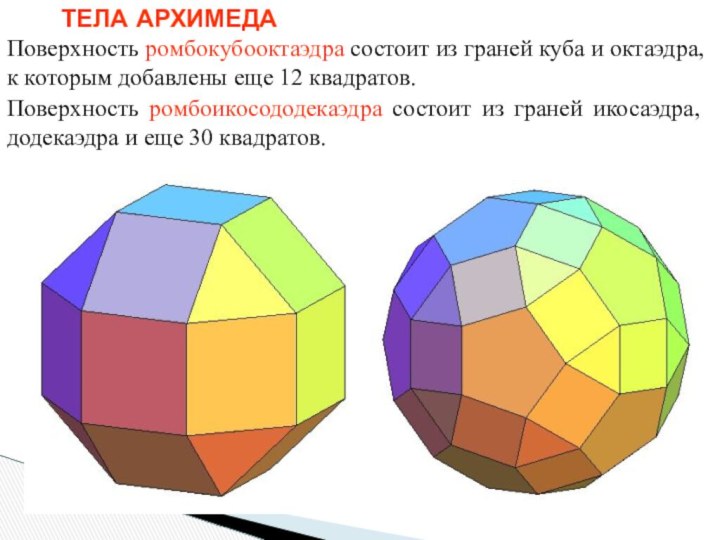
- 30. ТЕЛА АРХИМЕДАПоверхность ромбокубооктаэдра состоит из граней куба
- 31. ТЕЛА АРХИМЕДАПоследние два многогранника – так называемые
- 32. Упражнение 1Укажите номер многогранника, развертка которого изображена на рисунке. Ответ: 1.
- 33. Упражнение 2Укажите номер многогранника, развертка которого изображена на рисунке. Ответ: 3.
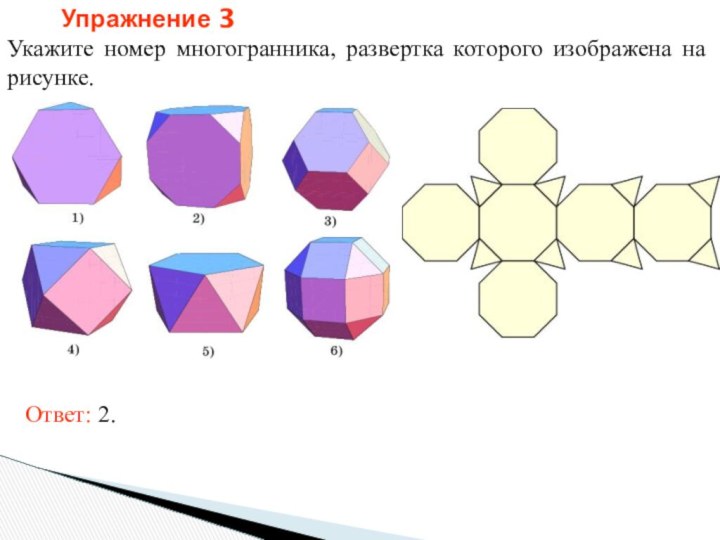
- 34. Упражнение 3Укажите номер многогранника, развертка которого изображена на рисунке. Ответ: 2.
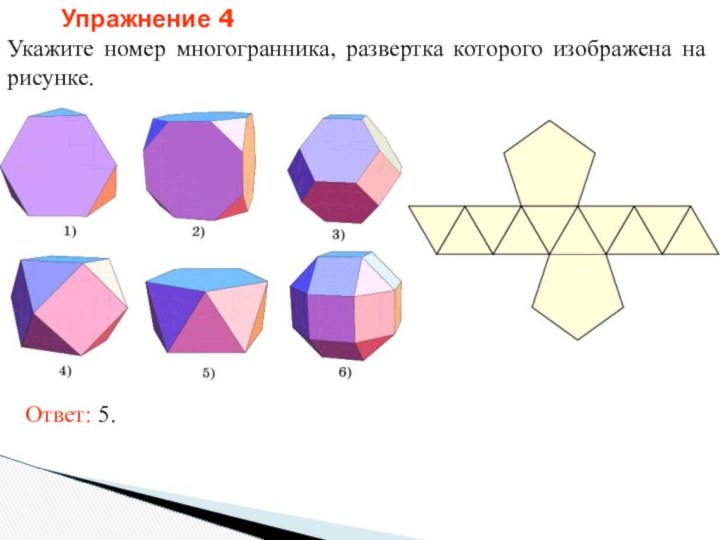
- 35. Упражнение 4Укажите номер многогранника, развертка которого изображена на рисунке. Ответ: 5.
- 36. Форму правильных тел, по-видимому, подсказала древним грекам
- 37. Поваренная соль состоит из кристаллов в форме
- 38. КристаллыПоваренная соль Хрусталь Шеелит Алмаз
- 39. ПРОСТЕЙШЕЕ ЖИВОТНОЕ Скелет одноклеточного организма феодарии по
- 40. ПО ЗАКОНАМ «СТРОГОЙ» АРХИТЕКТУРЫ
- 41. Фаросский маяк
- 42. МНОГОГРАННИКИ В АРХИТЕКТУРЕЧеловек проявляет интерес к многогранникам
- 43. ХРАМ АКРОПОЛЬ В ГРЕЦИИ
- 44. ЦАРСКАЯ ГРОБНИЦА
- 45. МНОГОГРАННИКИ В АРХИТЕКТУРЕ МОСКВЫСобор непорочного зачатия Девы Марии на малой ГрузинскойИсторический музей на Красной площади
- 46. МНОГОГРАННИКИ В КИТАЕ
- 47. Скачать презентацию
- 48. Похожие презентации





































Слайд 2
«Могущественна геометрия;
в соединении с искусством –
неодолима»
Еврипид
(древнегреческий
драматург )
Слайд 3
1872 -1970 г
Английский математик, философ и общественный деятель
Математика владеет не только истиной, но и высшей красотой
– красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел
Слайд 5
Грань – правильный треугольник
α3 – внутренний угол треугольника.
α3 = 60° n – число граней многогранного угла.
1. n = 3 60° · 3 = 180° < 360°
2. n = 4 60° · 4 = 240° < 360°
3. n = 5 60° · 5 = 300° < 360°
4. n = 6 60° · 6 = 360° (многогранный угол совпадает с плоскостью)
Вывод: существует 3 вида правильных многогранников, гранями которых являются правильные треугольники.
Тетраэдр Октаэдр Икосаэдр
Слайд 6
Грань – квадрат
α4 - внутренний угол квадрата.
α4 = 90°
1. n = 3
90° · 3 = 270° < 360° 2. n = 4 90° · 4 = 360° (многогранный,
угол совпадает с плоскостью)
Вывод: существует 1 вид правильных многогранников,
гранями которого являются квадраты.
Куб (гексаэдр)
Слайд 7
Грань – правильный пятиугольник
α5 - угол правильного
пятиугольника
α5 = 108°
1.
n = 3 108° · 3 = 324° < 360°2. n = 4 108° · 4 = 432° > 360°
Вывод: существует 1 вид правильных многогранников, гранями которого являются правильные пятиугольники .
Додекаэдр
Слайд 8
Грань – правильный шестиугольник
α6 = 120°
1. n = 3
120° · 3 = 360° (многогранныйугол совпадает с плоскостью)
Вывод: правильный многогранник,
гранями которого являются правильные шестиугольники не сущесствует.
Слайд 9
Почему правильные многогранники получили такие имена?
эдрон – грань
икоси
- 20
додека - 12
гекса - 6
тетра - 4
окто -
8
Слайд 10
Определение:
Выпуклый многогранник называется правильным,
если его гранями являются правильные
многоугольники
с одним и тем же числом сторон
и в
каждой вершине многогранника сходитсяодно и то же число ребер.
Слайд 11
Сделаем вывод:
существует лишь пять выпуклых правильных
многогранников:
тетраэдр, октаэдр и икосаэдр с треугольными гранями,
куб (гексаэдр)
с квадратными гранями
и додекаэдр
с пятиугольными гранями.
Эти тела называют
телами Платона.
Слайд 12
Правильный тетраэдр
C
В переводе с греческого «тетраэдр» - четырёхгранник
.
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра.
Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
Слайд 13
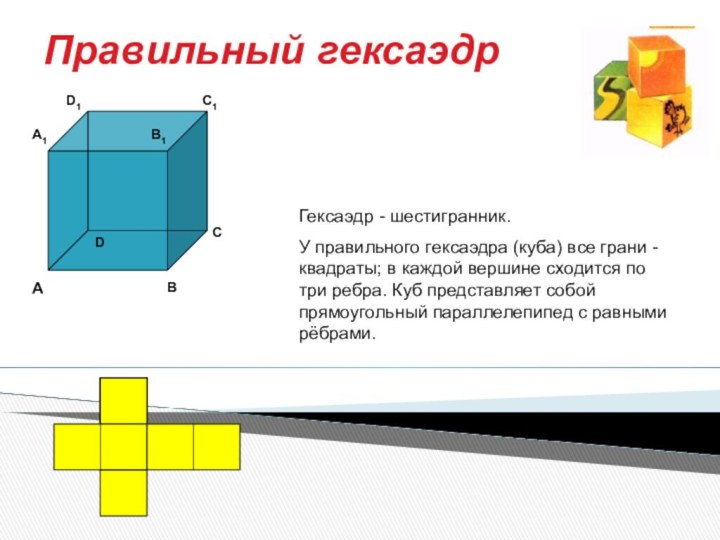
Правильный гексаэдр
Гексаэдр - шестигранник.
У правильного гексаэдра (куба) все
грани -квадраты; в каждой вершине сходится по три ребра.
Куб представляет собой прямоугольный параллелепипед с равными рёбрами.
Слайд 14
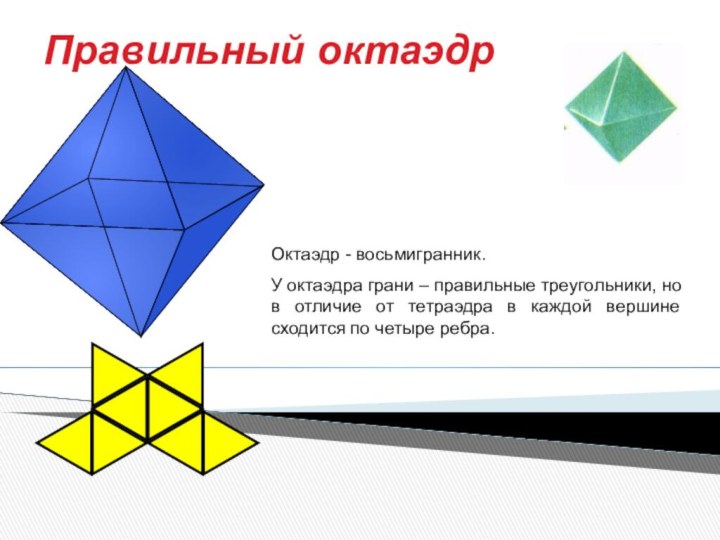
Правильный октаэдр
Октаэдр - восьмигранник.
У октаэдра грани – правильные
треугольники, но в отличие от тетраэдра в каждой вершине
сходится по четыре ребра.
Слайд 15
Правильный додекаэдр
Додекаэдр - двенадцатигранник.
У додекаэдра грани – правильные
пятиугольники. В каждой вершине сходится по три ребра.
Слайд 16
Правильный икосаэдр
Икосаэдр - двадцатигранник.
У икосаэдра грани – правильные
треугольники. В каждой вершине сходится по пять рёбер.
Слайд 19
Леонард Эйлер
(1701-1783)
Немецкий
математик и
физик
Формула Эйлера
(для правильных многогранников)
Г+В=P+2
Слайд 21
Концепция четырех элементов
Ко времени Платона в античной философии
созрела
концепция четырех элементов (стихий) –
первооснов материального мира:
огня, воздуха, воды и земли.
Форма куба – атомы земли, т.к. и земля,
и куб отличаются неподвижностью и устойчивостью.
Форма икосаэдра – атомы воды, т.к. вода отличается
своей текучестью, а из всех правильных тел
икосаэдр – наиболее «катящийся»
Слайд 22
Форма октаэдра – атомы воздуха,
ибо воздух движется
взад и вперед и октаэдр
как бы направлен одновременно
в разные стороныФорма тетраэдра – атомы огня,
т.к. тетраэдр наиболее остр,
кажется, что он мечется в разные стороны.
Платон вводит пятый элемент – «пятую сущность» -
мировой эфир, атомам которого придается форма
додекаэдра как наиболее близкому к шару.
Слайд 23
Большой интерес к формам правильных многогранников проявляли
скульпторы, архитекторы,
художники. Их поражало совершенство,
гармония многогранников. Леонардо да Винчи (1452
– 1519) увлекалсятеорией многогранников и часто изображал их на своих полотнах.
Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со
своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 24
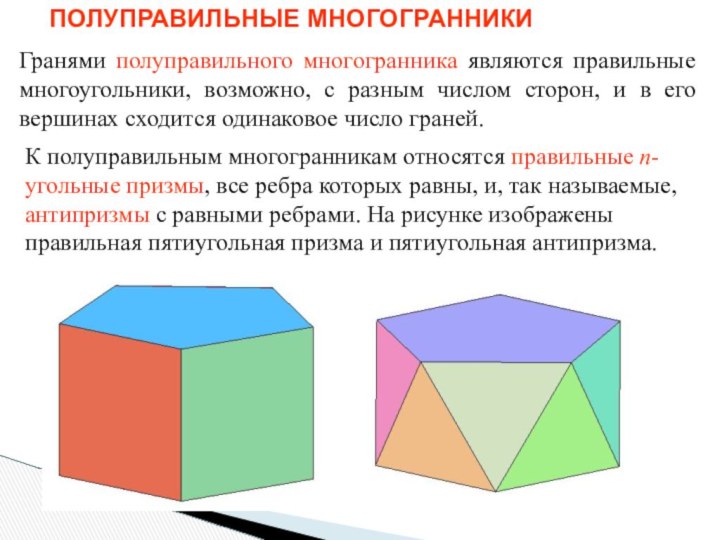
ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Гранями полуправильного многогранника являются правильные многоугольники, возможно,
с разным числом сторон, и в его вершинах сходится
одинаковое число граней.К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны, и, так называемые, антипризмы с равными ребрами. На рисунке изображены правильная пятиугольная призма и пятиугольная антипризма.
Слайд 25
ТЕЛА АРХИМЕДА
Кроме этих двух бесконечных серий полуправильных многогранников,
имеется еще 13 полуправильных многогранников, которые впервые открыл и
описал Архимед - это тела Архимеда.Самые простые из них получаются из правильных многогранников операцией "усечения", состоящей в отсечении плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр.
Слайд 26
ТЕЛА АРХИМЕДА
Если указанным образом срезать вершины октаэдра и
икосаэдра, то получим соответственно усеченный октаэдр и усеченный икосаэдр.
Обратите внимание на то, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра.
Слайд 27
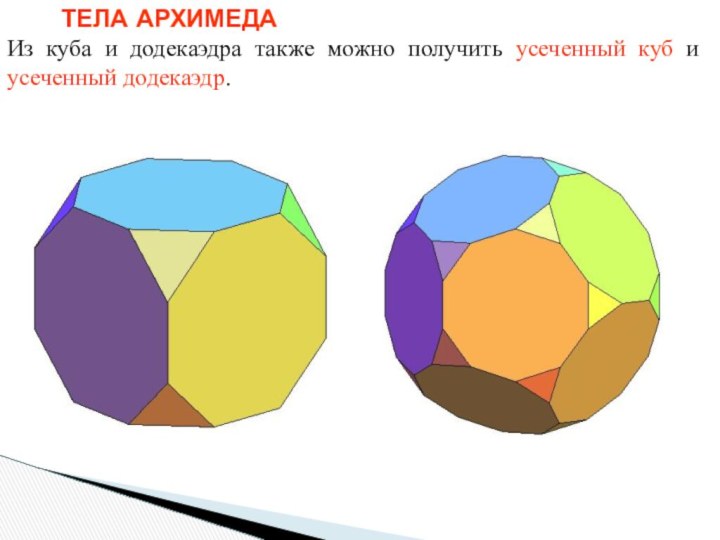
ТЕЛА АРХИМЕДА
Из куба и додекаэдра также можно получить
усеченный куб и усеченный додекаэдр.
Слайд 28
ТЕЛА АРХИМЕДА
Для того чтобы получить еще один полуправильный
многогранник, проведем в кубе отсекающие плоскости через середины ребер,
выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдром. Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром.
Слайд 29
ТЕЛА АРХИМЕДА
Еще два полуправильных многогранника называются усеченный кубооктаэдр
и усеченный икосододекаэдр.
Слайд 30
ТЕЛА АРХИМЕДА
Поверхность ромбокубооктаэдра состоит из граней куба и
октаэдра, к которым добавлены еще 12 квадратов.
Поверхность ромбоикосододекаэдра
состоит из граней икосаэдра, додекаэдра и еще 30 квадратов.
Слайд 31
ТЕЛА АРХИМЕДА
Последние два многогранника – так называемые плосконосый
(иногда называют курносый) куб и плосконосый (курносый) додекаэдр, поверхность
которых состоит из граней куба или додекаэдра, окруженных правильными треугольниками.
Слайд 32
Упражнение 1
Укажите номер многогранника, развертка которого изображена на
рисунке.
Ответ: 1.
Слайд 33
Упражнение 2
Укажите номер многогранника, развертка которого изображена на
рисунке.
Ответ: 3.
Слайд 34
Упражнение 3
Укажите номер многогранника, развертка которого изображена на
рисунке.
Ответ: 2.
Слайд 35
Упражнение 4
Укажите номер многогранника, развертка которого изображена на
рисунке.
Ответ: 5.
Слайд 36 Форму правильных тел, по-видимому, подсказала древним грекам сама
природа:
1) Кристаллы поваренной соли имеют форму куба;
2) Правильная форма
алмаза – октаэдра;3) Кристаллы пирита – додекаэдра.
Слайд 37
Поваренная соль состоит из кристаллов в форме куба
Минерал сильвин также имеет кристаллическую решетку в форме куба.
Молекулы воды имеют форму тетраэдра.
Минерал куприт образует кристаллы в форме октаэдров.
Кристаллы пирита имеют форму додекаэдра
Слайд 39
ПРОСТЕЙШЕЕ ЖИВОТНОЕ
Скелет одноклеточного организма феодарии по форме
напоминает икосаэдр.
Из всех многогранников
с тем же числом граней икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Слайд 40
ПО ЗАКОНАМ «СТРОГОЙ» АРХИТЕКТУРЫ
Пчелиные
соты представляют собой пространственный паркет и заполняют пространство так,
что не остаетсяпросветов.
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»:
«Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».
Слайд 42
МНОГОГРАННИКИ В АРХИТЕКТУРЕ
Человек проявляет интерес к многогранникам на
протяжении всей своей сознательной деятельности – от двухлетнего ребенка,
играющего деревянными кубиками, до зрелого математика. Мы уже знаем, что некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, но мы рассмотрим, какова же цель применение многогранников в архитектуре.
Слайд 43
ХРАМ АКРОПОЛЬ В ГРЕЦИИ
Слайд 44
ЦАРСКАЯ ГРОБНИЦА
История развития многогранников
архитектуре уходит глубоко в историю. Многогранники начали использовать в архитектуре давно, более 7 тыс. лет. Великая пирамида в Гизе - Эта грандиозная Египетская пирамида является древнейшим из семи чудес древности.