- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение сечения куба, нахождение его координат и площади
Содержание
- 2. ЗАДАЧАпо нахождению сечения куба, его координат и площади
- 3. Задача №1 Построить сечение куба, проходящего
- 4. BCDC¹B¹AA¹D¹QPДано:Куб ABCDA¹B¹C¹D¹P – середина BB¹Q –
- 5. Рассмотрим заднюю плоскость BB¹CC¹BB¹CC¹PQA²C²333333BB¹ = B¹C¹ =
- 6. Рассмотрим боковую плоскость DD¹CC¹D = RD¹CC¹C² FDC
- 7. Рассмотрим нижнюю плоскость ABCD ABCEDA²663yРешениеBC = CD
- 8. QPD = RAA¹B¹C¹CD¹BFEA²C²QFREPСечение куба (PQFRE)Сечение куба, проходящей через точки P, Q, R
- 9. QPD = RAA¹B¹C¹CD¹BFEКоординаты точек сечения кубаxyz3333622P (0,
- 10. Нахождение площади сечения кубаQPEFRРазобьём плоскость сечения куба на три треугольника, чтобы подсчитать площадь всего сечения куба.
- 11. S ∆ EPR =Рассмотрим ∆ EPRE (2,
- 12. Рассмотрим ∆ QPRS ∆ QPR =P (0,
- 13. Рассмотрим ∆ FQRF (2, 6, 6 )
- 14. QPEFRНахождение площади сечения куба∆ QPR ++ ∆ QPR+ ∆ FQR+++===
- 15. QFREPСечение куба (PQFRE)P (0, 0, 3)Q (0,
- 16. Задача №2 Построить сечение куба, проходящего
- 17. BCDC¹B¹AA¹D¹QPДано:Куб ABCDA¹B¹C¹D¹P – середина АА¹Q –
- 18. BCDC¹B¹AA¹D¹QP6RКоординаты точек:Р(6;0;3)Q(3;0;6)H(0;3;6)K(0;6;3)F(3;6;0)R(6;3;0)SPQHKFR=HKF
- 19. Задача №3 Построить сечение куба плоскостью,
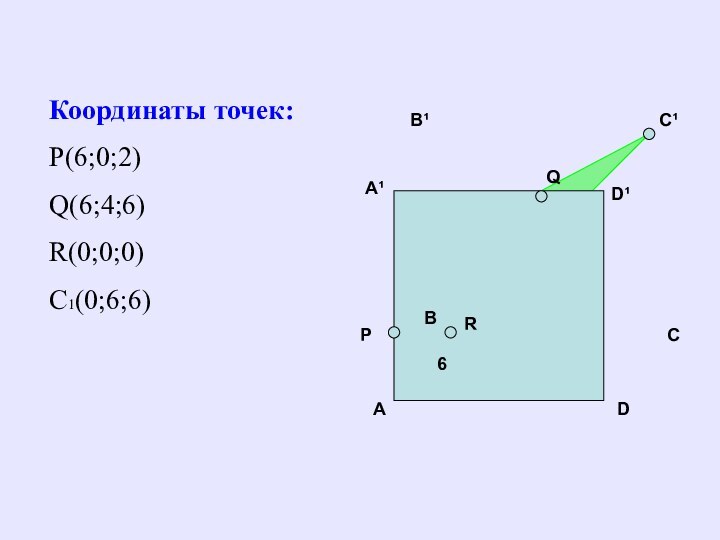
- 20. BCDC¹B¹AA¹D¹QP6RКоординаты точек:Р(6;0;2)Q(6;4;6)R(0;0;0)C1(0;6;6)
- 21. Задача №4 Построить сечение куба плоскостью,
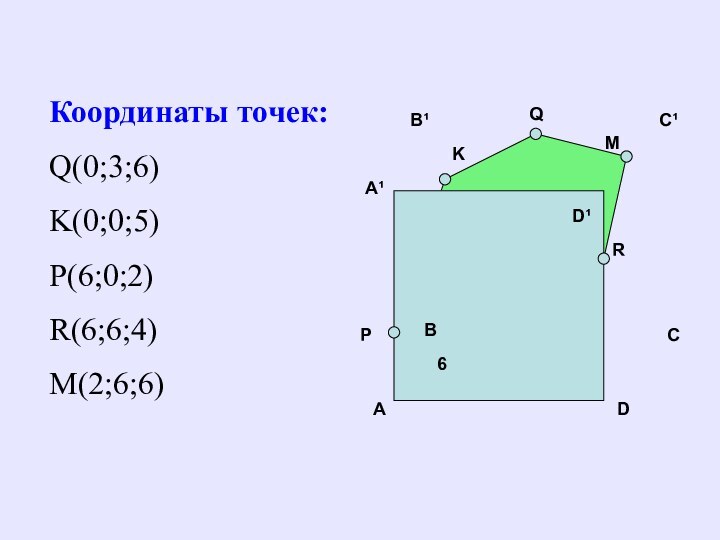
- 22. BCDC¹B¹AA¹D¹QP6RКоординаты точек:Q(0;3;6)K(0;0;5)Р(6;0;2)R(6;6;4)M(2;6;6)KM
- 23. Задача №4 Построить сечение куба плоскостью,
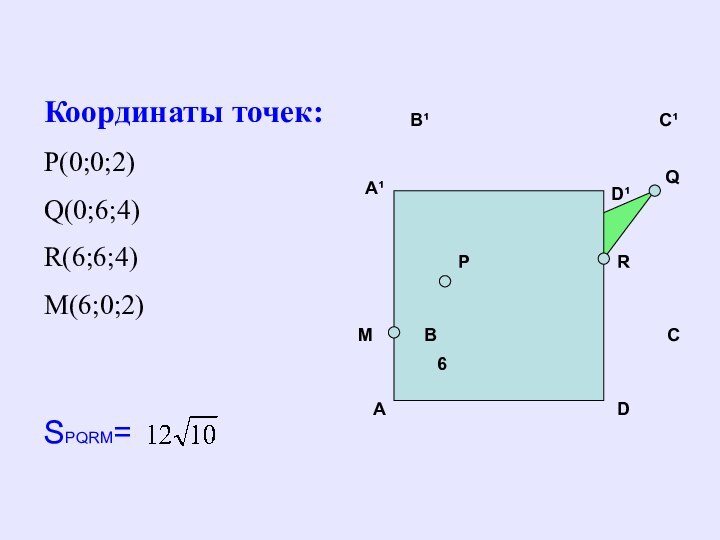
- 24. BCDC¹B¹AA¹D¹QM6RКоординаты точек:Р(0;0;2)Q(0;6;4)R(6;6;4)M(6;0;2)SPQRM=P
- 25. Задачи для самостоятельного решения:Построить сечение куба плоскостью,
- 26. Скачать презентацию
- 27. Похожие презентации
ЗАДАЧАпо нахождению сечения куба, его координат и площади












Слайд 3
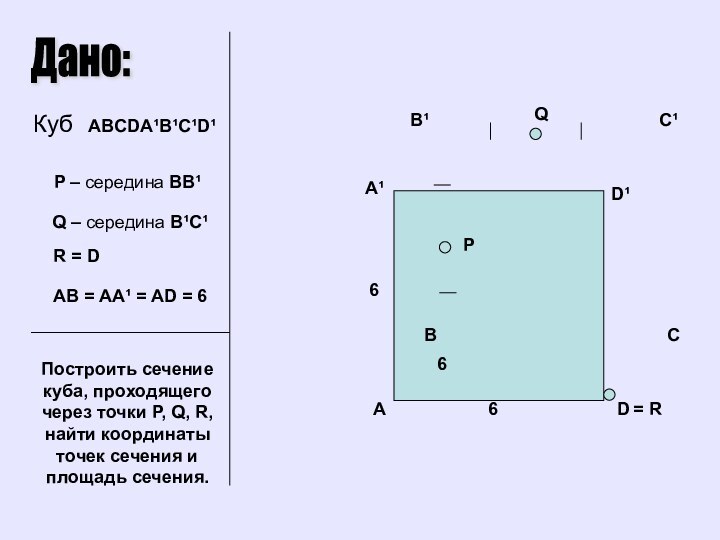
Задача №1
Построить сечение куба, проходящего через
точки P, Q, R, найти координаты точек сечения и
площадь сечения,если P-середина BB1,
Q-середина B1C1,
R=D.
Слайд 4
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
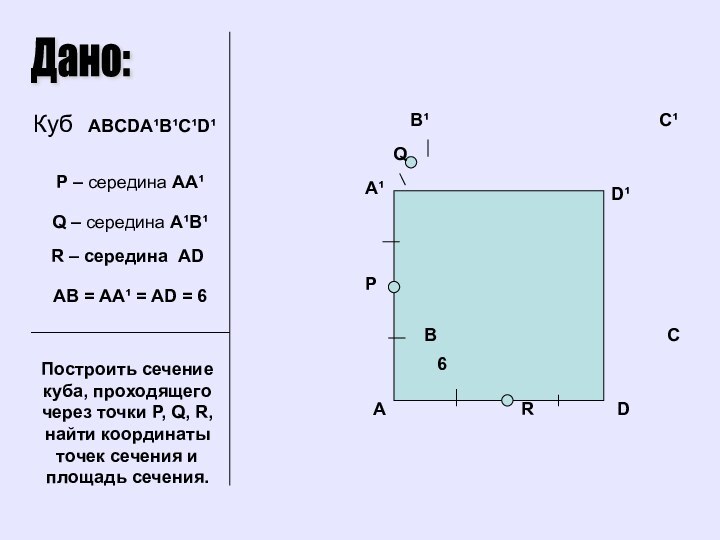
Дано:
Куб ABCDA¹B¹C¹D¹
P – середина BB¹
Q – середина
B¹C¹
R = D
Построить сечение куба, проходящего через точки P,
Q, R, найти координаты точек сечения и площадь сечения.AB = AA¹ = AD = 6
6
6
6
= R
Слайд 5
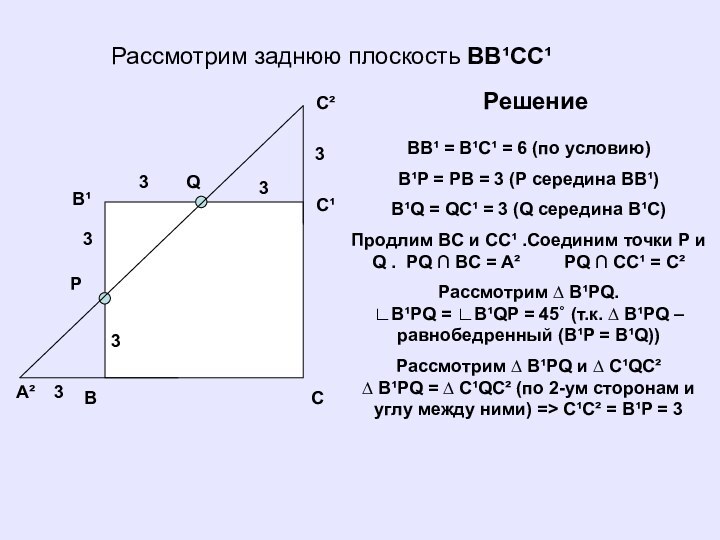
Рассмотрим заднюю плоскость BB¹CC¹
B
B¹
C
C¹
P
Q
A²
C²
3
3
3
3
3
3
BB¹ = B¹C¹ = 6
(по условию)
B¹P = PB = 3 (P середина BB¹)
B¹Q
= QC¹ = 3 (Q середина B¹C) Продлим BC и CC¹ .Соединим точки P и Q . PQ ∩ BC = A² PQ ∩ CC¹ = C²
Рассмотрим ∆ B¹PQ. ∟B¹PQ = ∟B¹QP = 45˚ (т.к. ∆ B¹PQ – равнобедренный (B¹P = B¹Q))
Рассмотрим ∆ B¹PQ и ∆ C¹QC² ∆ B¹PQ = ∆ C¹QC² (по 2-ум сторонам и углу между ними) => C¹C² = B¹P = 3
Решение
Слайд 6
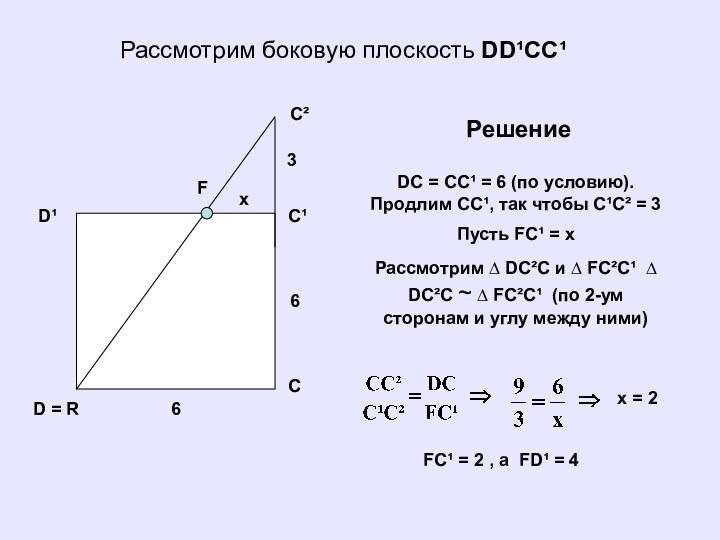
Рассмотрим боковую плоскость DD¹CC¹
D = R
D¹
C
C¹
C²
F
DC =
CC¹ = 6 (по условию). Продлим СC¹, так чтобы
C¹C² = 3Пусть FC¹ = x
Рассмотрим ∆ DC²C и ∆ FC²C¹ ∆ DC²C ~ ∆ FC²C¹ (по 2-ум сторонам и углу между ними)
Решение
3
6
6
x
x = 2
FC¹ = 2 , a FD¹ = 4
Слайд 7
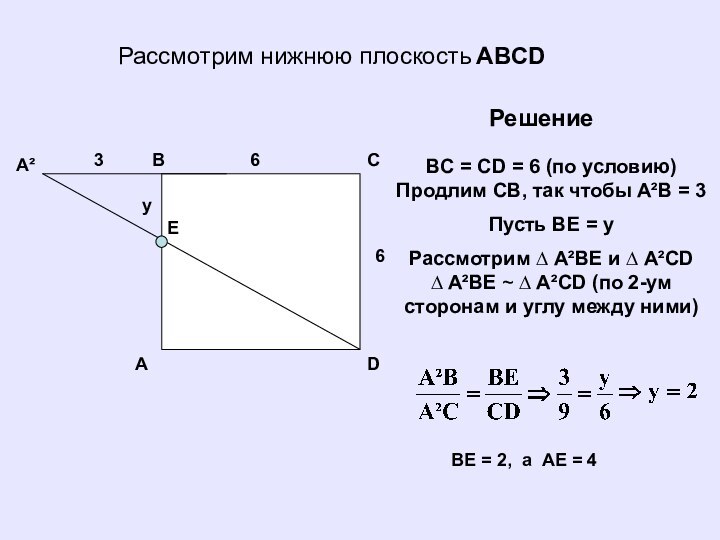
Рассмотрим нижнюю плоскость ABCD
A
B
C
E
D
A²
6
6
3
y
Решение
BC = CD =
6 (по условию) Продлим СB, так чтобы A²B =
3Пусть BE = y
Рассмотрим ∆ A²BE и ∆ A²CD ∆ A²BE ~ ∆ A²CD (по 2-ум сторонам и углу между ними)
BE = 2, а AE = 4
Слайд 8
Q
P
D = R
A
A¹
B¹
C¹
C
D¹
B
F
E
A²
C²
Q
F
R
E
P
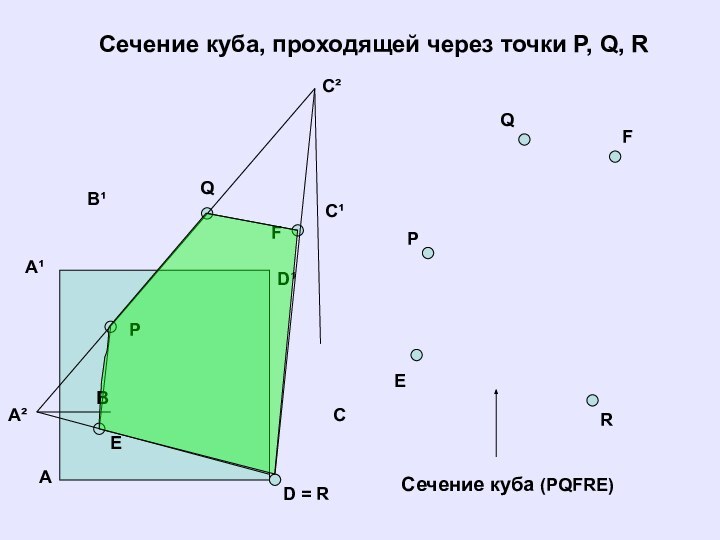
Сечение куба (PQFRE)
Сечение куба, проходящей через
точки P, Q, R
Слайд 9
Q
P
D = R
A
A¹
B¹
C¹
C
D¹
B
F
E
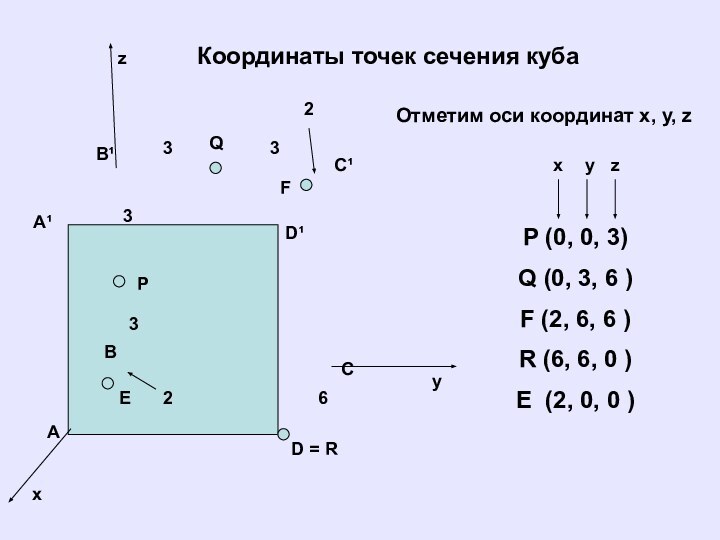
Координаты точек сечения куба
x
y
z
3
3
3
3
6
2
2
P (0, 0,
3)
Q (0, 3, 6 )
F (2, 6, 6 )
R
(6, 6, 0 )E (2, 0, 0 )
x
y
z
Отметим оси координат x, y, z
Слайд 10
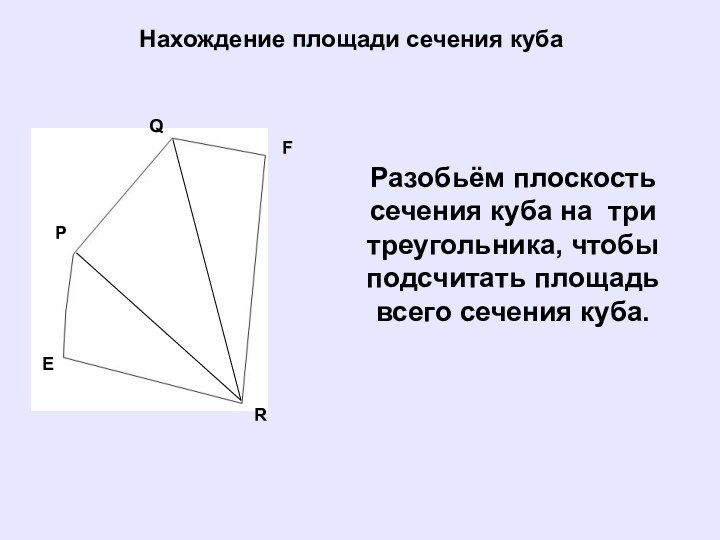
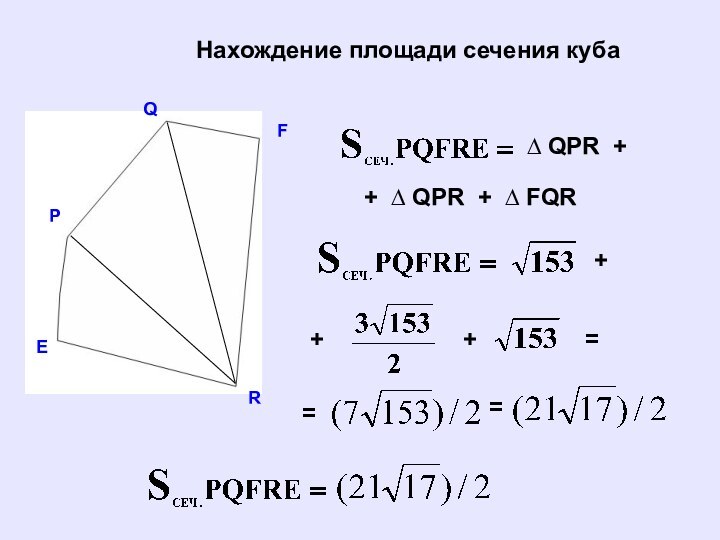
Нахождение площади сечения куба
Q
P
E
F
R
Разобьём плоскость сечения куба на
три треугольника, чтобы подсчитать площадь всего сечения куба.
Слайд 15
Q
F
R
E
P
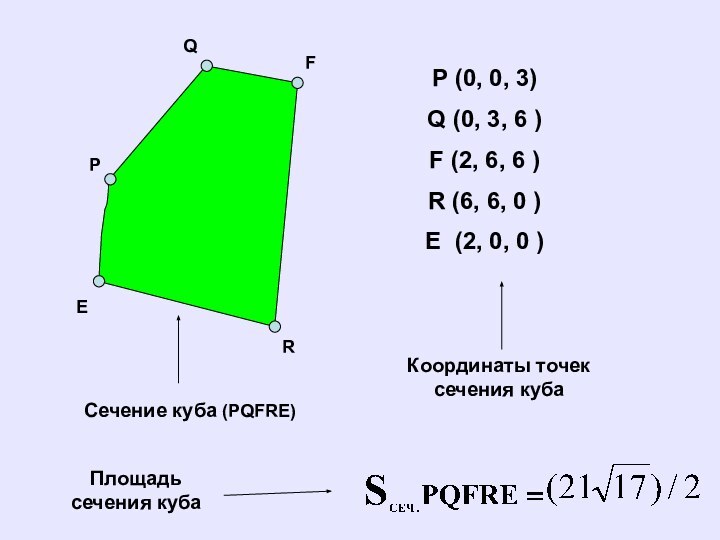
Сечение куба (PQFRE)
P (0, 0, 3)
Q (0, 3,
6 )
F (2, 6, 6 )
R (6, 6, 0
)E (2, 0, 0 )
Координаты точек сечения куба
Площадь сечения куба
Слайд 16
Задача №2
Построить сечение куба, проходящего через
точки P, Q, R, найти координаты точек сечения и
площадь сечения,если P-середина AA1,
Q-середина A1B1,
R- серединаAD.
Слайд 17
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
Дано:
Куб ABCDA¹B¹C¹D¹
P – середина АА¹
Q – середина
А¹В¹
R – середина АD
Построить сечение куба, проходящего через точки
P, Q, R, найти координаты точек сечения и площадь сечения.AB = AA¹ = AD = 6
6
R
Слайд 18
B
C
D
C¹
B¹
A
A¹
D¹
Q
P
6
R
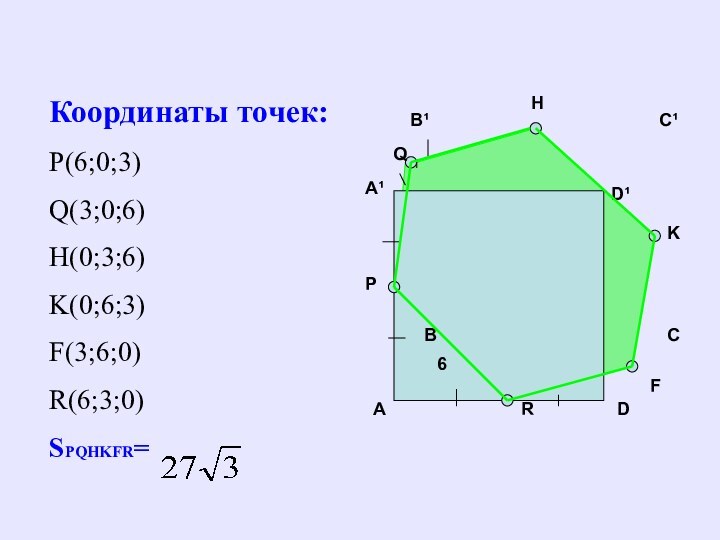
Координаты точек:
Р(6;0;3)
Q(3;0;6)
H(0;3;6)
K(0;6;3)
F(3;6;0)
R(6;3;0)
SPQHKFR=
H
K
F
Слайд 19
Задача №3
Построить сечение куба плоскостью, проходящей
через точки P, Q, R, найти координаты точек сечения,
если P принадлежит AA1,AP=2,
Q принадлежит A1D1,
D1Q=2,
R=B.
Слайд 21
Задача №4
Построить сечение куба плоскостью, проходящей
через точки P, Q, R, найти координаты точек сечения,
если P принадлежит AA1,AP=2,
Q –середина B1C1,
R принадлежит DD1,
D1R=2.
Слайд 23
Задача №4
Построить сечение куба плоскостью, проходящей
через точки P, Q, R, найти координаты точек сечения
и площадь сечения,если P принадлежит BB1,
BP=2,
Q –середина CC1,
C1Q=2,
R принадлежит DD1,
D1R=2.
Слайд 25
Задачи для самостоятельного решения:
Построить сечение куба плоскостью, проходящей
через точки P, Q, R, найти координаты точек сечения
и площадь сечения, если:P принадлежит CC1,C1P=2,
Q- середина AD,R-середина A1B1.
2. P принадлежит CC1,C1P=1,
Q- середина AD,R-середина AA1.