Презентация на тему Вычисление объёма тел

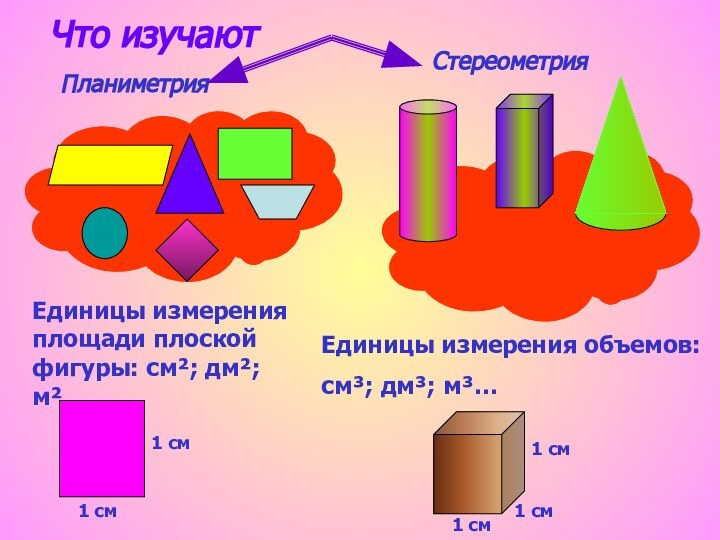
дм²; м²…

1 см
1 см
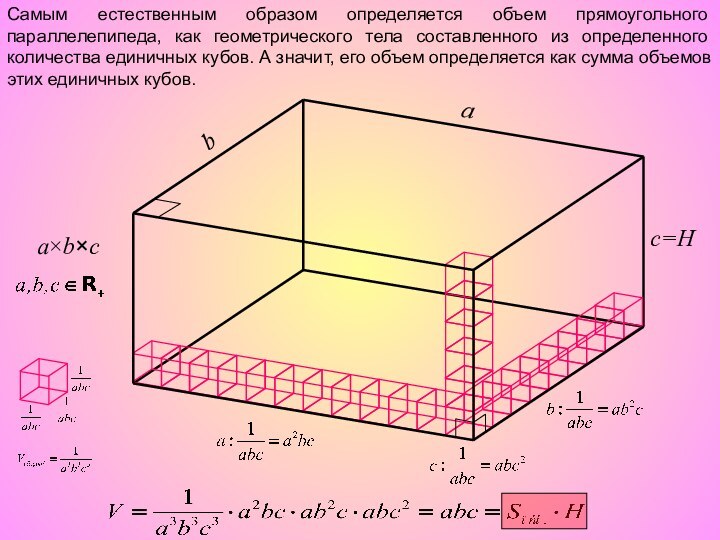
Единицы измерения объемов:
см³; дм³; м³…

1 см
1

см

1 см

Что изучают

объёма;
Узнать формулы объёма прямоугольного параллелепипеда и прямоугольной призмы.

кубы с ребром, равным единице измерения.




















V=20ед.3

В, С имеют равные размеры, то объемы этих тел

– одинаковы.

то объем тела равен объему его частей.



V
V=V1+V2
V1
V2
V

ребро разбивается параллельными плоскостями, проведенными через точки деления ребер

на равные части длиной 1/10 n. объем каждого полученного кубика будет равен 1/10 3n, т.к. длина ребер этого кубика 1/10 n , то
а*10 n; в*10 n; с*10 n
Т.к. n→+∞, то Vn→V=авс
V=a*b*c*10³n* 1/10 3n=a*b*c

геометрического тела составленного из определенного количества единичных кубов. А

значит, его объем определяется как сумма объемов этих единичных кубов.

основания на высоту.
V=Soc*h, т.к. Sос.=a*b;h=c
Следствие 2:
Объем прямой

призмы, основанием которой является прямоугольный треугольник равен произведению площади основания на высоту.
Т.к. ∆ABD-1/2 □АВСД→SABD=½SABCD→VABC=½SABCД*h=
=SABD*h

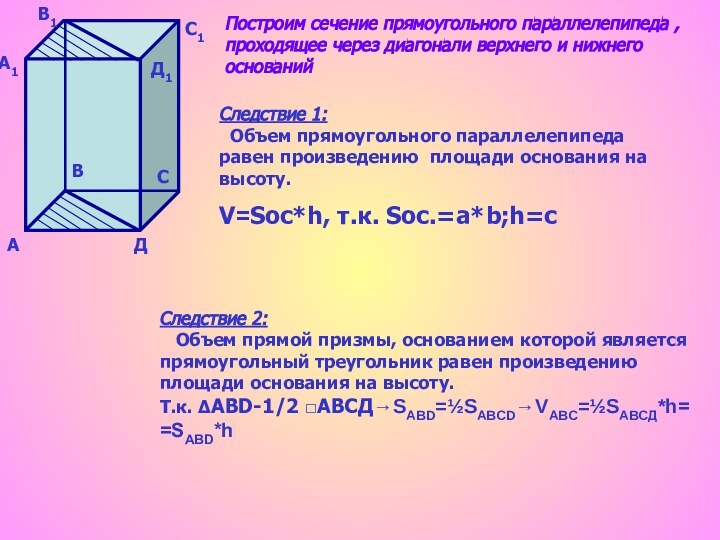
Построим сечение прямоугольного параллелепипеда , проходящее через диагонали верхнего и нижнего оснований

для фигур на плоскости.
Определение 1.  объемом тела называется положительная

величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:
равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;
если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;
за единицу объема принят объем куба, ребро которого равно единице длины;
Определение 2.  Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V1 содержится внутри тела с объемом V2, то V1 < V2.

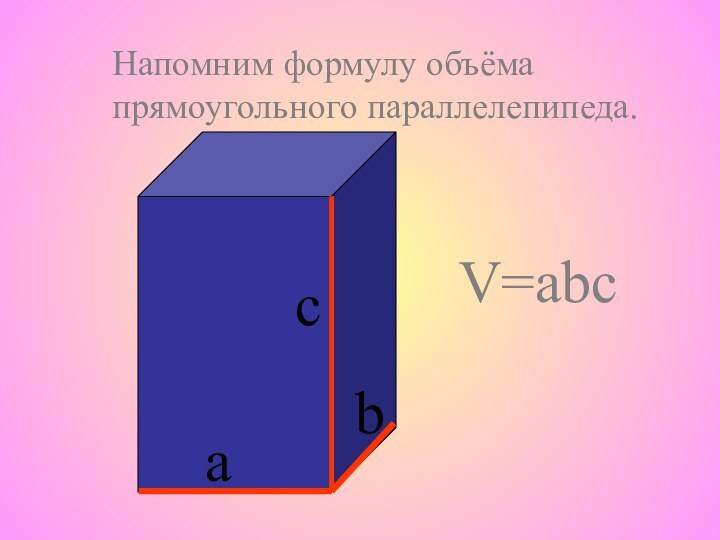
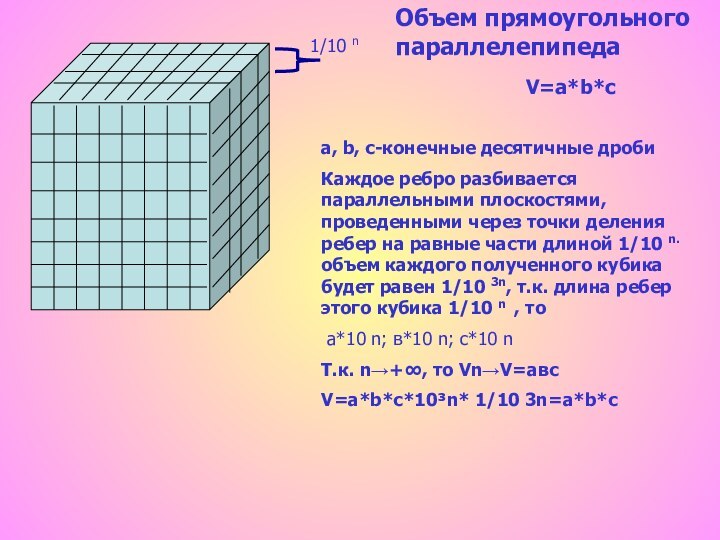
Понятие объема.

Р и Q, имеющих соответственно объемы V1, V2. Выразить

объем V тела R через V1 V2 если б) тела Р и Q имеют общую часть, объем которой равен 1/3V1

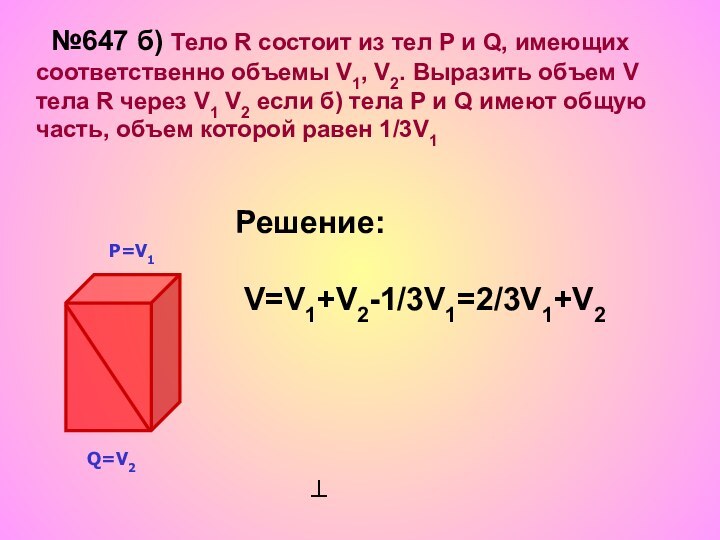
Решение:

V=V1+V2-1/3V1=2/3V1+V2

Р=V1

Q=V2

параллелепипеда, стороны основания которого равны а и b, а

высота равна h, если а=11, b=12, h=15

АС1=3√2
Дано:
АВСДА1В1С1Д1 – куб, АС1=3√2
Найти: V- ?
Решение: Пусть ребро

куба равно а, тогда
из треугольника АДС АС2=а2+а2=2а2,
Рассмотрим треугольник АСС1, найдем АС1

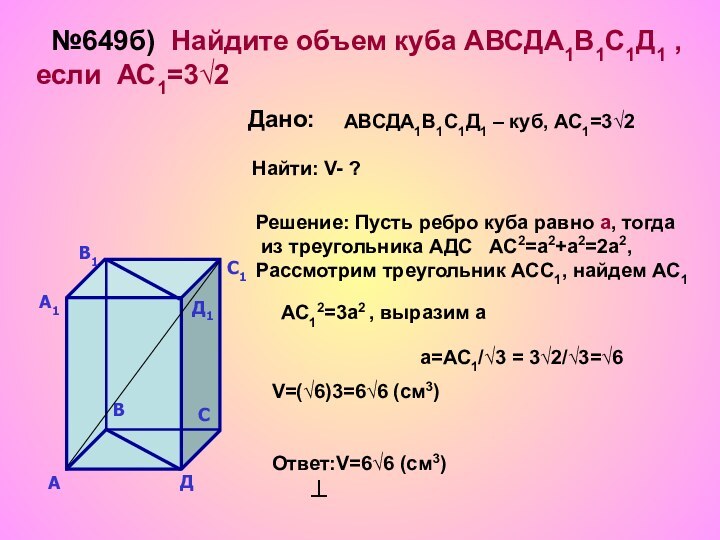
АС12=3а2 , выразим а

а=АС1/√3 = 3√2/√3=√6

V=(√6)3=6√6 (cм3)


Ответ:V=6√6 (см3)

А

А1

В

В1

С

С1

Д

Д1

измерениями 25см, 12см и 6,5см. Плотность кирпича равна 1,8г/cм3.

Найти его массу.

Решение:

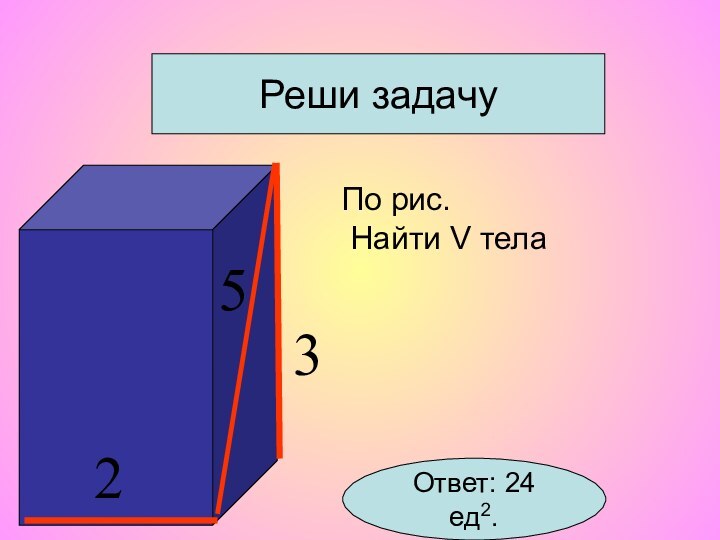
Найдем объем тела
V=25*12*6,5= 1950 (см3)

Связь плотности тела с его массой и объемом
P= m / V m= P*V

m= 1,8*1950=3,51(кг).

Ответ : m =3,51кг.

(по следствию 2)

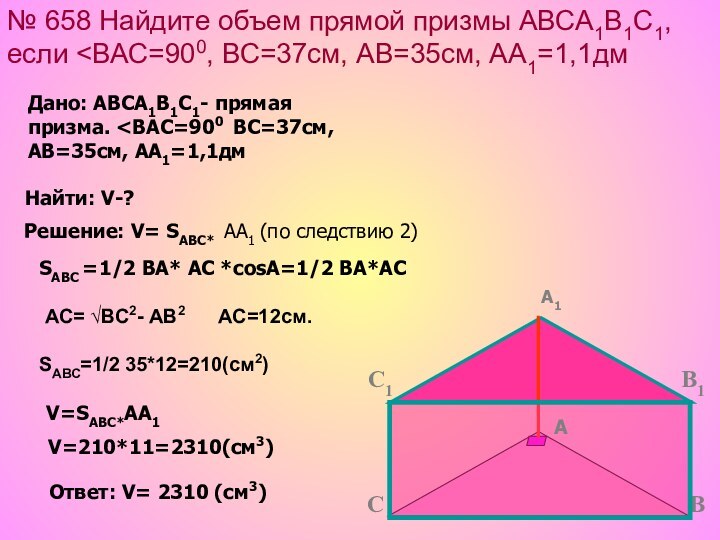
Ответ: V= 2310 (см3)

SАВС =1/2 ВА* АС *cosА=1/2 ВА*АС

АС= √ВС2- АВ2 АС=12см.

SАВС=1/2 35*12=210(см2)

Найти: V-?

Дано: АВСА1В1С1- прямая призма. <ВАС=900 ВС=37см, АВ=35см, АА1=1,1дм

V=SАВС*АА1
V=210*11=2310(см3)

С D B

А1

С1 B1

А

№2
Если тело составлено из нескольких тел, то его объем

равен сумме объемов этих тел.

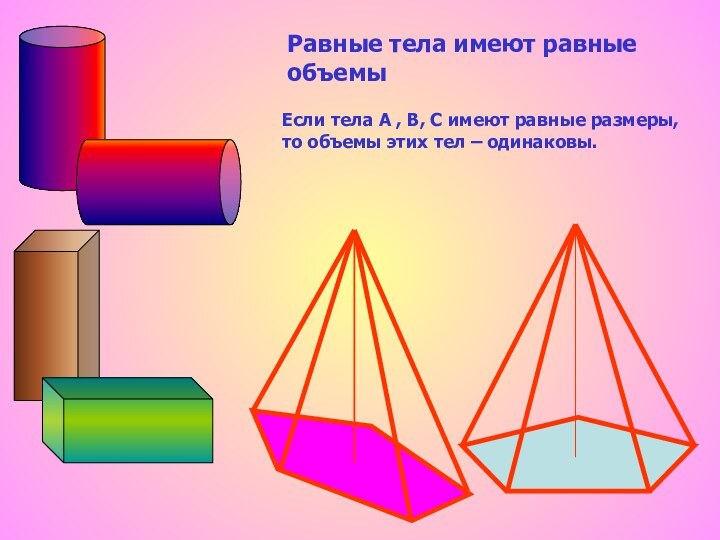
Свойство объемов №3

Если одно тело содержит другое, то объем первого тела не меньше объема второго.

задачу
Ответ: 24 ед2.

5
2
3