Презентация на тему Построение двумерной флаговой геометрии на основе системы аксиом Вейля

и евклидовой геометрии на плоскости
Аксиоматика Вейля флаговой двумерной

геометрии
Свойства векторов флаговой плоскости
Измерение отрезков и углов
Элементы тригонометрии
Движение флаговой плоскости
Принцип двойственности для флаговой плоскости
Заключение
Список используемой литературы

Хуго Вейль (9.XI.1885 - 8.XII.1955). Родился в Эльмсхорне (Германия).

В 1908 г. окончил Геттингенский университет, в том же году защитил диссертацию и получил степень доктора философии. С 1908 до 1913 г. читал лекции в Геттингенском университете в качестве приват-доцента. С 1913 по 1930 г. - профессор Цюрихского политехнического института. В 1930 - 1933 гг. работает в Геттингенском университете, а с 1933 по 1955 г. - в Принстонском институте перспективных исследований (США).
Исследования относятся к теории групп, дифференциальной геометрии, теории интегральных и дифференциальных уравнений, математической логике, основаниям математики, квантовой механике, теории относительности.
Международная премия имени Н.И.Лобачевского присуждена в 1927 году за цикл работ по геометрии и теории линейных представлений групп.

в формировании нашего духовного облика. Занятие математикой – подобно

мифотворчеству, литературе или музыке – это одна из наиболее присущих человеку областей его творческой деятельности, в которой проявляется его человеческая сущность, стремление к интеллектуальной сфере жизни, являющейся одним из проявлений мировой гармонии.
Герман Вейль

Геометрия, которую изучают

в школе, называется евклидовой — по имени геометра, который изложил ее в виде единой логической системы. Великий русский математик Николай Иванович Лобачевский впервые (в 1826 году) обратил внимание на то, что геометрическая система не является чем-либо незыблемым, что ее можно, в случае необходимости, изменить. В результате получится новая геометрическая система, которая ничуть не уступит по своей логической законченности, по научной строгости своего построения, привычной всем нам, евклидовой геометрии. Первую неевклидову геометрию построил Н. И. Лобачевский. После Лобачевского были созданы и многие другие неевклидовы геометрические системы. По сравнению с системой аксиом Д. Гильберта точечно-векторная аксиоматика Г. Вейля (1917) не только позволяет гораздо проще построить евклидову геометрию, но и дает возможность вполне естественным образом построить многие из неевклидовых геометрий.

плоскости
Основными объектами геометрии в аксиоматике

Вейля являются точка и вектор, а основными отношениями — сумма векторов, произведение вектора на число, откладывание вектора от точки, скалярное произведение векторов. Свойства каждого из этих отношений описываются соответствующей группой аксиом. Все аксиомы делятся на пять групп:
I группа. I группа. Аксиомы сложения векторов
II группа. Аксиомы умножения вектора на действительное число
III группа. Аксиомы размерности
IV группа. Аксиомы откладывания вектора от точки
V группа. Аксиомы скалярного произведения
Аксиомы первых трех групп определяют двумерное линейное (или векторное) пространство. Аксиомы первых четырех групп определяют двумерное аффинное пространство. Аксиомами всех пяти групп определяется двумерное евклидово пространство. Таким образом, евклидова геометрия строится на базе аффинной путем введения метрики (меры длины и меры угла) с помощью скалярного произведения векторов. Наоборот, содержание аффинной геометрии можно получить, удаляя из евклидовой геометрии все факты, касающиеся измерения отрезков и углов, в частности перпендикулярность прямых. Важными аффинными понятиями являются параллельность прямых и отношение коллинеарных векторов.

Оставим без изменения все аксиомы Вейля

евклидовой геометрии, кроме аксиомы V5 , которую заменим аксиомой:
V5 *. Существует хотя бы один ненулевой вектор , скалярный квадрат которого равен
нулю ( 2= 0 при ≠ ). Существует хотя бы один вектор , скалярный квадрат которого положителен.
Полученная система аксиом I, II, III, IV, V1-4 , V5 * определяет новую геометрию, называемую флаговой, или полуевклидовой, а также геометрией Галилея. Однако название «геометрия Галилея» исторически неправильно: Галилей не знал этой геометрии, поскольку сама идея существования неевклидовых геометрий возникла гораздо позже и связана с появлением на свет геометрии Лобачевского, а подробная разработка флаговой геометрии относится только к 50-м годам текущего столетия. Название «геометрия Галилея» оправдывается тем, что она связана с принципом относительности Галилея, который гласит: никакие механические эксперименты, производимые внутри физической системы, не могут позволить обнаружить равномерное и прямолинейное движение этой системы.
Название «флаговая геометрия» связано с понятием абсолюта, введением которого заниматься не будем, так как в нашем изложении это понятие не используется.
Сразу подчеркнем, что флаговая геометрия строится на базе аффинной, поэтому все аффинные понятия и теоремы имеют место и во флаговой геометрии (например, теорема о медианах треугольника, теорема о средней линии трапеции и др.).

выяснится в дальнейшем, свойства векторов флаговой плоскости существенно отличаются

от свойств векторов евклидовой плоскости.
Определение. Ненулевые векторы, скалярные квадраты которых равны нулю, называются изотропными векторами.
Теорема 1. Два вектора, один из которых изотропный, а другой неизотропный, линейно независимы. Теорема 1. Два вектора, один из которых изотропный, а другой неизотропный, линейно независимы. Теорема 2. Вектор, коллинеарный изотропному вектору, является изотропными.
Определение. Два вектора называют ортогональными, если их скалярное произведение равно нулю. Ортогональность векторов будем обозначать знаком .
Понятие коллинеарных векторов в смысле флаговой геометрии совпадает с этим понятием в евклидовом (и аффинном) смысле. Однако ортогональные векторы в смысле флаговой геометрии нельзя представлять себе в виде евклидово-ортогональных.
Теорема 3. Ортогональные векторы существуют.
Теорема 4. Два вектора, один из которых изотропный, а другой неизотропный, ортогональны.
Теорема 5. Все изотропные векторы коллинеарны.
Из теорем 2 и 5 вытекает
Следствие. Всякие два изотропных вектора ортогональны.
Теорема 6. Любые два неизотропных ненулевых вектора неортогональны.
На основании теорем 4, 6 и предыдущего следствия имеем
Следствие. Всякому вектору ортогонален изотропный и только изотропный
вектор.

ссылку Вы сможете увидеть содержание данной главы.

измерение отрезков и углов

Рассмотрим аналоги теорем косинусов, синусов и вопрос

о площади треугольника.
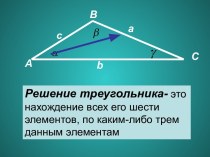
Пусть ABC — треугольник с неизотропными сторонами.
Используя соотношение (5) получаем, что либо с = a – b, либо с = b – a, либо
c = a ± b.
Таким образом, во всяком треугольнике с неизотропными сторонами справедливо одно и только одно их трех соотношений:
a = b + c, b = c + a, c = a + b. (11)
Иначе говоря, во всяком треугольнике с неизотропными сторонами большая сторона равна сумме двух других сторон. Это аналог теоремы косинусов.
Далее, если обозначить, как обычно, через A, В, С величины углов треугольника AВС с неизотропными сторонами а, b, с, то согласно (7) можно получить аналог теоремы синусов (12).
Из соотношений (11) и (12) получаем
Следствие. Во всяком треугольнике с неизотропными сторонами выполняется одно и только одно из трех соотношений:
A = B + C, B = C + A, C = A + B, (13)
т . е. больший угол треугольника равен сумме двух других его углов. Следует учитывать, что меры смежных углов равны. Это непосредственно видно из формулы (8).
Рассмотрим вопрос о площади треугольника. Площадь — понятие аффинное. (Точнее говоря, аффинным понятием является отношение площадей, а площадь — лишь относительный инвариант аффинных преобразова­ний). Поэтому это понятие имеет тот же смысл и во флаговой геометрии.
Пожалуйста, просмотрите эту ссылку
для получения полной информации.

преобразования, сохраняющие длину отрезка и величину угла.
Как

видно из формул (4) и (10), сохранение длин отрезков не влечет за собой обязательного сохранения величины угла. Поэтому в отличие от евклидовой геометрии оба эти требования включены в определение движения.


По этой ссылке перейдите, пожалуйста, на
продолжение этой главы

Во флаговой геометрии имеет место интересный принцип двойственности,

являющийся следствием принципа двойственности для проективной плоскости. можно сформулировать следующий принцип двойственности для флаговой плоскости:
Если истинно некоторое предложение, то будет истинно и другое предложение, которое получается из первого взаимной заменой слов: « точка» — «прямая», «лежит на» — «проходит через», «точки изотропной прямой»—-«параллельные неизотропные прямые», «отрезок» — «угол», «длина отрезка» — «величина угла».
В евклидовой геометрии такой или подобный принцип двойственности не имеет места.
Формулы (11) и (13) взаимно двойственны по этому принципу. Формула (12) двойственна сама себе. Основное достоинство принципа двойственности состоит в том, что он позволяет получать новые теоремы из известных ранее. Для примера рассмотрим теорему, двойственную теореме о медианах треугольника. Легко сообразить, что по принципу двойственности серединам сторон треугольника соответствуют биссектрисы (конечно, в смысле флаговой геометрии) углов треугольника, поэтому прямым, содержащим медианы, соответствуют точки пересечения биссектрис с противоположными им сторонами, а медианам соответствуют углы между биссектрисами и этими сторонами. Таким образом, теорема о медианах треугольника по принципу двойственности переходит в новую теорему:
Точки пересечения биссектрис (неравнобедренного) треугольника с противоположными им сторонами лежат на одной прямой, которая делит углы, образованные биссектрисами с противоположными сторонами треугольника, в отношении 2:1, считая от стороны.

Глава полностью

Мы видим, что флаговая геометрия много проще евклидовой. Это

ценно в том отношении, что при сравнительно небольшой затрате сил и времени на примере построения этой геометрии можно дать конкретное представление о принципах евклидовых геометрий. Изобретение неевклидовой геометрии имело большое философское значение: оно показало, что ошибочен взгляд философов-идеалистов, считавших, что существуют истины, которые присущи нашему сознанию до всякого опыта, и приводивших в качестве примеров таких истин аксиомы евклидовой геометрии. Создание неевклидовой геометрии оказало большое влияние на развитие физики. Неевклидовы геометрии оказались полезным аппаратом при создании новых важных физических теорий, среди которых в первую очередь следует назвать общую теорию относительности А. Эйнштейна.