- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
- 2. Что такое правильный многогранник?Правильный многогранник - многогранник,
- 3. ОпределениеМногогранник называется правильным, если:он выпуклый;все его грани
- 4. Виды правильных многогранниковСуществует всего пять видов правильных многогранников:ТетраэдрОктаэдрИкосаэдрГексаэдр или куб Додекаэдр
- 5. ТетраэдрТетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший
- 6. ОктаэдрОкта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь»
- 7. ИкосаэдрИкоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение»,
- 8. ГексаэдрКуб или правильный гексаэдр — правильный многогранник,
- 9. ДодекаэдрДодека́эдр (от греч. δώδεκα — двенадцать и
- 10. Платоновы телаПравильные многогранники иногда называют Платоновыми телами,
- 11. Многогранники вокруг насПравильные многогранники – самые выгодные
- 12. Правильные многогранники в химииПри производстве алюминия пользуются
- 13. Скачать презентацию
- 14. Похожие презентации
Что такое правильный многогранник?Правильный многогранник - многогранник, все грани которого - одинаковые правильные многоугольники и все многогранные углы при вершинах равны между собой.









![Правильные многогранники Правильные многогранники в химииПри производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] × 12H2O),](/img/tmb/12/1140219/d21e4597b3d66187a6e1186e7a223fe7-720x.jpg)

Слайд 3
Определение
Многогранник называется правильным, если:
он выпуклый;
все его грани являются
равными правильными многоугольниками;
в каждой его вершине сходится одинаковое число
рёбер.
Слайд 4
Виды правильных многогранников
Существует всего пять видов правильных многогранников:
Тетраэдр
Октаэдр
Икосаэдр
Гексаэдр
или куб
Додекаэдр
Слайд 5
Тетраэдр
Тетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший многогранник,
гранями которого являются четыре треугольника. У тетраэдра 4 грани,
4 вершины и 6 рёбер.
Слайд 6
Октаэдр
Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и
греч. έδρα — «основание») — один из пяти выпуклых
правильных многогранников, так называемых Платоновых тел.Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Слайд 7
Икосаэдр
Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение», «основание»)
— правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Слайд 8
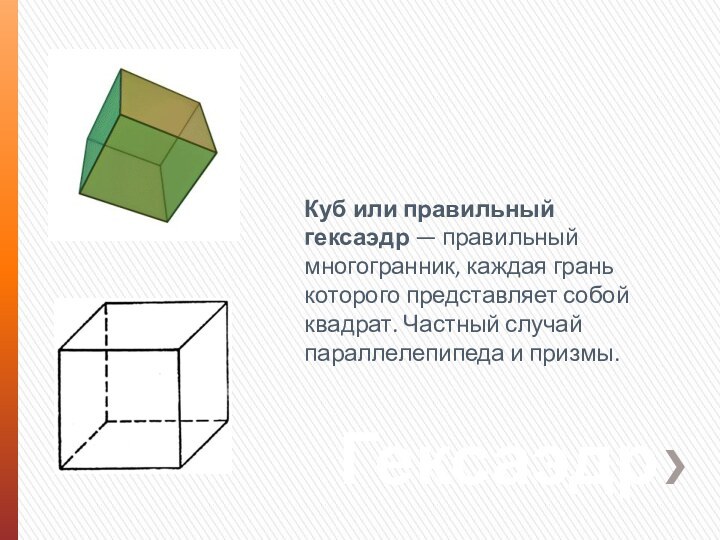
Гексаэдр
Куб или правильный гексаэдр — правильный многогранник, каждая
грань которого представляет собой квадрат. Частный случай параллелепипеда и
призмы.
Слайд 9
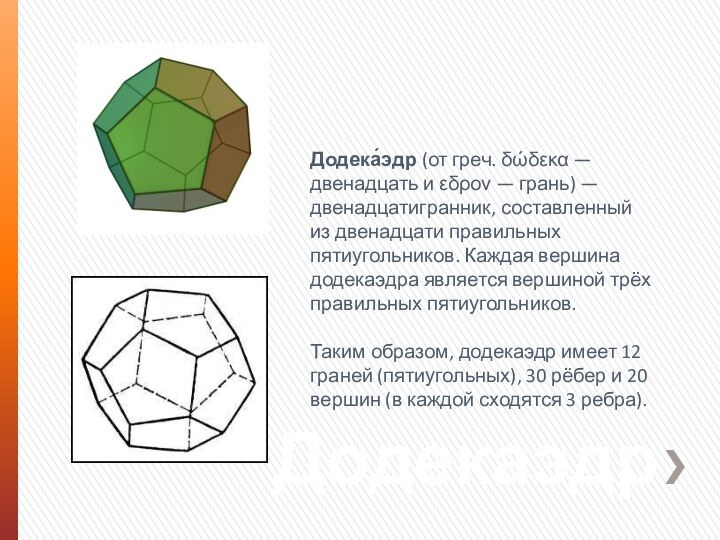
Додекаэдр
Додека́эдр (от греч. δώδεκα — двенадцать и εδρον
— грань) — двенадцатигранник, составленный из двенадцати правильных пятиугольников.
Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).