- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площади фигур
Содержание
- 2. Работу выполняла ученица 11«4» класса Степанова Аня
- 3. Основные свойства площадей.
- 4. Первое свойство:Площадь плоской фигуры – неотрицательное число.АСВ
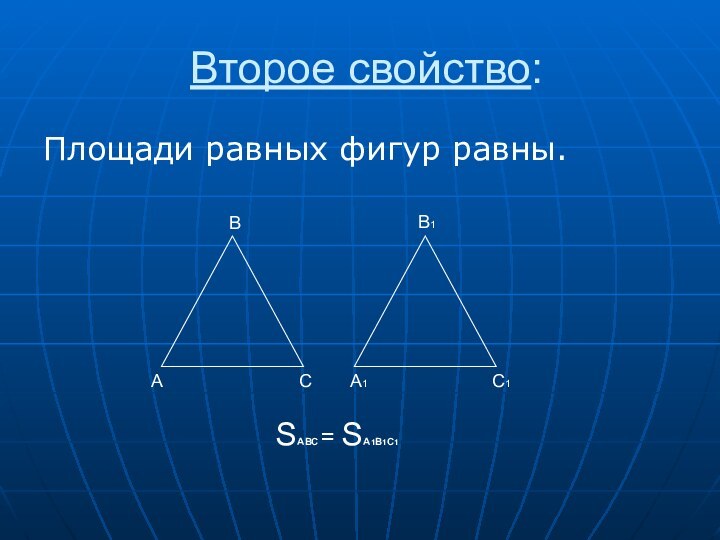
- 5. Второе свойство:Площади равных фигур равны.АВСА1С1В1SАВС = SА1В1С1
- 6. Третье свойство:Если фигура разрезана на несколько частей, то ее площадь равна сумме площадей этих частей.
- 7. Четвертое свойство:Площадь квадрата со стороной 1 равна 1. АВСDааSАВСD =a²а=1
- 8. Разрезания и складывания Основной принцип метода "разрезания
- 9. ТеоремаЕсли два многоугольника равновелики, то один из
- 10. Отношения площадей для того, чтобы установить связь
- 11. Площадь многоугольникаЕсли многоугольник составлен из нескольких многоугольников,
- 12. Площадь квадратаРассмотрев 4 свойство, докажем, что площадь
- 13. ЗадачаПусть O – точка пересечения отрезков АС
- 14. Решение: Для того, чтобы решить эту
- 15. Площадь прямоугольника. Теорема: Площадь прямоугольника равна произведению его смежных сторон.
- 16. Доказательство теоремы:Достроим прямоугольник до квадрата со стороной
- 17. решение C другой стороны, этот квадрат составлен
- 18. Площадь параллелограмма. Теорема: Площадь параллелограмма равна произведению его основания на высоту.
- 19. Доказательство: Рассмотрим параллелограмм ABCD с площадью S.
- 20. Докажем сначала, что площадь прямоугольника НВСК
- 21. Площадь треугольника. Теорема:Площадь треугольника равна половине произведения его основания на высоту.S=½АВ ∙ СН
- 22. Доказательство: Пусть S – площадь треугольника АВС.
- 23. Следствие 1: Площадь прямоугольного треугольника равна половине произведения его катетов.
- 24. Следствие 2: Если высоты двух треугольников
- 25. Теорема: Если угол одного треугольника равен углу
- 26. Доказательство: Пусть S и S1 – площади
- 27. Наложим треугольники АВС на треугольник А1В1С1
- 28. Площадь трапеции.Для вычисления площади произвольного многоугольника обычно
- 29. Теорема:Площадь трапеции равна произведению полу-суммы ее оснований на высоту.
- 30. Скачать презентацию
- 31. Похожие презентации
Работу выполняла ученица 11«4» класса Степанова Аня





















Слайд 6
Третье свойство:
Если фигура разрезана на несколько частей, то
ее площадь равна сумме площадей этих частей.
Слайд 8
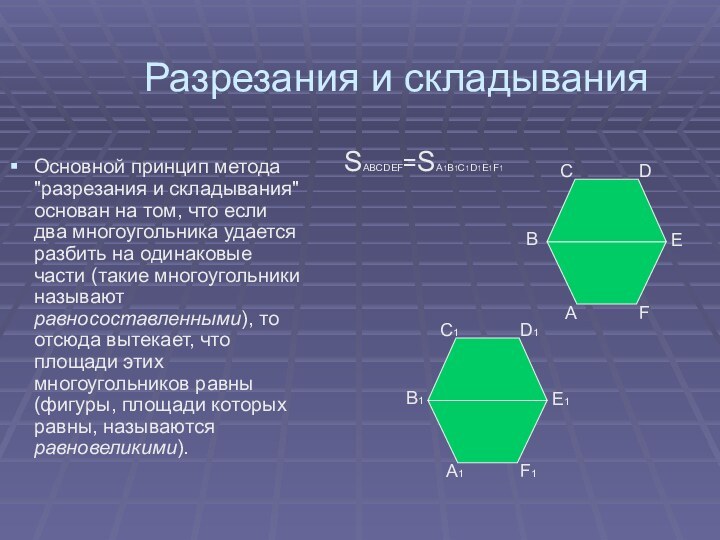
Разрезания и складывания
Основной принцип метода "разрезания и
складывания" основан на том, что если два многоугольника удается
разбить на одинаковые части (такие многоугольники называют равносоставленными), то отсюда вытекает, что площади этих многоугольников равны (фигуры, площади которых равны, называются равновеликими).А
В
С
D
Е
F
А1
В1
С1
D1
Е1
F1
SABCDEF=SA1B1C1D1E1F1
Слайд 9
Теорема
Если два многоугольника равновелики, то один из них
можно разрезать на части, из которых можно составить другой
многоугольник.
Слайд 10
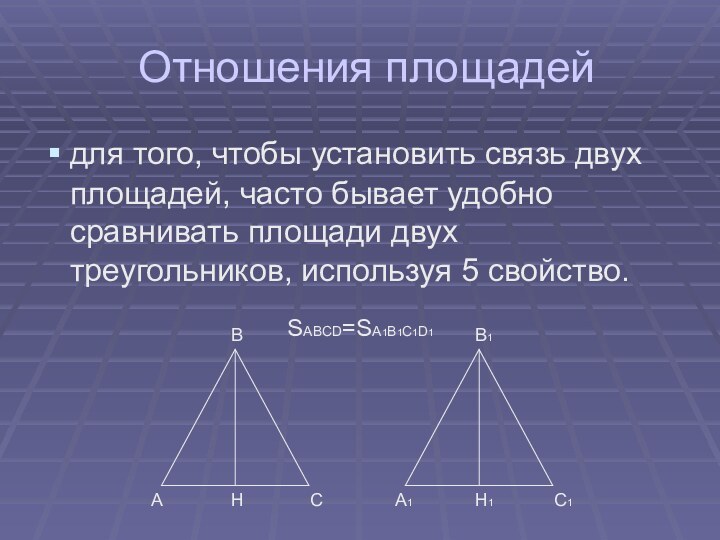
Отношения площадей
для того, чтобы установить связь двух
площадей, часто бывает удобно сравнивать площади двух треугольников, используя
5 свойство.А
С
В
Н
А1
С1
В1
Н1
SABCD=SA1B1C1D1
Слайд 11
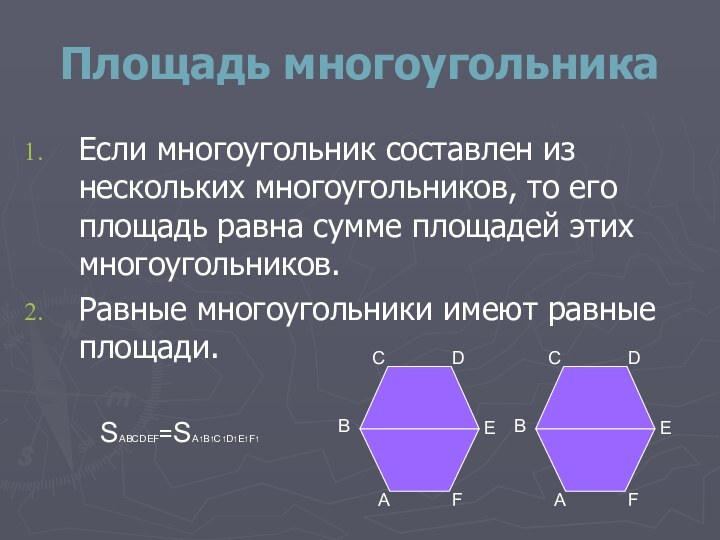
Площадь многоугольника
Если многоугольник составлен из нескольких многоугольников, то
его площадь равна сумме площадей этих многоугольников.
Равные многоугольники имеют
равные площади.А
В
С
D
Е
F
А
В
С
D
Е
F
SABCDEF=SA1B1C1D1E1F1
Слайд 12
Площадь квадрата
Рассмотрев 4 свойство, докажем, что площадь S
квадрата со стороной а равна а².
Начнем с того случая,
когда а=1/n.Где n-целое число. Возьмем квадрат со стороной 1 и разобьем его на n² равных квадратов. Так как площадь большого квадрата равна 1 То площадь каждого маленького квадрата равна 1/n²1/n
1
Слайд 13
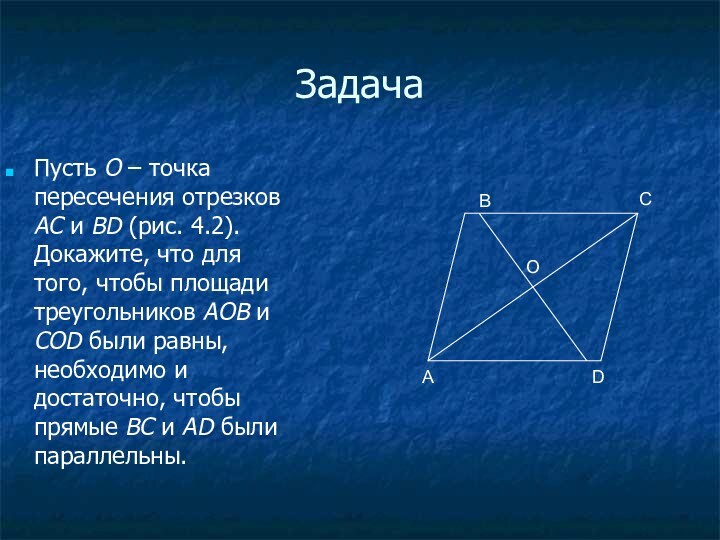
Задача
Пусть O – точка пересечения отрезков АС и
BD (рис. 4.2). Докажите, что для того, чтобы площади
треугольников AOB и COD были равны, необходимо и достаточно, чтобы прямые ВС и AD были параллельны.А
В
С
D
O
Слайд 14
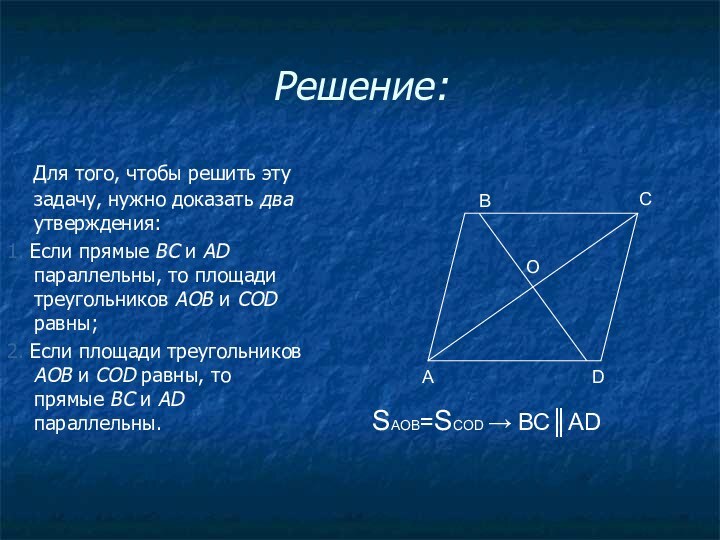
Решение:
Для того, чтобы решить эту
задачу, нужно доказать два утверждения:
1. Если прямые ВС и
AD параллельны, то площади треугольников АОВ и COD равны; 2. Если площади треугольников АОВ и COD равны, то прямые ВС и AD параллельны.
А
В
С
D
O
SАОВ=SСОD → ВС║АD
Слайд 15
Площадь прямоугольника. Теорема:
Площадь прямоугольника равна произведению его
смежных сторон.
Слайд 16
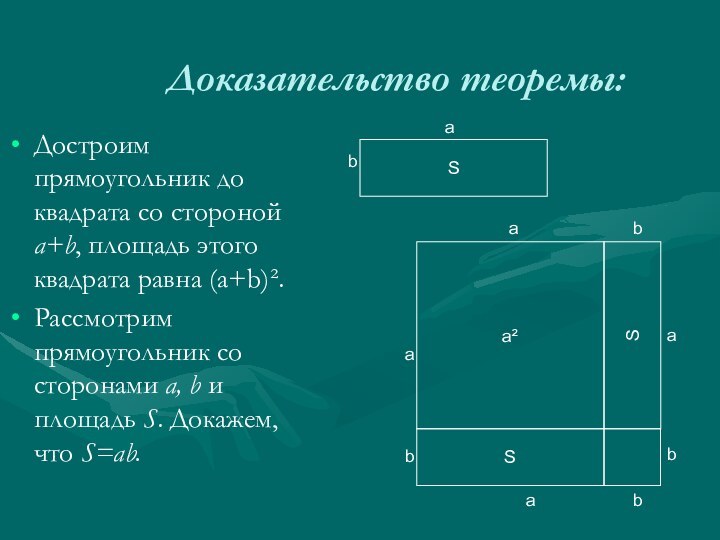
Доказательство теоремы:
Достроим прямоугольник до квадрата со стороной а+b,
площадь этого квадрата равна (а+b)².
Рассмотрим прямоугольник со сторонами а,
b и площадь S. Докажем, что S=аb.S
S
S
а²
а
b
a
b
b
а
а
b
b
a
Слайд 17
решение
C другой стороны, этот квадрат составлен из
данного прямоугольника с площадью S, равного ему прямоугольника с
площадью S и двух квадратов с площадями а² и b². Имеем: (a+b)²=S+S+a²+b²От сюда получаем S=ab.
Теорема доказана.
Слайд 18
Площадь параллелограмма.
Теорема:
Площадь параллелограмма равна произведению его
основания на высоту.
Слайд 19
Доказательство:
Рассмотрим параллелограмм ABCD с площадью S. Примем
сторону AD за основание и проведем высоту ВН и
СК. Требуется доказать, чтоS=AD∙BH
А
Н
D
K
C
B
1
2
Слайд 20 Докажем сначала, что площадь прямоугольника НВСК также
равна S. Трапеция АВСК составлена из параллелограмма АВСD и
треугольника DCK. С другой стороны, она составлена из прямоугольников НВСК и треугольник АВН. Но прямоугольные треугольники DCK и АВН равны по гипотенузе и остр. углу (АВ=СD, углы 1=2),поэтому их площади равны. Следовательно, площади параллелограмма АВСD и прямоугольника НВСК также равны, т. е. площадь прямоугольника НВСК равна S. По теореме о площади прямоугольника S=BC∙BH, а так как ВС=АD, то S=AD∙BH. Теорема доказана.
Слайд 21
Площадь треугольника.
Теорема:
Площадь треугольника равна половине произведения его
основания на высоту.
S=½АВ ∙ СН
Слайд 22
Доказательство:
Пусть S – площадь треугольника АВС. Примем
сторону АВ за основание и проведем высоту СН. Докажем,
чтоS=½АВ∙СН
Достроим треугольник АВС до параллелограмма АВDС.Треугольники АВС и DСВ равны по трем сторонам (ВС - их общая сторона, АВ=СD и АС=ВD), поэтому их площади равны. Следовательно, площадь S треугольника АВС равны половине площади параллелограмма АВDС, т. Е. S=½АВ∙СН. Теорема доказана.
А
Н
D
C
B
Слайд 24
Следствие 2:
Если высоты двух треугольников равны
,то их площади относятся как основания.
Воспользовавшись этим
следствием докажем теорему об отношении площадей треугольников, имеющих по равному углу.
Слайд 25
Теорема:
Если угол одного треугольника равен углу другого
треугольника, то площади этих треугольников относятся как произведения сторон,
заключающих равные углы.
Слайд 26
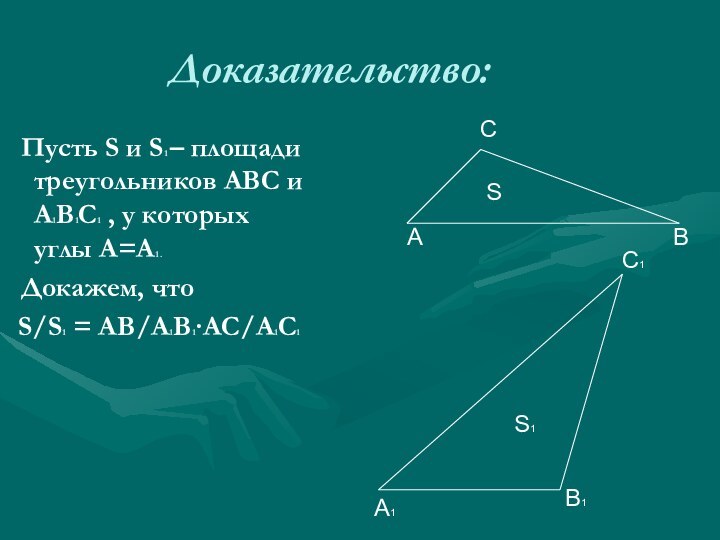
Доказательство:
Пусть S и S1 – площади треугольников
АВС и А1В1С1 , у которых углы А=А1 .
Докажем, что S/S1 = АВ/А1В1∙АС/А1С1
С
В
А
S
А1
С1
В1
S1
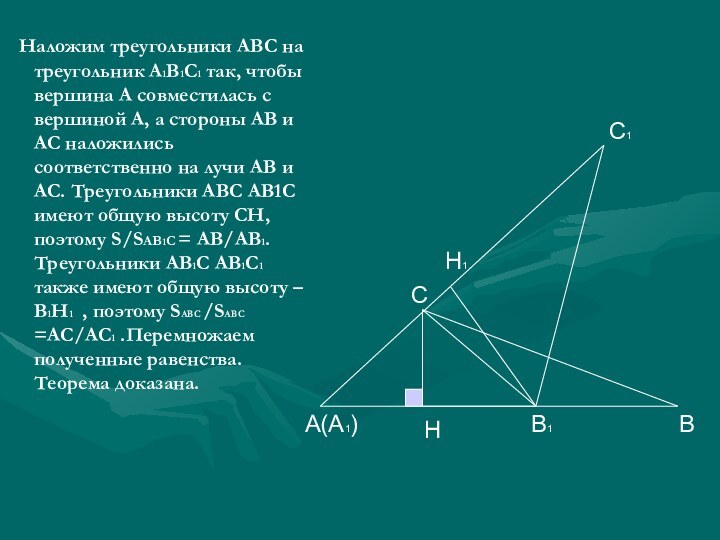
Слайд 27 Наложим треугольники АВС на треугольник А1В1С1 так,
чтобы вершина А совместилась с вершиной А, а стороны
АВ и АС наложились соответственно на лучи АВ и АС. Треугольники АВС АВ1С имеют общую высоту СН, поэтому S/SАВ1С = АВ/АВ1. Треугольники АВ1С АВ1С1 также имеют общую высоту – В1Н1 , поэтому SАВС /SАВС =АС/АС1 .Перемножаем полученные равенства. Теорема доказана.С
А(А1)
Н
В1
В
Н1
С1
Слайд 28
Площадь трапеции.
Для вычисления площади произвольного многоугольника обычно поступают
так: разбивают многоугольник на треугольники и находят площадь каждого
треугольника. Сумма площадей этих треугольников равна площади данного многоугольника.S3
S2
S1
S=S1+S2+S3