Презентация на тему Понятие движения

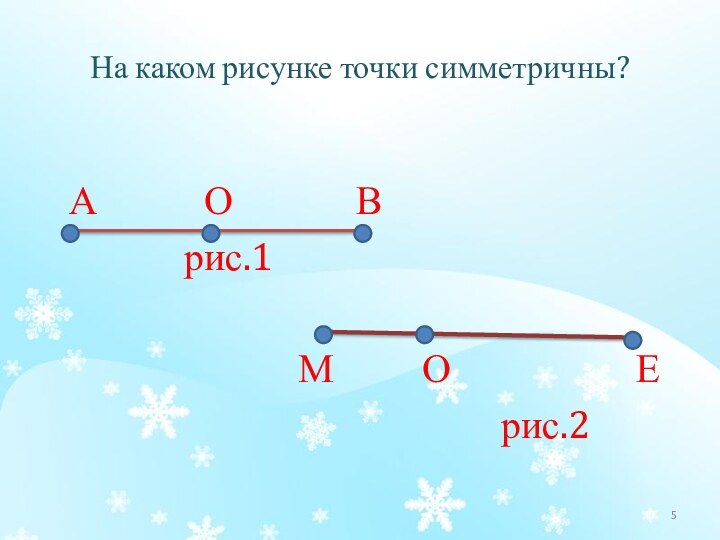
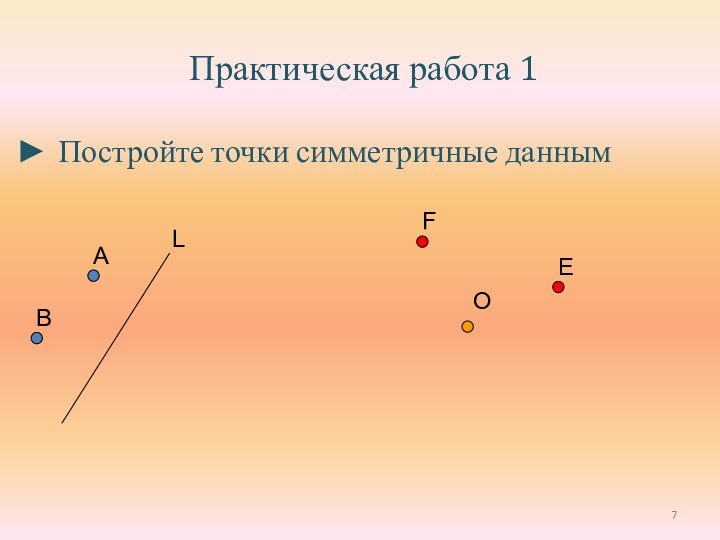
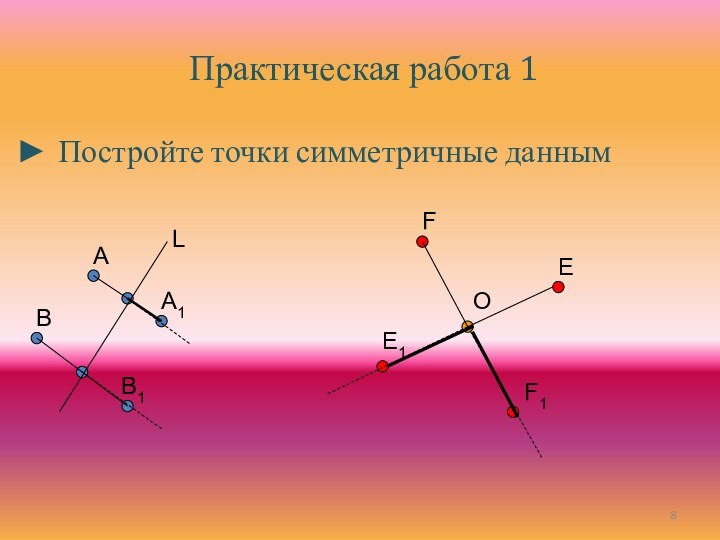
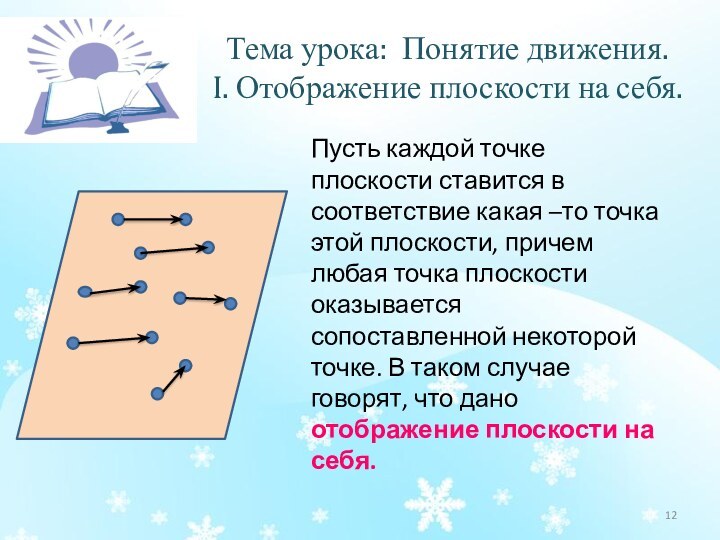
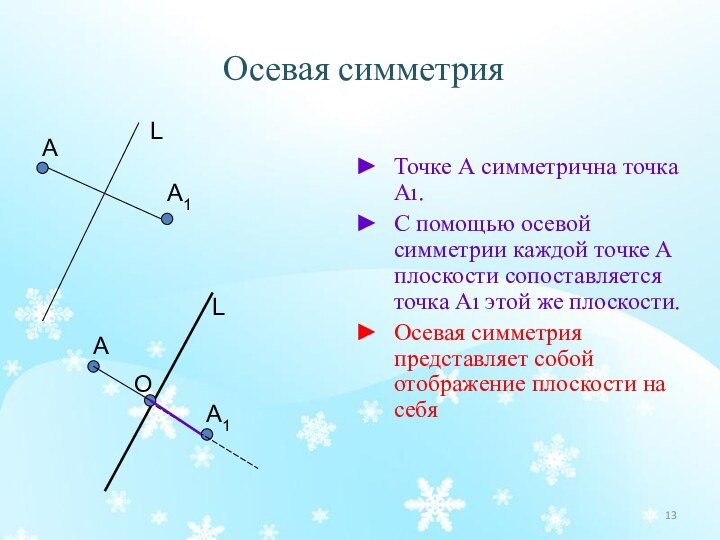
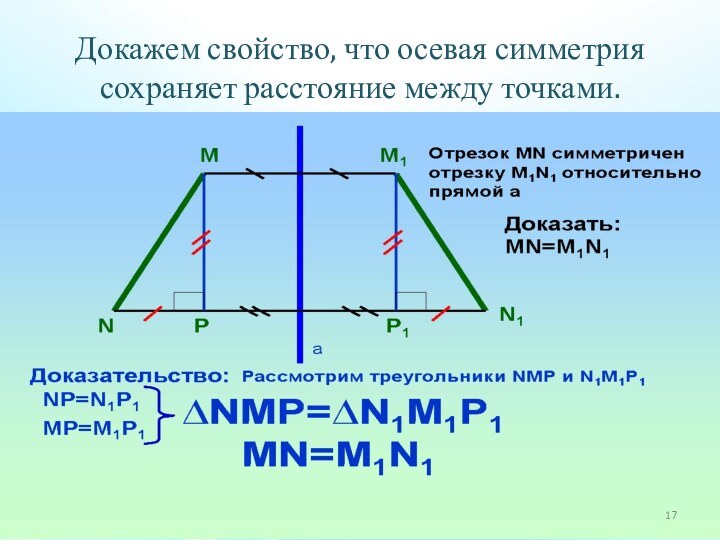
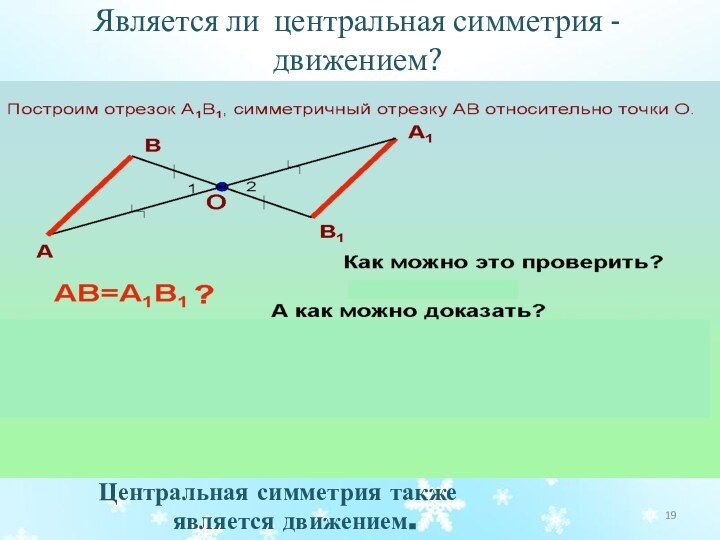
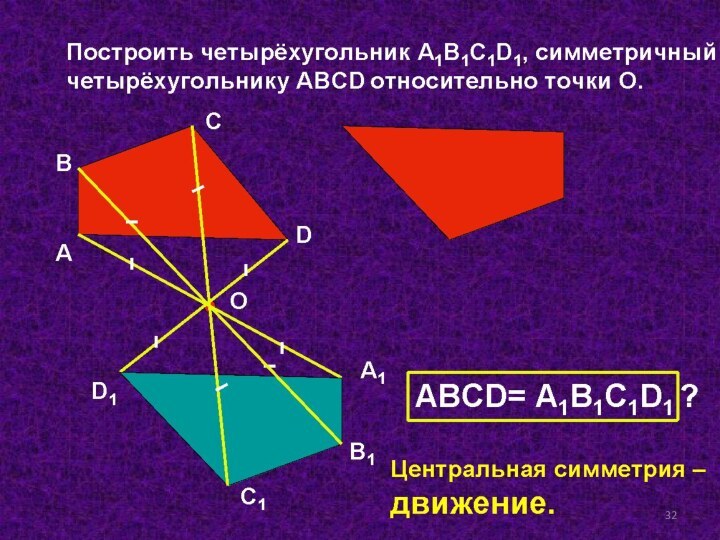
основы для введения понятие движения;
2)Ввести понятие движения и его

закрепить. 3) Познакомить учащихся с примерами геометрических преобразований; 4) Отработать навыки построения фигур при симметриях;
5)Развития познавательных интересов, интеллектуальных и творческих способностей в процессе решения геометрических задач и самостоятельного приобретения знаний в процессе работы.

симметричными относительно прямой, если эта прямая проходит через середину

отрезка и перпендикулярна ему.
Как называется такая симметрия?
Осевая симметрия.
Сколько осей симметрии имеет равнобедренный треугольник, равносторонний, прямоугольник, квадрат, окружность?
Одну, три, две, четыре, бесконечно много.
Какие точки называются симметричными относительно некоторой точки О?
Если точка О середина отрезка, заключенного между данными точками.
Как называется такая симметрия?
Центральная.
Какие фигуры обладают центральной симметрией?
Окружность, параллелограмм, прямоугольник, квадрат и т.д.

А О В
рис.1

М О Е
рис.2

О?
А
А1
О

каждой точке плоскости ставится в соответствие какая –то точка

этой плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.

осевой симметрии каждой точке А плоскости сопоставляется точка Аı

этой же плоскости.
Осевая симметрия представляет собой отображение плоскости на себя

А

L

А1

А

О

А1

L

1 относительно точки О.
С помощью центральной симметрии каждой точке

А плоскости сопоставляется точка Аı этой же плоскости.
Центральная симметрия представляет собой отображение плоскости на себя.

А

О

А1

А

О

А1

симметрия?


Отображение плоскости на себя, сохраняющее расстояние, называют

– движением.

о перемещении.  
Но, если говоря о перемещении, мы представляем себе непрерывный

процесс, то в геометрии для нас будут иметь значение только начальное и конечное положения фигур.

точками.

Центральная симметрия также

является движением.

отображается в точку

М1, точка N –
в точку N1.

Доказать: отрезок МN отображается в
отрезок М1N1.

M

N

M1

N1

1. Р

МN

P

2. MP + PN = MN

3. M1N1=MN,

M1P1=MP,

N1P1=NP

P1

4. M1P1+P1N1=MP+PN=MN=M1N1

т.е. M1P1+P1N1=M1N1

P1

M1N1

I.

II.

Докажем, что в каждую точку
Р1 отрезка М1N1 отображается
какая – нибудь точка Р отрезка
MN.

Т.к. Р1

М1N1,

то

M1N1=M1P1+P1N1=MP+PN=MN,

т.е P

MN

Теорема доказана.

=
А1В1С1

фигуру.

отображается:
1.
2.
3.
4.
5.

отрезок, треугольник – на равный ему треугольник, угол –

на равный ему угол.

Используя эти свойства движений, можно получить различные способы решений, а именно:

—> A1B1C1D1,
причем
ABCD = A1B1C1D1,
т.к.
∆ABD = ∆A1B1D1;
∆BCD = ∆B1C1D1

—>A1,
B —> B1,
C —> C1,
D —>D1,

причем

AB =A1B1,

AD =A1D1,

BC =B1C1,

CD =C1D1,

A =A1,

B = B1,

C =C1,

D = D1,

тогда

ABCD —> A1B1C1D1,

ABCD = A1B1C1D1

l.
O1
2. А1 симметрично А
относительно l.
А1
3. О1А1=ОА
Каждая точка

окружности отображается
в точку на окружности, симметричную
данной относительно прямой l.

точки,
симметричные друг другу относительно
оси l.
О1
О2
l
F
F1
R
R1

прямой a .

2. Постройте четырёхугольник А₁В₁С₁D₁ симметричен четырёхугольнику

АВСD относительно точки О.

симметрии представляют собой отображение плоскости на себя?
Каким важным свойством

обладает осевая симметрия?
Каким важным свойством обладает центральная симметрия?
В какую фигуру отобразится при движении : отрезок , луч, угол, треугольник, квадрат ?

Домашнее задание.

П.113,114 теорему учить, №1152(в,г),1159,1160.

протяжении веков пытался постичь и создать порядок, красоту и

совершенство". Г.Вейль.