- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Симметрия фигур
Содержание
- 2. ОглавлениеОбщее представление о преобразовании фигур.Общее представление о симметрии фигурВиды симметрииСимметрия относительно точкиСимметрия относительно прямой
- 3. Если каждую точку данной фигуры сместить каким-нибудь
- 4. Преобразование одной фигуры в другую называется движением,
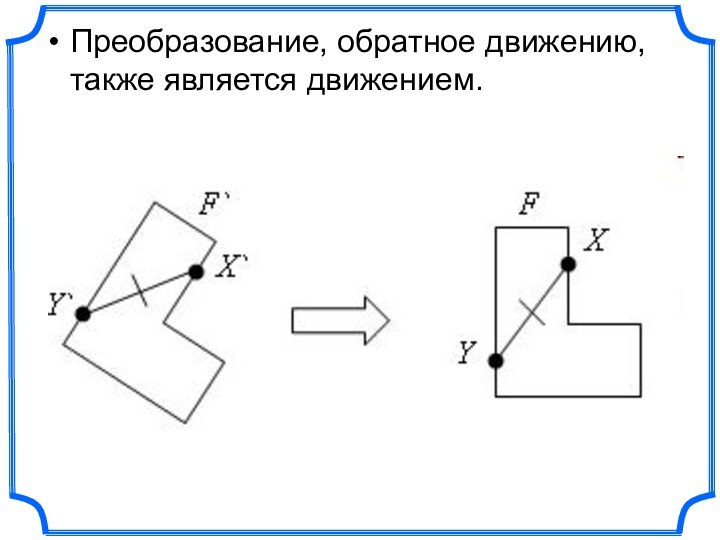
- 5. Преобразование, обратное движению, также является движением.
- 6. Симметрия в переводе с греческого означает соразмерность.
- 7. Существует множество различных видов симметрии. К простейшим
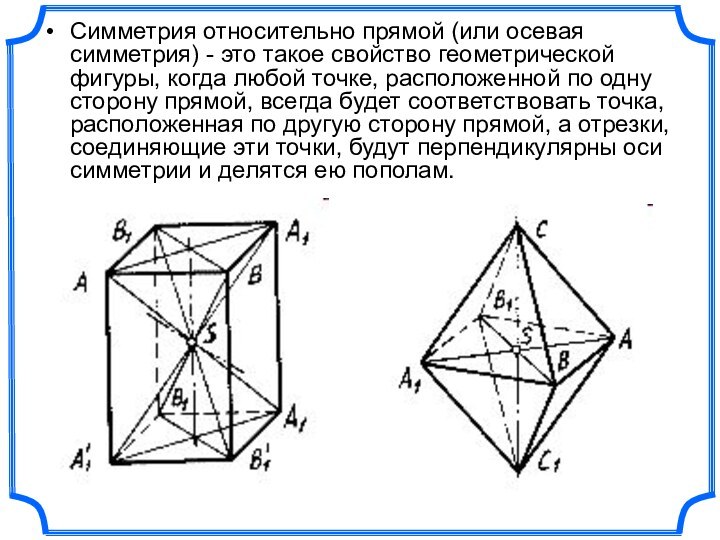
- 8. Симметрия относительно прямой (или осевая симметрия) -
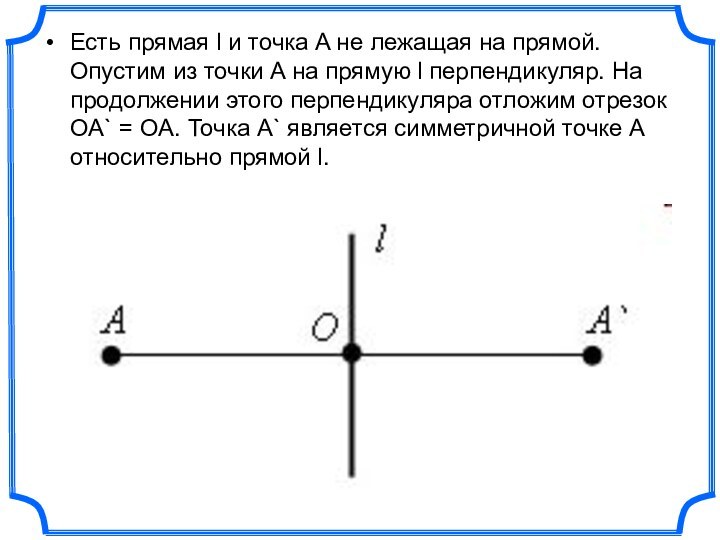
- 9. Есть прямая l и точка A не
- 10. Так ромб симметричен сам себе относительно своих диагоналей. Диагонали ромба являются его осями симметрии.
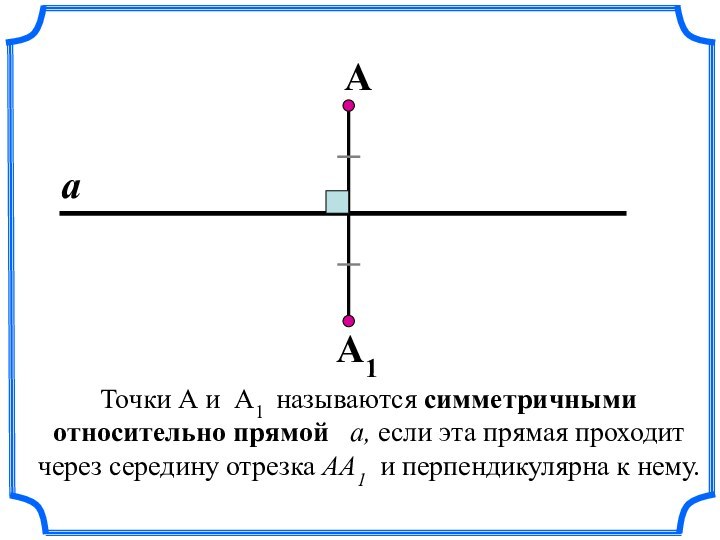
- 11. Точки А и А1 называются симметричными относительно
- 12. Точки М и М1 симметричны относительно прямой
- 13. Фигура называется симметричной относительно прямой a, если
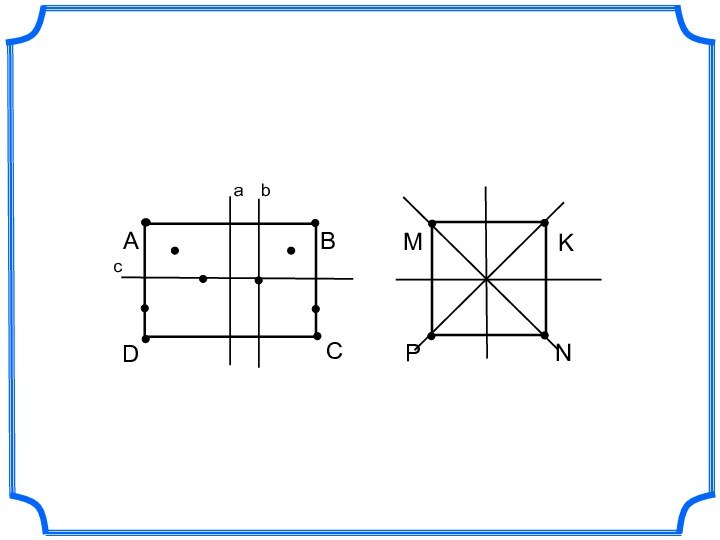
- 14. АDBCMKNPabc
- 15. Симметрия относительно точкиАОТочки А и А1 называются
- 16. А1АОПостроить отрезок А1В1 симметричный отрезку АВ относительно
- 17. А1ОПостроить луч симметричный лучуотносительно точки ОТочка О – центр симметрииa1aaa1Начало луча
- 18. А1Построить угол
- 19. ОАВВ1СС1А1Замечание. Если центр во внешней области фигуры, то исходная и симметричная фигура не имеют общих точек.
- 20. АВСЗамечание. Если центр во внутренней области фигуры, то исходная и симметричная фигура имеют общие точки (6-угольник).
- 21. АВСЗамечание. Если центр на стороне фигуры, то исходная и симметричная фигура имеют общие точки (отрезок СС1).
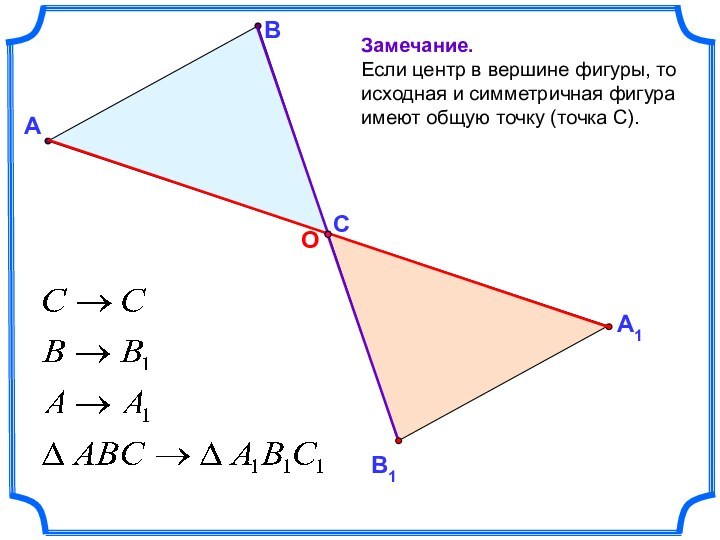
- 22. АВЗамечание. Если центр в вершине фигуры, то исходная и симметричная фигура имеют общую точку (точка С).С
- 24. ОБулавин Павел, 9В класс.т. О – центр симметрии
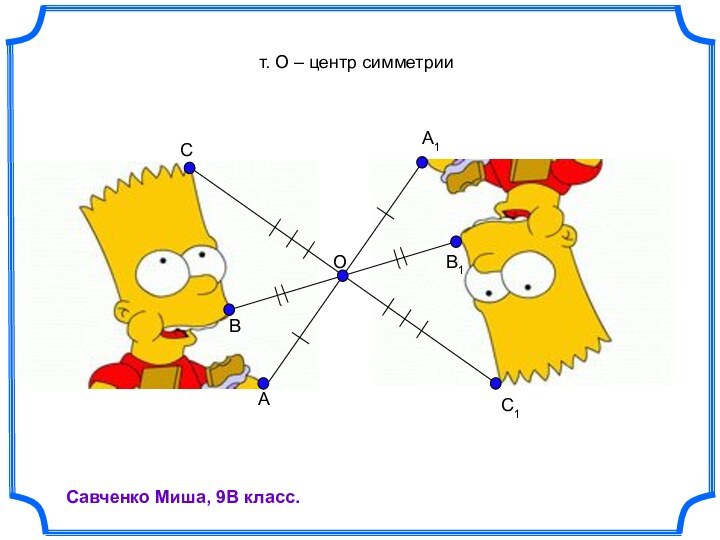
- 25. OAC1A1BB1CСавченко Миша, 9В класс.т. О – центр симметрии
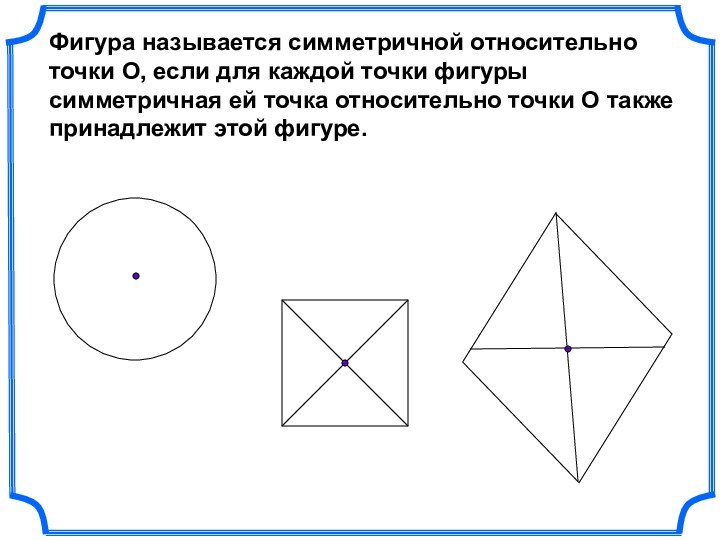
- 26. Фигура называется симметричной относительно точки О, если
- 30. http://www.point.ru/photo/galleries/12876/
- 31. Скачать презентацию
- 32. Похожие презентации
ОглавлениеОбщее представление о преобразовании фигур.Общее представление о симметрии фигурВиды симметрииСимметрия относительно точкиСимметрия относительно прямой

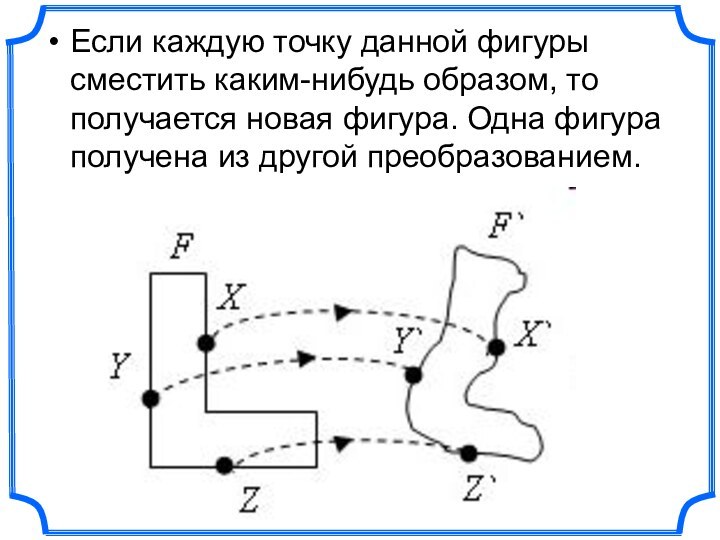















Слайд 3 Если каждую точку данной фигуры сместить каким-нибудь образом,
то получается новая фигура. Одна фигура получена из другой
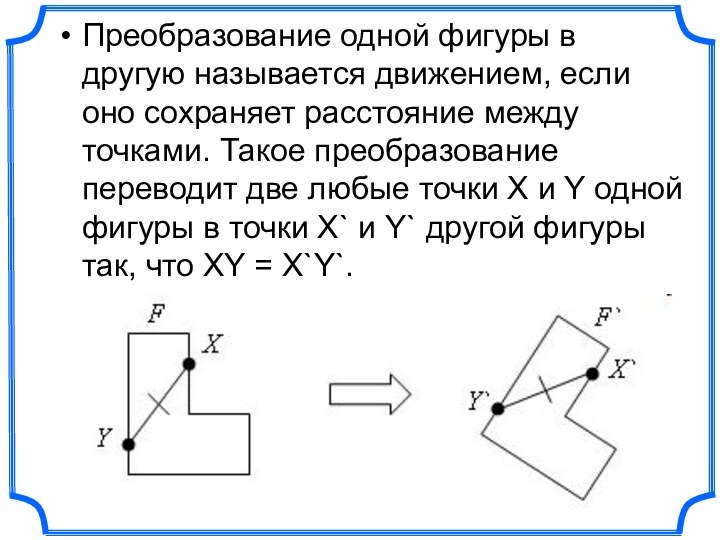
преобразованием.Слайд 4 Преобразование одной фигуры в другую называется движением, если
оно сохраняет расстояние между точками. Такое преобразование переводит две
любые точки X и Y одной фигуры в точки X` и Y` другой фигуры так, что XY = X`Y`.Слайд 6 Симметрия в переводе с греческого означает соразмерность. Под
симметрией принято понимать свойство геометрической фигуры, расположенной в пространстве
или на плоскости, заключающееся в закономерном повторении равных ее частей. Изучение видов симметрии имеет большое практическое и теоретическое значение для различных областей науки и техники и, особенно, при изучении строения кристаллических веществ.Слайд 7 Существует множество различных видов симметрии. К простейшим из
них относятся:
а) симметрия
относительно плоскости (зеркальная симметрия);б) симметрия относительно точки (центральная симметрия);
в) симметрия относительно прямой (осевая симметрия);
г) симметрия вращения;
д) цилиндрическая симметрия;
е) сферическая симметрия.
Слайд 8 Симметрия относительно прямой (или осевая симметрия) - это
такое свойство геометрической фигуры, когда любой точке, расположенной по
одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.Слайд 9 Есть прямая l и точка A не лежащая
на прямой. Опустим из точки A на прямую l
перпендикуляр. На продолжении этого перпендикуляра отложим отрезок OA` = OA. Точка A` является симметричной точке A относительно прямой l.Слайд 10 Так ромб симметричен сам себе относительно своих диагоналей.
Диагонали ромба являются его осями симметрии.
Слайд 11 Точки А и А1 называются симметричными относительно прямой
a, если эта прямая проходит через середину отрезка АА1
и перпендикулярна к нему.
А
А1
а
Слайд 12
Точки М и М1 симметричны относительно прямой с.
М
М1
с
Что можно сказать о точках М и М1?
Точка Р симметрична сама себе
относительно прямой с.
Р
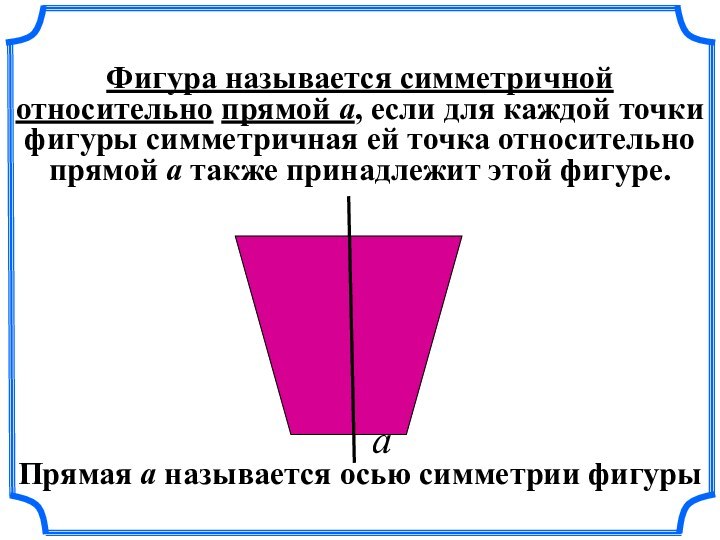
Слайд 13 Фигура называется симметричной относительно прямой a, если для
каждой точки фигуры симметричная ей точка относительно прямой а
также принадлежит этой фигуре.а
Прямая а называется осью симметрии фигуры
Слайд 15
Симметрия относительно точки
А
О
Точки А и А1 называются симметричными
относительно точки О (центр симметрии), если О – середина
отрезка АА1.Точка О считается симметричной самой себе.
Точка О – центр симметрии
Симметрия относительно точки называется центральной симметрией
Слайд 16
А1
А
О
Построить отрезок А1В1 симметричный отрезку АВ относительно точки
О
Точка О –
центр симметрии
В
Замечание:
при симметрии относительно центра
изменился порядок точек (верх-низ, право-лево).Например, точка А отобразилась снизу вверх; она была правее точки В, а ее образ точка А1 оказалась левее точки В1.
Слайд 17
А1
О
Построить луч симметричный лучу
относительно точки
О
Точка О –
центр симметрии
a1
a
a
a1
Начало луча
Слайд 18
А1
Построить угол
симметричный углу
относительно точки О
Точка О –
центр
симметрииa1b1
a
a1
Вершина угла
ab
∠
∠
b
О
Слайд 19
О
А
В
В1
С
С1
А1
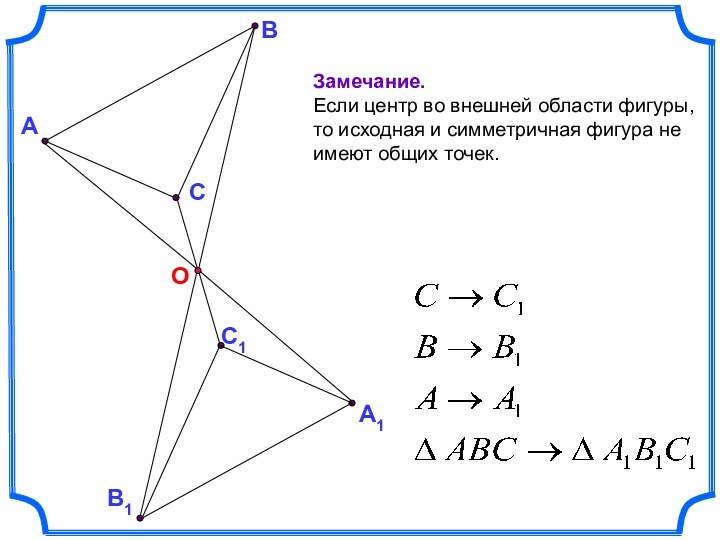
Замечание.
Если центр во внешней области фигуры, то
исходная и симметричная фигура не имеют общих точек.
Слайд 20
А
В
С
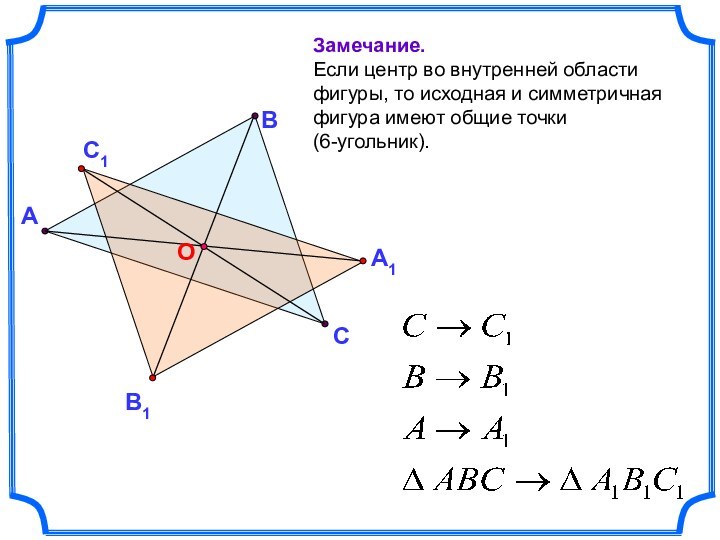
Замечание.
Если центр во внутренней области фигуры, то
исходная и симметричная фигура имеют общие точки
(6-угольник).
Слайд 21
А
В
С
Замечание.
Если центр на стороне фигуры, то исходная
и симметричная фигура имеют общие точки (отрезок СС1).
Слайд 22
А
В
Замечание.
Если центр в вершине фигуры, то исходная
и симметричная фигура имеют общую точку (точка С).
С
Слайд 26 Фигура называется симметричной относительно точки О, если для
каждой точки фигуры симметричная ей точка относительно точки О
также принадлежит этой фигуре.