правильные многоугольники и, кроме того, в каждой вершине сходится
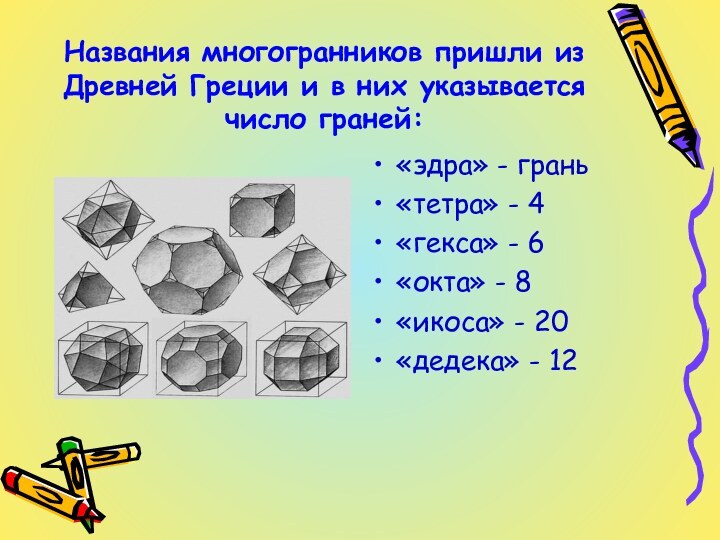
одинаковое число рёбер. Существует 5 видов правильных многогранников.ТЕТРАЭДР
ГЕКСАЭДР
ОКТАЭДР
ИКОСАЭДР
ДОДЕКАЭДР
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






ТЕТРАЭДР
ГЕКСАЭДР
ОКТАЭДР
ИКОСАЭДР
ДОДЕКАЭДР
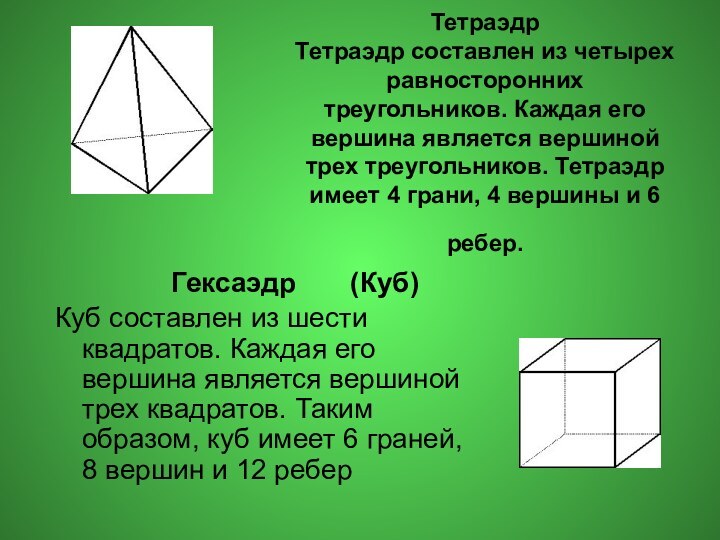
Гексаэдр (Куб)
Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер
Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Икосаэдр имеет 20 граней, 12 вершин и 30 ребер
В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2.
Г+В=Р+2