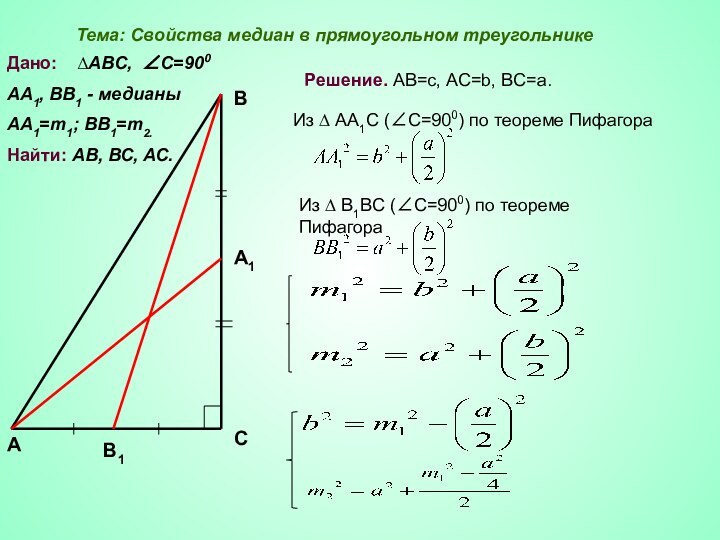
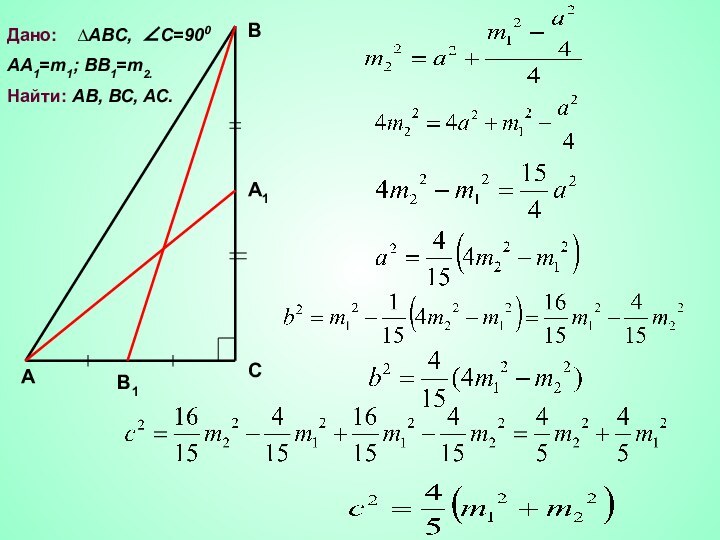
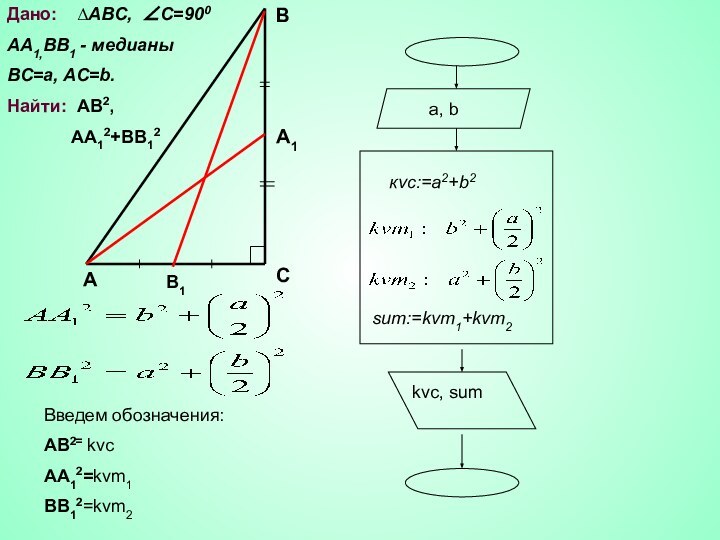
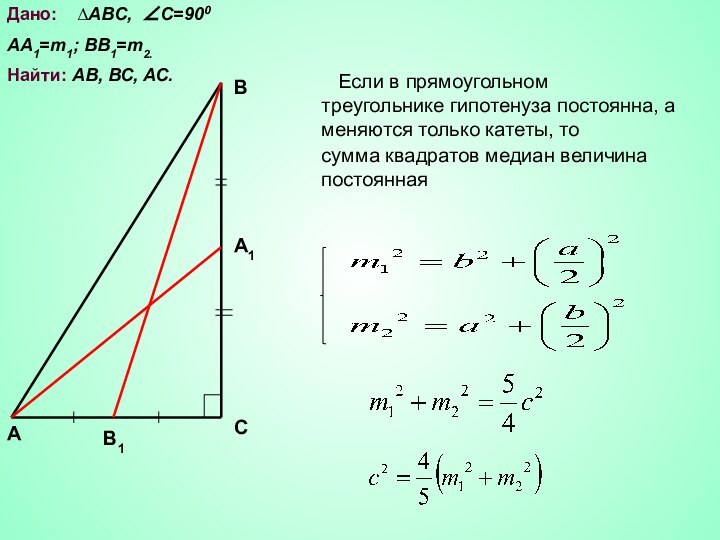
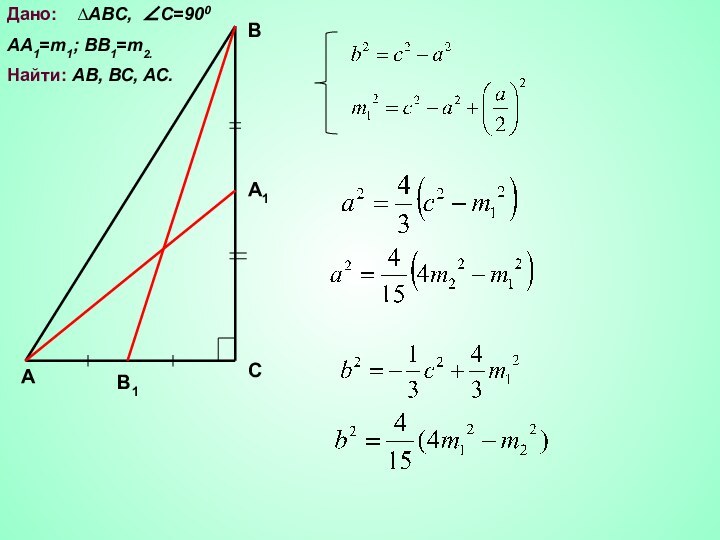
АВ, ВС, АС.
Решение. АВ=с, АС=b, BC=a.
Из ∆ АА1С (∠С=900)
по теореме ПифагораИз ∆ B1BС (∠С=900) по теореме Пифагора
Тема: Свойства медиан в прямоугольном треугольнике
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

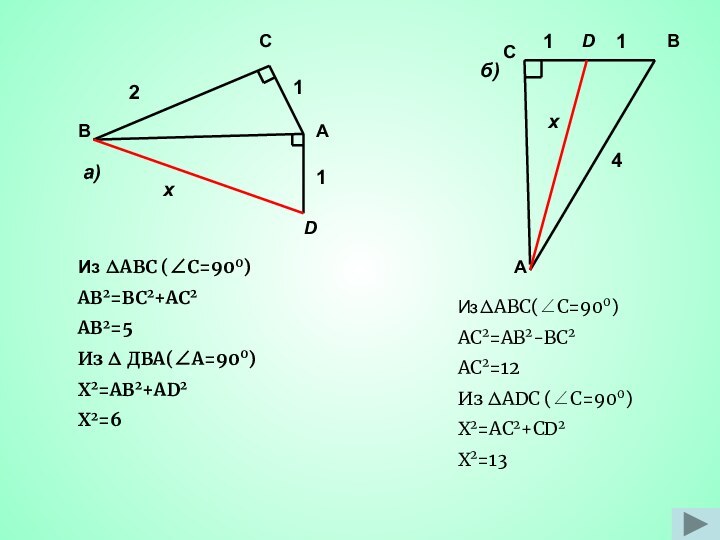
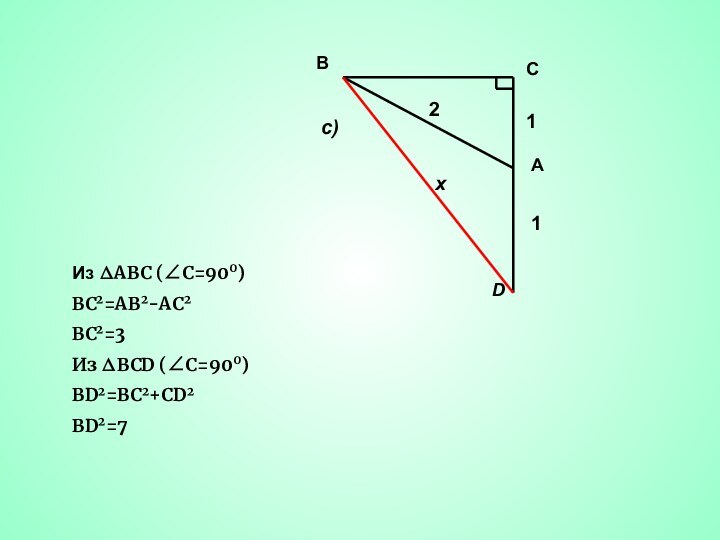
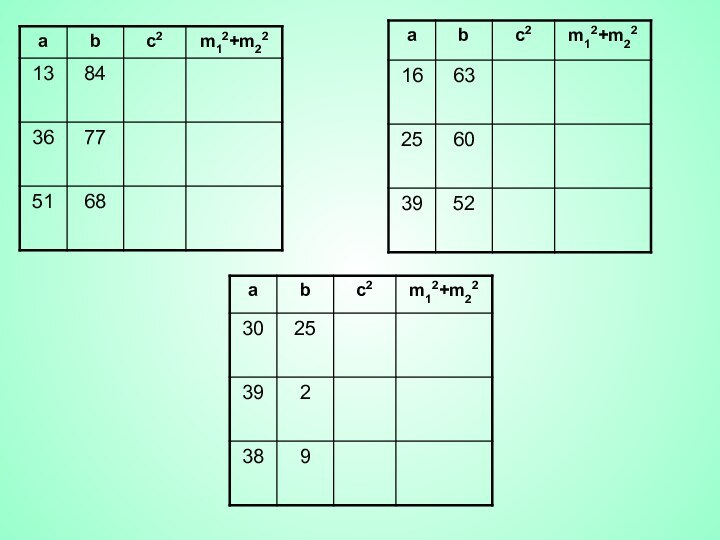
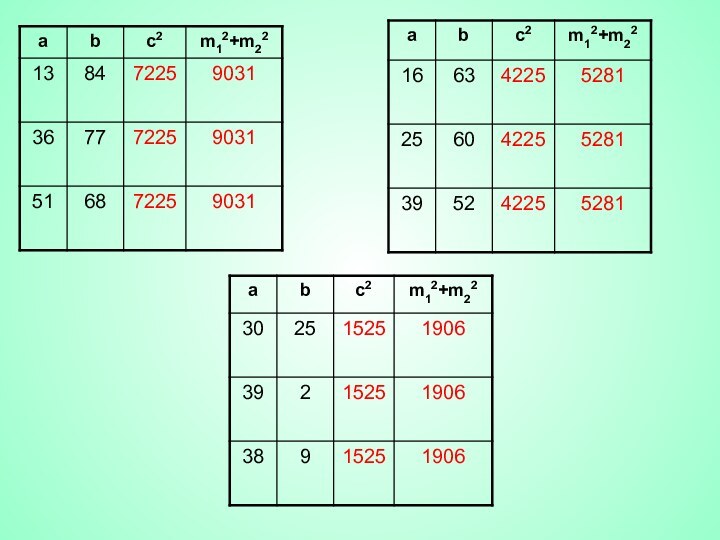

Из ∆ B1BС (∠С=900) по теореме Пифагора
Тема: Свойства медиан в прямоугольном треугольнике
sum:=kvm1+kvm2
kvc, sum
кvc:=а2+b2
Введем обозначения:
AB2= kvc
AA12=kvm1
ВВ12=kvm2
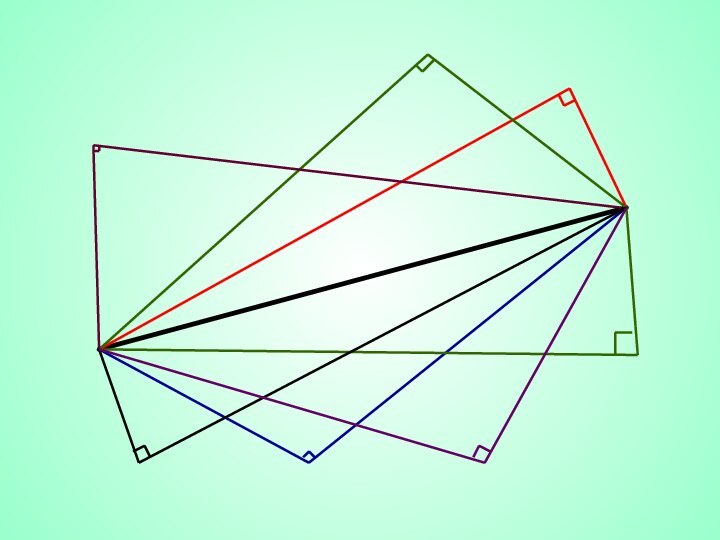
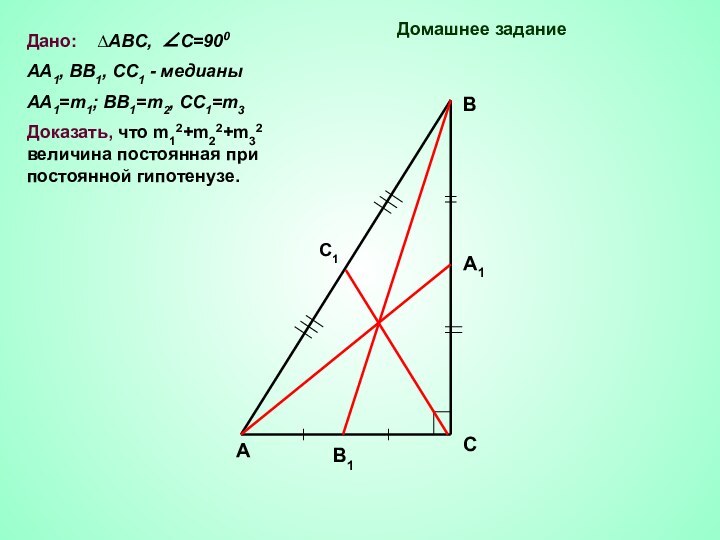
сумма квадратов медиан величина постоянная