Слайд 2
Четырёхугольник — это многоугольник, содержащий четыре вершины, четыре
стороны и четыре угла.
А
В
С
D
AB, BC, CD, AD –
стороны
A,
B, C, D –
вершины
∠ABC , ∠ BCD, ∠ CDA, ∠ DAB -
углы
Слайд 3
1) Две несмежные стороны четырехугольника называются противоположными сторонами
(например,
ВС и АD).
2) Две вершины, не являющиеся соседними,
называются также противоположными вершинами
(например, С и А).
А
В
С
D
Слайд 4
3) Стороны, исходящие из одной вершины, называются смежными
сторонами. (Например, АВ и ВС).
4) Вершины, являющиеся концами одной
стороны, называются соседними . (Например, А и В).
А
В
С
D
5) Отрезки, соединяющие противоположные вершины, называются диагоналями.
А
В
С
D
Слайд 5
1. Никакие три вершины четырёхугольника
не лежат на одной прямой.
2. Каждая
вершина является общим концом двух и только двух сторон.
3. Стороны четырехугольника не имеют других точек
пересечения кроме вершин.
А
В
С
D
Замечания.
Слайд 6
Выпуклые и невыпуклые четырёхугольники.
ABCD — выпуклый четырёхугольник,
он лежит по одну сторону от каждой прямой, проходящей
через его соседние вершины.
A1B1C1D1 — невыпуклый четырёхугольник (вогнутый), он лежит по разные стороны от каждой прямой, проходящих через две его соседние вершины.
A
B
C
D
A1
B1
C1
D1
Слайд 7
Выпуклый четырёх-угольник
Параллелограмм
Ромб
Квадрат
Прямоугольник
Трапеция
Равнобедренная трапеция
Прямоугольная трапеция
Слайд 9
А
В
С
D
ABC + BCD + CDA +
DAB = 360
Теорема о сумме углов четырехугольника:
«Сумма углов
четырёхугольника
равна 360»
Слайд 10
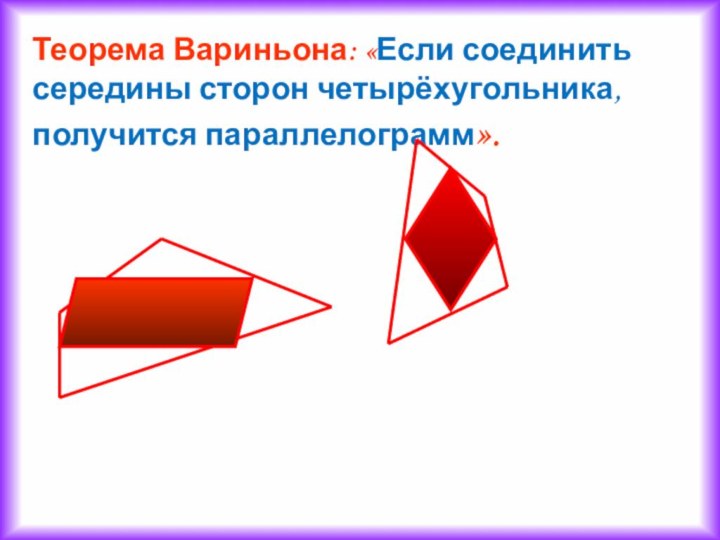
Теорема Вариньона: «Если соединить середины сторон четырёхугольника, получится
Слайд 11
Теорема Птолемея: «В выпуклом четырёхугольнике, вписанном в окружность,
произведение диагоналей равно сумме произведений противоположных сторон».
BD ·AC =
AB · CD + BC · AD
А
В
С
D
Слайд 13
А
В
С
D
Вписанный четырёхугольник –
это четырёхугольник, у которого все
его вершины
лежат на окружности.
Слайд 14
Замечание.
Четырёхугольник можно вписать в окружность, если сумма противоположных
углов равна 180°
( ∠A+ ∠ C= ∠ B+
∠ D=180° ).
А
В
С
D
Слайд 15
2) Описанный четырёхугольник –
это четырёхугольник, у которого
все его стороны
касаются этой окружности.
A
B
C
D
Слайд 16
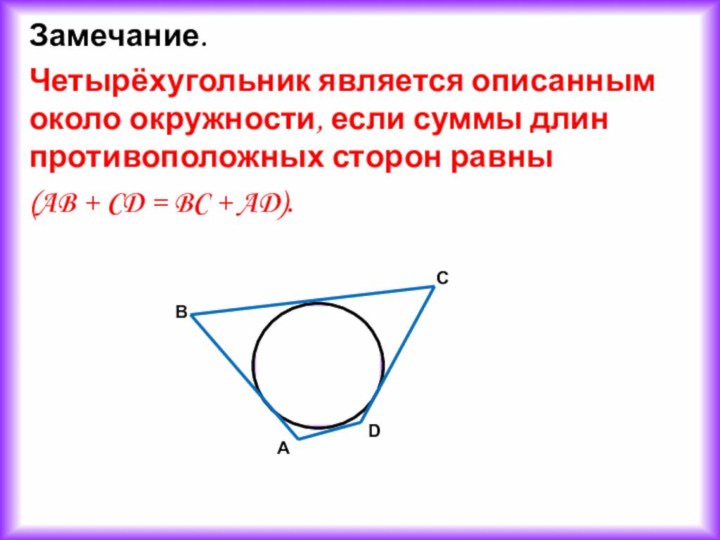
Замечание.
Четырёхугольник является описанным около окружности, если суммы длин
противоположных сторон равны
(AB + CD = BC +
AD).
A
B
C
D
Слайд 17
A
B
C
D
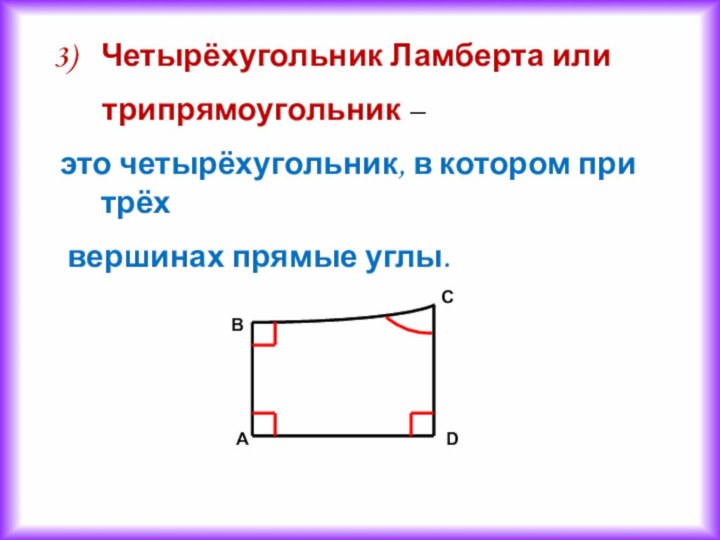
Четырёхугольник Ламберта или
трипрямоугольник –
это четырёхугольник, в котором при трёх
вершинах прямые углы.
Слайд 19
Теорема 1: «Площадь произвольного выпуклого четырёхугольника равна половине
произведения диагоналей на синус угла между ними».
А
В
С
D
О
Слайд 20
Теорема 2 (формула Герона): «Площадь вписанного четырёхугольника вычисляется
по формуле (где р – полупериметр)
A
B
C
D
a
b
c
d
Слайд 21
Четырехугольники, изучаемые в школе.
Слайд 22
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно
параллельны.
1). Параллелограмм.
А
В
С
D
AB||CD, BC||AD
Слайд 23
Свойство 1.
Диагонали параллелограмма точкой пересечения
делятся пополам.
О
ABCD (AB||CD,
BC||AD)
AC и BD – диагонали
AC ∩ BD =
O
Значит:
AO=OC
BO=OD
А
В
С
D
О
Слайд 24
Свойство 2.
В параллелограмме противоположные стороны равны
и противоположные
углы равны.
О
ABCD (AB||CD, BC||AD)
Значит:
AВ=DC
BC=AD
∠BAD = ∠BCD
∠ABC =
∠CDA
А
В
С
D
Слайд 25
Свойство 3.
В параллелограмме сумма углов, прилежащих к одной
стороне, равна 180°.
О
ABCD (AB||CD, BC||AD)
Значит:
∠BAD + ∠АDС=180°
(например).
А
В
С
D
Слайд 26
Свойство 4.
В параллелограмме сумма квадратов
диагоналей равна сумме
квадратов всех
сторон.
О
ABCD (AB||CD, BC||AD)
AC и BD – диагонали
AC ∩ BD = O
Значит:
А
В
С
D
О
AC² + BD² =
=AB² + BC² + CD² + DA²
Слайд 27
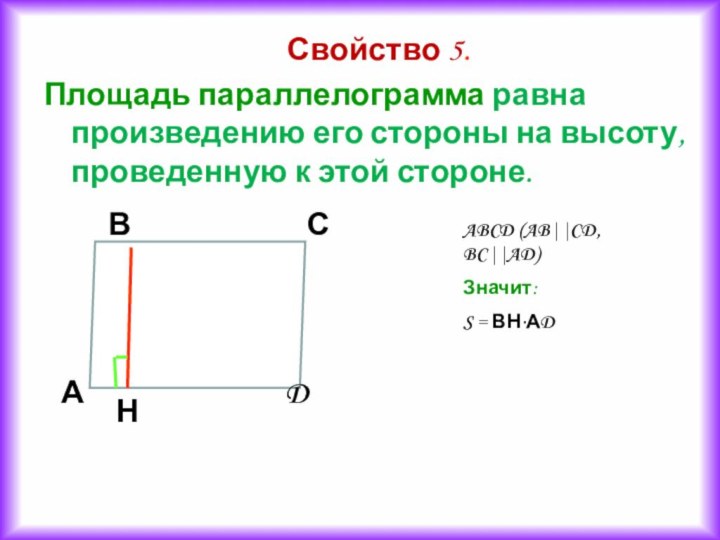
Свойство 5.
Площадь параллелограмма равна произведению его стороны на
высоту, проведенную к этой стороне.
О
ABCD (AB||CD, BC||AD)
Значит:
S =
ВН·АD
А
В
С
D
Н
Слайд 28
Признак 1.
Если в четырёхугольнике две стороны равны и
параллельны, то этот четырёхугольник –
параллелограмм.
О
А
В
С
D
Если
ABCD – четырёхугольник
AB||CD,
AB = CD,
то
ABCD (AB||CD, BC||AD).
Слайд 29
Признак 2.
Если в четырёхугольнике противоположные стороны
попарно равны,
то этот четырёхугольник –
параллелограмм.
О
А
В
С
D
Если
ABCD – четырёхугольник
ВС = АD,
AB = CD,
то
ABCD (AB||CD, BC||AD).
Слайд 30
Признак 3.
Если в четырёхугольнике диагонали пересекаются и
точкой
пересечения делятся пополам, то этот
четырёхугольник – параллелограмм.
О
А
В
С
D
Если
ABCD –
четырёхугольник
ВО = ОD, AО= CО,
то
ABCD (AB||CD, BC||AD).
О
Слайд 31
Прямоугольником называется параллелограмм, у которого есть прямой угол.
2).
Прямоугольник.
А
В
С
D
AB||CD, BC||AD и ∠А= ∠ В= ∠ С= ∠
D=90°
Слайд 32
Свойства.
Прямоугольник обладает всеми свойства параллелограмма:
- диагонали прямоугольника точкой
пересечения делятся пополам,
- в прямоугольнике противоположные стороны равны и
противоположные углы равны,
- в прямоугольнике сумма углов, прилежащих к одной стороне, равна 180°,
- в прямоугольнике сумма квадратов диагоналей равна сумме квадратов всех сторон.
Слайд 33
Прямоугольник обладает особыми свойствами:
диагонали прямоугольника равны,
- прямоугольник имеет
две оси симметрии, которые проходят через точки пересечения диагоналей
параллельно его сторонам.
А
В
С
D
AC = BD
А
В
С
D
Слайд 34
А
В
С
D
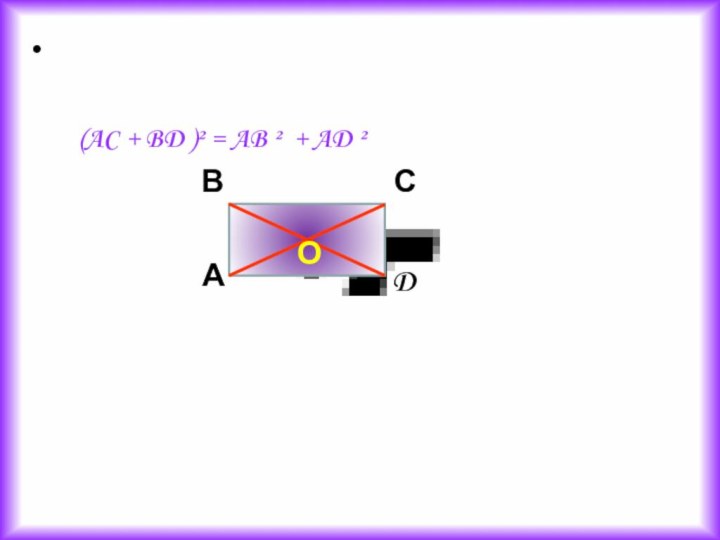
(AC + BD )² = AB ² +
AD ²
О
Слайд 35
Признак.
Если в параллелограмме диагонали равны, то этот параллелограмм–
прямоугольник.
А
В
С
D
Если
в параллелограмме AC = BD,
то
это прямоугольник.
Слайд 36
Замечание.
В прямоугольнике стороны находятся в отношении золотого сечения.
Этот прямоугольник содержит в себе квадрат и малый прямоугольник
золотого сечения (его большая сторона является малой стороной первоначального прямоугольника.)
Поэтому можно построить прямоугольник золотого сечения на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится прямоугольник золотого сечения, как показано на 2 рисунке.
Слайд 37
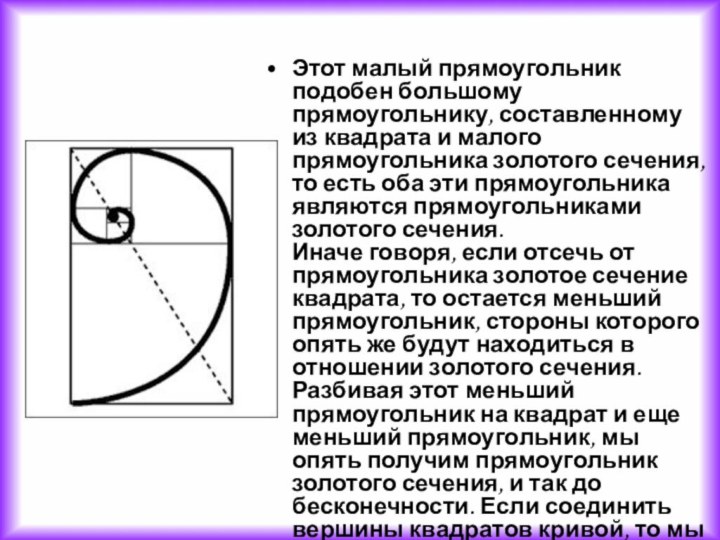
Этот малый прямоугольник подобен большому прямоугольнику, составленному из
квадрата и малого прямоугольника золотого сечения, то есть оба
эти прямоугольника являются прямоугольниками золотого сечения.
Иначе говоря, если отсечь от прямоугольника золотое сечение квадрата, то остается меньший прямоугольник, стороны которого опять же будут находиться в отношении золотого сечения. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник золотого сечения, и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют "кривая развития", "спираль жизни", ибо в ней как бы заложена идея бесконечного развития
Слайд 38
Бесконечное повторение прямоугольника золотого сечения и квадрата при
рассечении прямоугольника золотого сечения обнаруживает повторение целого в его
частях, что является одним из условий гармонии целого. Это свойство прямоугольника золотого сечения было обнаружено художниками, и они стали употреблять золотое сечение как способ гармонизации, способ пропорционирования. Фидий использовал золотое сечение . при постройке Акрополя (5 век до н. э. ).
Греческие ремесленники, создавая гончарные изделия также применяли золотое сечение. В эпоху Возрождения золотое сечение использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли золотое сечение в поисках гармоничных пропорций букв.
Слайд 39
Прямоугольник золотого сечения мы встречаем и в пропорциях
средневековых рукописных книг, и в современной книге, так как
стройные пропорции золотого сечения позволяют красиво организовать пространство книжной страницы и разворота.
Слайд 40
Квадратом называется прямоугольник, у которого все стороны равны.
3).
Квадрат.
А
В
С
D
AB=CD, BC=AD
Слайд 41
Квадрат - правильный четырёхугольник. Может быть определён как
прямоугольник, у которого две смежные стороны равны или как
ромб, у которого все углы прямые.
Квадрат обладает всеми свойства параллелограмма, прямоугольника, ромба.
Замечания.
А
В
С
D
Слайд 42
3. Сумма квадратов диагоналей квадрата равна учетверённому квадрату
его стороны:
4. Длина диагонали:
А
В
С
D
AC² + BD² = 4 ·
AB²
d= a
5. Пусть а - сторона квадрата, R - радиус описанной окружности, r - радиус вписанной окружности. Тогда периметр квадрата равен:
P = 4а=4 R² = 8r
а
R
r
Слайд 43
3. Площадь квадрата равна квадрату его стороны:
4. Если
прямоугольник и квадрат имеют одинаковые периметры , то наибольшую
площадь будет иметь квадрат.
5. В квадрате есть золотое сечение. Один из видов золотого сечения - это модульная сетка.
А
В
С
D
Слайд 44
Модульная сетка определяет размеры полей и формат полосы
набора. Конечно, модульная сетка, постольку, поскольку имеет дело с
печатными изданиями, должна учитывать размеры строк, высоту литер, пробельные элементы в типографских мерах (квадраты, цицеро, пункты), чтобы правильно располагать печатный материал на странице.
Система сеток благодаря четкой модульной основе позволяет ввести в процесс проектирования издания электронные программы.
В прикладной, промышленной графике модульную сетку применяют при конструировании всевозможных рекламных изданий и, в особенности при проектировании графического фирменного стиля. Модульную сетку применяют при конструировании различных знаков, знаков визуальных коммуникаций, товарных знаков и др.
Слайд 45
В основу модульных сеток часто бывает положен квадрат.

Квадрат очень удобный модуль. Он широко используется как модуль
в современной мебельной промышленности, в особенности, при конструировании сборной мебели, "стенок".
Двойной квадрат издавна известен как модуль традиционного японского дома, где размеры комнат находились в соответствии с тем, сколько раз уложится на полу циновка-татами имеющая пропорции двойного квадрата.
В прикладной графике квадрат используется для форматов проспектов альбомов, детских книг, но он также определяет и внутреннее пространство этих изданий. Квадратный модуль может использоваться и не в квадратном формате.
Приведем пример использования квадратного модуля в квадратном формате: при трехколоночном наборе текста вся площадь, отведенная под текст и иллюстрации, делится на 9 квадратов. Если ширину колонки обозначить 1, то квадрат будет 1х1. Иллюстрации при этом могут занимать площади: 1х1, 1х2, 1хЗ, 2х2, 2хЗ, ЗхЗ, 2х1, и т. д., то есть мы будем иметь достаточно широкие возможности для комбинирования иллюстраций и текста в верстке.
Слайд 46
На рисунке Леонардо да Винчи изображена связь квадрата
и круга с человеческой фигурой известная еще древним (Витрувий).
Художники Возрождения - немец Дюрер, итальянец Пачоли, француз Тори, занимаясь разработкой начертания букв, исходили из формы квадрата, буква со всеми своими элементами вписывалась в квадрат (рис. 12), хотя и не все буквы приравнивались к квадрату, однако общий композиционный строй определялся квадратом. Квадрат является устойчивой, статичной фигурой. Она ассоциируется с чем-то неподвижным, завершенным. В Древнем мире у некоторых народов изображение квадрата было связано с символикой смерти. (В этой связи интересно заметить, что пропорции квадрата в природе встречаются в формах неживой материи, у кристаллов). Благодаря своей статической завершенности квадрат используется в прикладной графике, в области визуальных коммуникаций наряду с формой круга как элемент, фиксирующий внимание, а также для ограничения пространства, на котором сосредоточена информация
Слайд 47
Ромбом называется параллелограмм, у которого все стороны равны.
4).
Ромб.
А
В
С
D
AB=CD=BC=AD
Слайд 48
Свойства.
Ромб обладает всеми свойства параллелограмма:
- диагонали ромба точкой
пересечения делятся пополам,
- в ромбе противоположные стороны равны и
противоположные углы равны,
- в ромбе сумма углов, прилежащих к одной стороне, равна 180°,
- в ромбе сумма квадратов диагоналей равна учетверённому квадрату стороны:
AC² + BD² = 4 ·AB²
Слайд 49
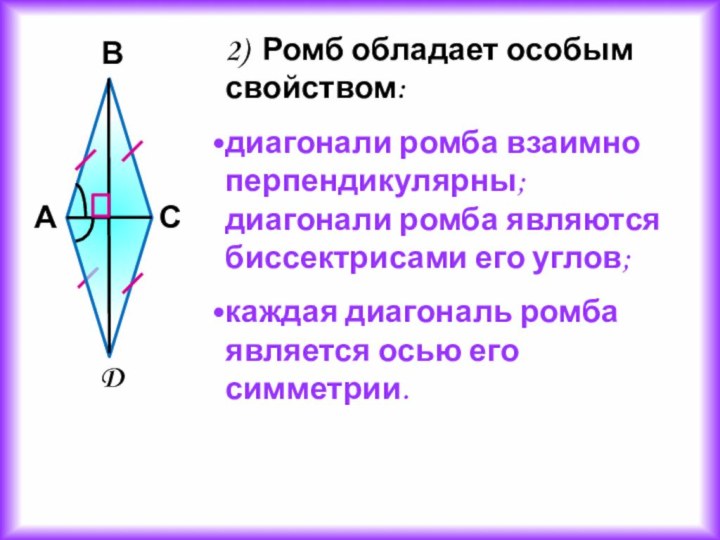
2) Ромб обладает особым свойством:
диагонали ромба взаимно перпендикулярны;
диагонали
ромба являются биссектрисами его углов;
каждая диагональ ромба является
осью его симметрии.
А
В
С
D
Слайд 50
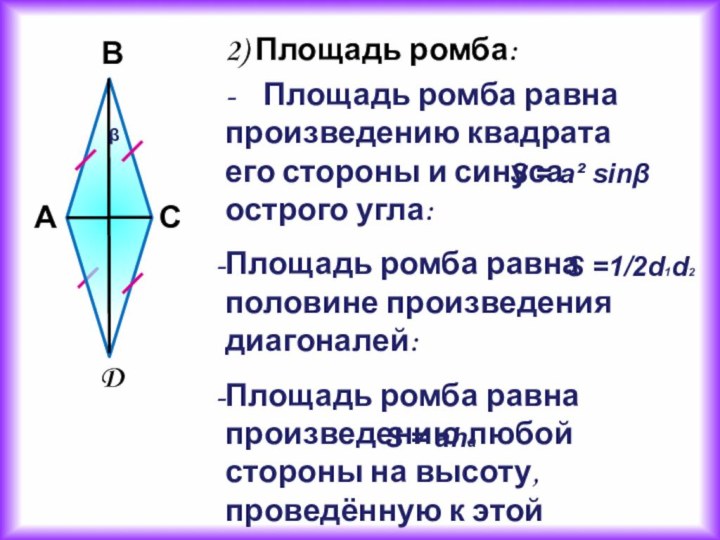
2) Площадь ромба:
- Площадь ромба равна произведению
квадрата его стороны и синуса острого угла:
Площадь ромба равна
половине произведения диагоналей:
Площадь ромба равна произведению любой стороны на высоту, проведённую к этой стороне:
А
В
С
D
S = a² sinβ
β
S =1/2d1d2
S = aha
Слайд 51
Признаки.
1. Если в параллелограмме диагонали перпендикулярны, то он
- ромб.
2. Если в параллелограмме диагонали являются биссектрисами его
углов, то он - ромб.
3. Параллелограмм является ромбом, если две его смежные стороны равны.
А
В
С
D
Слайд 52
Создателей этой загадочной фигуры, которая изображена на этой
странице, вдохновил вид скрещивающихся ферм, поддерживающих лестничную площадку в
двухэтажном доме. Опять же принцип трибара здесь очевиден. Эта фигура представляет собой не что иное, как два трибара, соединенных вместе в форме ромба. Вы можете расширить эту конструкцию, присоединяя дополнительные трибары. Эшер в своей знаменитой композиции соединил вместе три трибара. Здесь нет никаких ограничений. Теоретически можно соединить много таких трибаров по образцу лоскутного одеяла или другого дизайна. Во всяком случае, мы предоставим читателю самому пририсовывать треугольники к этой коварной квадратной квазифигуре!
Замечание.
Перекрещенный ромб.
Слайд 53
Трапецией называется четырёхугольник, у которого две стороны параллельны,
а две другие стороны не параллельны.
5). Трапеция.
А
В
С
D
Слайд 54
А
В
С
D
BC||AD, AB || CD
Боковая сторона
Основание
Боковая сторона
Основание
Средняя линия
Параллельные стороны
трапеции называются ее основаниями, а непараллельные стороны — боковыми
сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
Слайд 55
Равнобедренная трапеция – это трапеция, у которой непараллельные
стороны равны.
Прямоугольная трапеция – это трапеция, у которой один
из углов прямой.
A
B
C
D
AB = CD
A
B
C
D
Особые виды трапеций.
Слайд 56
1. Если трапеция равнобокая, то ее диагонали
равны и углы при основании равны.
2. Если трапеция равнобокая,
то около неё можно описать окружность.
А
В
С
D
BD = AC
BAD = CDA
Свойства.
A
B
C
D
Слайд 57
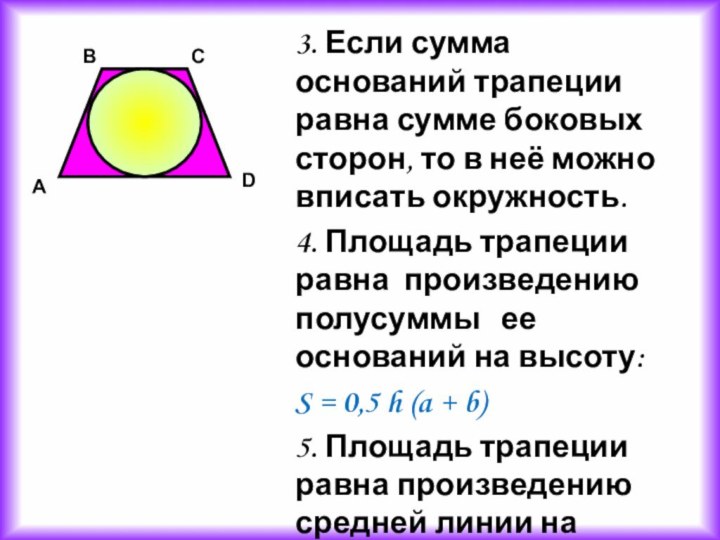
3. Если сумма оснований трапеции равна сумме
боковых сторон, то в неё можно вписать окружность.
4. Площадь
трапеции равна произведению полусуммы ее оснований на высоту:
S = 0,5 h (a + b)
5. Площадь трапеции равна произведению средней линии на высоту:
S = m h
A
B
C
D