полученное при вращении прямоугольника вокруг оси, проходящей через одну
из его сторон.Определение и общие свойства цилиндра.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

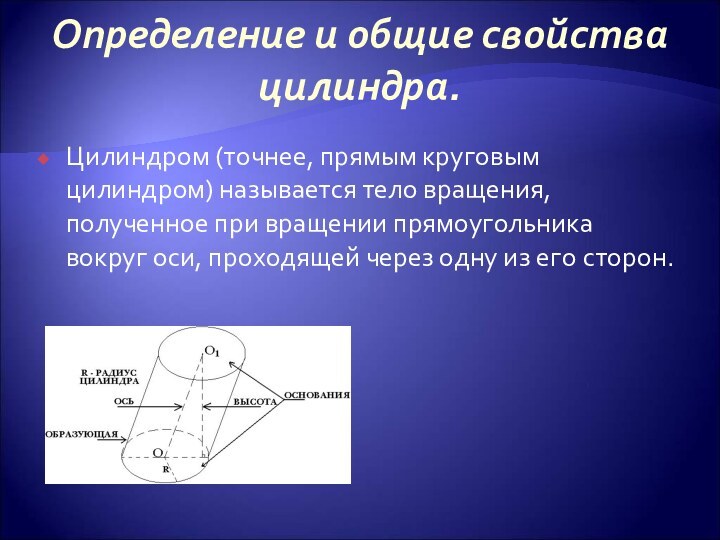










Определение и общие свойства цилиндра.
а) Дано:
ВД = 20см
АВСД – осевое сечение, квадрат.
Цилиндр
Найти:
h - ?;
Решение:
а) Так как АВСД – квадрат, то
АВ=АД. Из треугольника АВД
по теореме Пифагора: АС2 =
ВА2 + АД; 202 = h2 + h2; 202 = 2h2; h
400 = 2 h2; h2 = 400; h = 10√2 .