Презентация на тему по геометрии на тему: Сечение многогранников (10 класс)

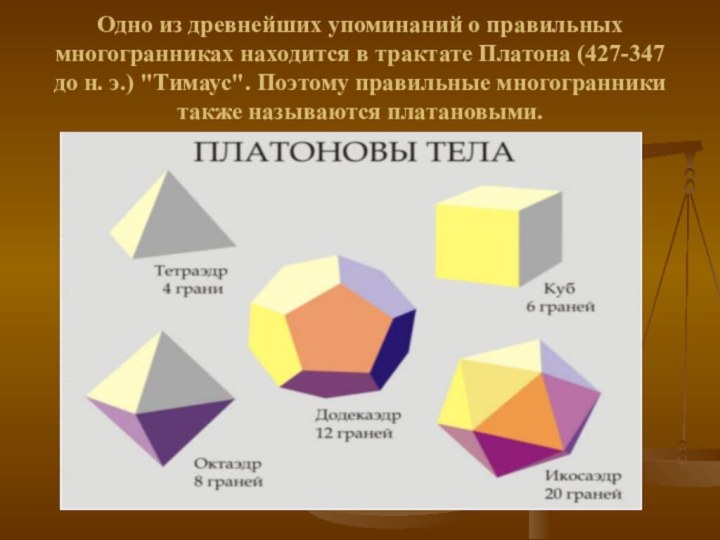
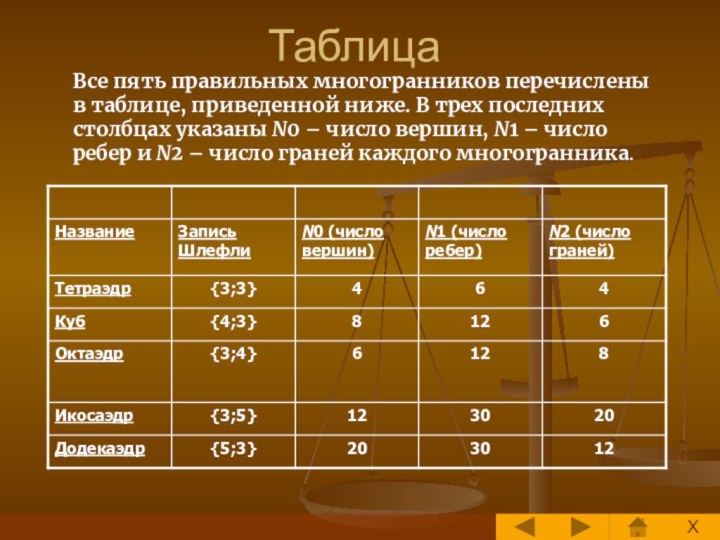
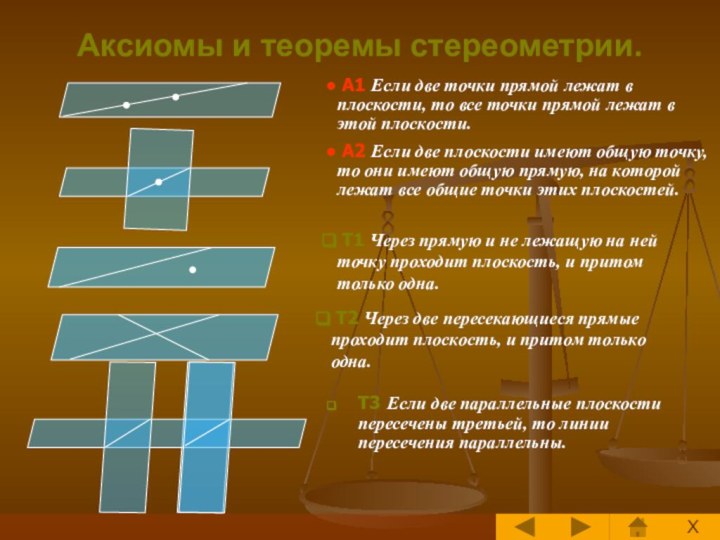
стереометрии
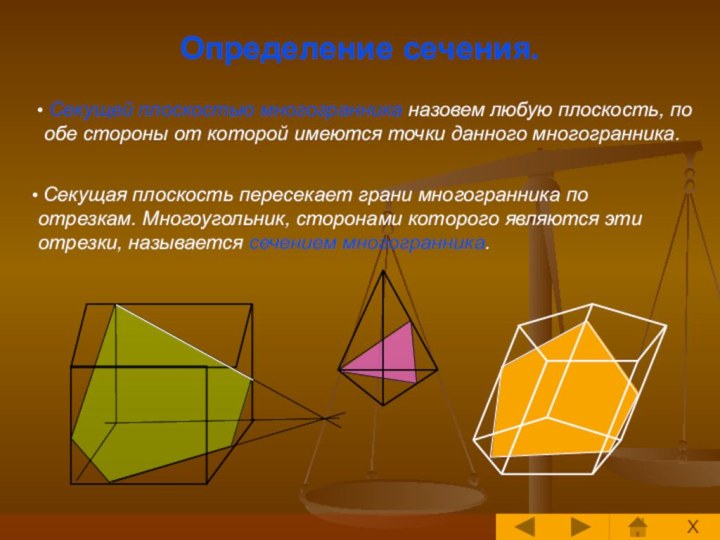
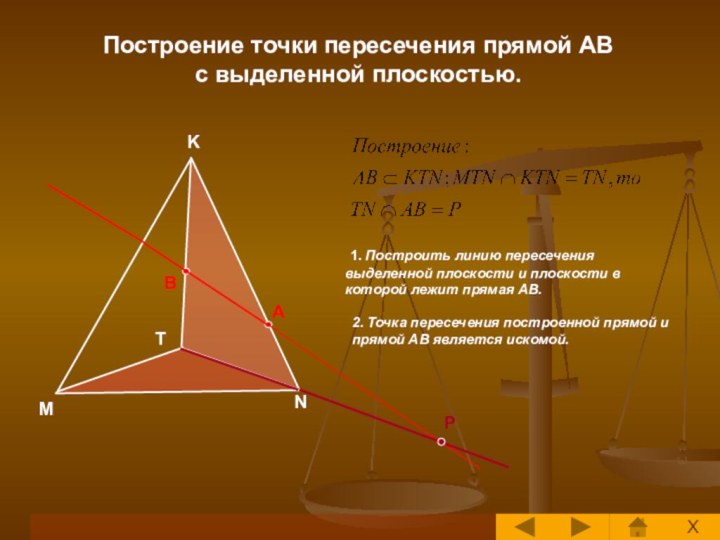
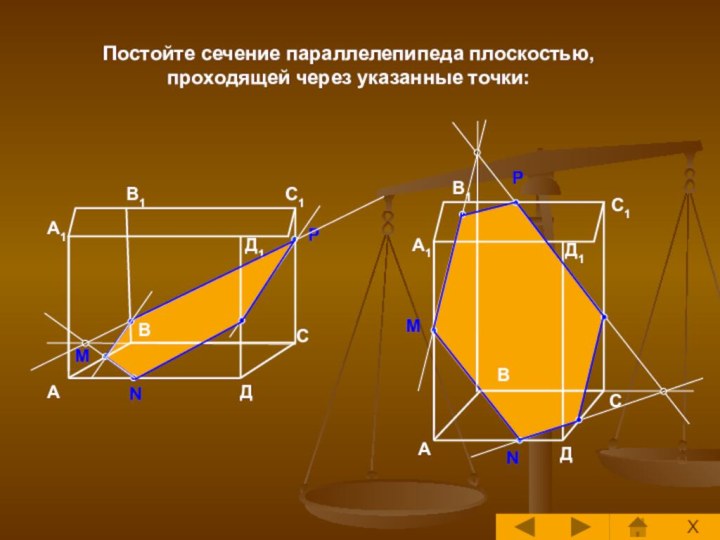
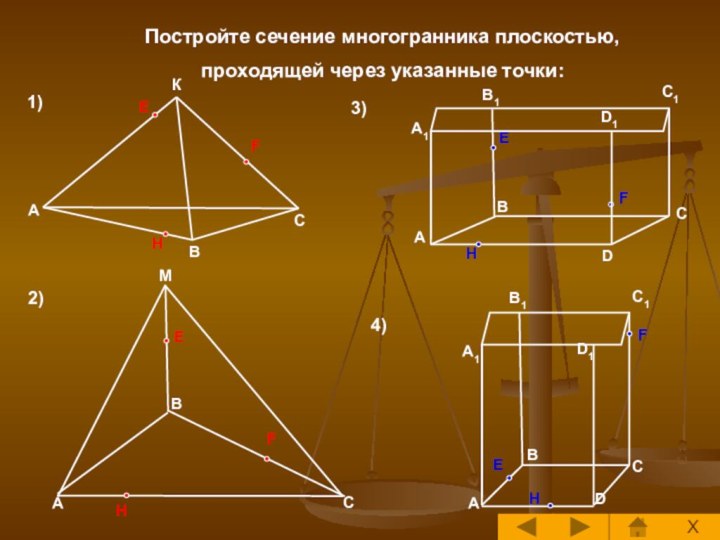
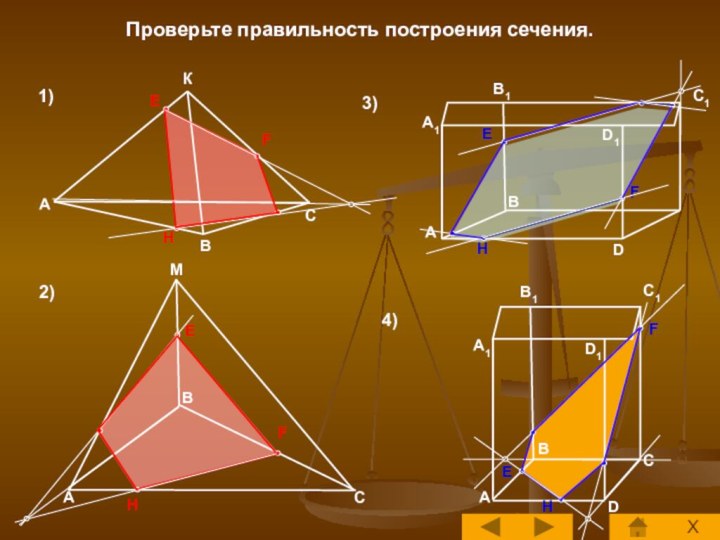
Построение сечений многогранника
Многогранники в архитектуре
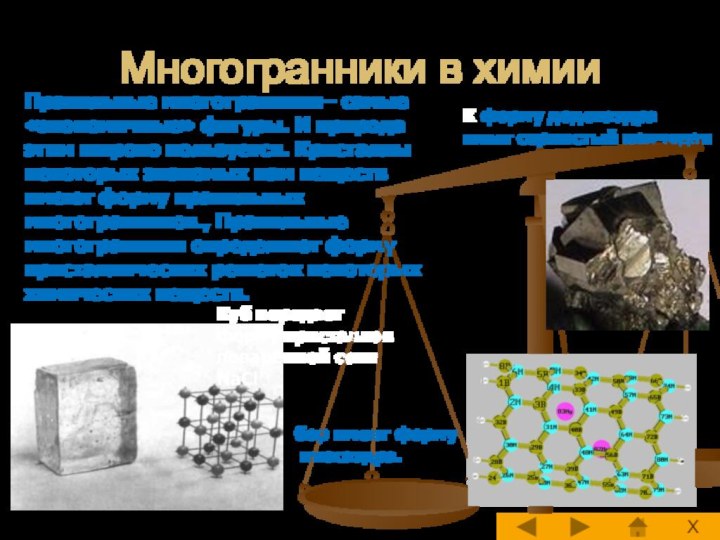
Многогранники в химии
Многогранники

в биологии
Использованная литература

X

в трактате Платона (427-347 до н. э.) "Тимаус". Поэтому

правильные многогранники также называются платановыми.

приведенной ниже. В трех последних столбцах указаны N0 –

число вершин, N1 – число ребер и N2 – число граней каждого многогранника.

Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма

плоских углов при каждой вершине равна 270 °.

X

треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно

сумма плоских углов при каждой вершине равна 180°.

X

Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно сумма

плоских углов при каждой вершине равна 240°.

X

треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно

сумма плоских углов при каждой вершине равна 300 °.

X

пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.

Следовательно, сумма плоских углов при каждой вершине равна 324°.

X

которого (основания призмы) представляют собой равные многоугольники с взаимно

параллельными сторонами, а все другие грани параллелограммы.

Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом

X

расположенными в параллельных плоскостях (они являются его основаниями); его

боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований

X

многоугольник, а остальные грани - треугольники с общей вершиной.

Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью.

X

по обе стороны от которой имеются точки данного многогранника.

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

X

пересечены третьей, то линии пересечения параллельны.


















X
А1 Если

две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

А2 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Т1 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Т2 Через две пересекающиеся прямые проходит плоскость, и притом только одна.

1. Построить линию пересечения выделенной плоскости и плоскости в

которой лежит прямая АВ.

2. Точка пересечения построенной прямой и прямой АВ является искомой.

N

Р

X

широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму

правильных многогранников., Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.

Многогранники в химии

Куб передает форму кристаллов поваренной соли NaCl

К форму додекаэдра
имеет сернистый колчедан

бор имеет форму
икосаэдра.

X

в центре внимания биологов в их спорах относительно формы

вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр. Его геометрические свойства помогают экономить генетическую информацию.

X

параллельны, расстояние между ними выдерживается с удивительным постоянством. Пчелиные

ячейки представляют собой шестигранные геометрические фигуры.

X