- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора 9 класс
Содержание
- 2. Из историиУченый Пифагор родился около 570 г.
- 3. ТеоремаВ прямоугольном треугольнике квадрат гипотенузы равен сумме
- 4. Доказательство теоремыДано: а,b-катеты,с-гипотенуза. Доказать:a2+b2=c2.Доказательство:Достроим до квадрата со стороной (a+b).S1=(a+b)2S2=4(1/2ab)+c2Приравняем площади:S1=S2.(a+b)2=4(1/2ab)+c2а2+2ab+b2=2ab+c2а2+b2=c2
- 5. Музыка и ПифагорСначала Пифагор занялся музыкой. Занимаясь
- 6. Покрытие плоскости Занимаясь вопросом о покрытии плоскости правильными
- 7. Чем были числа для Пифагора? Пифагор стал
- 8. Пифагор провозгласил, что числа правят миром, и
- 9. Делимость чисел Изучая свойства чисел, пифагорейцы первые обратили
- 10. Совершенные числаПифагорейцы занимались задачей о нахождении совершенных
- 11. Содружественные числаДва числа, обладающие тем свойством, что
- 12. Космос и Пифагор Пифагорейство предполагает существование десяти "принципов",
- 13. Пифагоровы числа «…Именно наука о числе может
- 14. ЗадачаВот задача индийского математика 12 в. Бхаскары На
- 15. ЗадачаСлучися некоему человеку к стене лествицу прибрати,
- 16. Это интересноТеорема Пифагора считалась у учащихся средних
- 17. Афоризмы "Не ешь недолжного, а именно ни рождения,
- 18. Применение теоремыРассмотрим примеры практического применения теоремы Пифагора.
- 19. Диагональ d квадрата со стороной а можно
- 20. Высота h равностороннего треугольника со стороной а
- 22. Значение теоремы
- 23. Скачать презентацию
- 24. Похожие презентации
Из историиУченый Пифагор родился около 570 г. до н.э. На острове Самосе. По античным свидетельствам он был красив и обладал незаурядными способностями. В 548 г. до н.э. он прибыл в Навкратис. Научившись всему, что






















Слайд 3
Теорема
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
его катетов:
c2 = a2 + b2
Как додумался Пифагор до
этого утверждения, никаких сведений нет. Возможно, он начертил прутиком на песке, ведь пифагорейцы часто гуляли и на прогулках занимались наукой. Согласно легенде, в знак благодарности он принес богам в жертву 100 быков. И в легендах говорится, что, когда открывается что-то новое, вся скотина на земле дрожит от страха. Возможно, Пифагор собрал всех математиков и рассказал о своем открытии. Об этом повествует одна из глиняных табличек. В ней есть только задачи, а никаких выводов нет.
Но в индийских рукописях сохранился чертеж и слово "теорема", которое происходит от греческого слова "теорио" - рассматриваю.
Слайд 4
Доказательство теоремы
Дано: а,b-катеты,с-гипотенуза. Доказать:a2+b2=c2.
Доказательство:
Достроим до квадрата со стороной
(a+b).
S1=(a+b)2
S2=4(1/2ab)+c2
Приравняем площади:S1=S2.
(a+b)2=4(1/2ab)+c2
а2+2ab+b2=2ab+c2
а2+b2=c2
Слайд 5
Музыка и Пифагор
Сначала Пифагор занялся музыкой. Занимаясь гармонией,
пифагорейцы пришли к выводу, что качественные отличия звуков обуславливаются
чисто количественными различиями длин струн или флейт. Так, гармонический аккорд при звучании трех струн получается в том случае, когда длины этих струн сопоставляются с соотношением чисел 3, 4 и 6. Такое же соотношение было подмечено пифагорейцами и во многих других случаях. Например, отношение числа граней, вершин и ребер куба равно отношению чисел 6:8:12.И тогда Пифагор решил, что не только законы музыки, но и вообще все на свете можно выразить с помощью чисел. "Числа правят миром"! - провозгласил он.
Слайд 6
Покрытие плоскости
Занимаясь вопросом о покрытии плоскости правильными одноименными
многоугольниками, пифагорейцы нашли, что возможны только три случая таких
покрытий: вокруг одной точки плоскости можно плотно уложить или шесть правильных треугольников, или четыре правильных четырехугольника (квадрата), или же три правильных шестиугольника. Если обратим внимание на числа правильных многоугольников в этих трех случаях, то увидим, что их отношение равно отношению 6:4:3, если же возьмем отношение числа сторон этих многоугольников, то найдем, что оно равно отношению чисел 3:4:6. На основе подобных наблюдений в школе Пифагора возникло убеждение, что во всей Вселенной явления подчинены вполне определенным числовым соотношениям, то есть существует "мировая гармония", что "элементы чисел являются элементами всех вещей и что весь мир в целом является гармонией и числом". Если обратим внимание на числа правильных многоугольников в этих трех случаях, то увидим, что их отношение равно отношению 6:4:3, если же возьмем отношение числа сторон этих многоугольников, то найдем, что оно равно отношению чисел 3:4:6. На основе подобных наблюдений в школе Пифагора возникло убеждение, что во всей Вселенной явления подчинены вполне определенным числовым соотношениям, то есть существует "мировая гармония", что "элементы чисел являются элементами всех вещей и что весь мир в целом является гармонией и числом".
Слайд 7
Чем были числа для Пифагора?
Пифагор стал думать о
свойствах четных и нечетных чисел. Но во времена Пифагора
на человека, сказавшего, что неизвестное число можно обозначить буквой, посмотрели бы с удивлением. И Пифагор начал изображать числа точками. Мы изображаем четные числа в виде 2п, а нечетные - 2П+1. Чтобы доказать, что произведение двух нечетных чисел нечетно, он строил из точек прямоугольник. Потом Пифагор стал усложнять свои фигуры из точек. Вместо прямоугольника он стал строить треугольник. Они получили имя треугольных (1,3,6,10,15,21). Затем он стал строить квадраты (1,4,9,16). Такие числа получили название квадратных. Пифагор из точек стал складывать пирамиды, кубы, изучать пирамидальные, кубические и иные числа.
Слайд 8
Пифагор провозгласил, что числа правят миром, и поэтому
он придумывал, как с помощью чисел изображать такие понятия,
как справедливость, совершенство, дружба. Справедливость символизировало число 4. Четные числа Пифагор считал женскими, а нечетные - мужскими. Бракосочетание он обозначал числом 5, 3+2=5 (четное + нечетное). Первыми четырьмя числами - 1,2,3,4 он обозначал четыре элемента, из которых, по воззрениям древнегреческих мудрецов, состоял весь мир: 1 - огонь, 2 - земля, 3 - вода, 4 - воздух. 1+2+3+4=10. Число 10 вбирает в себя весь мир. Он очень чтил число 7, приписывал ему важную роль в небесных делах. 12 - знак счастья, "666"- "число зверя". У пифагорейцев существовала клятва числом 36. 36 = 13 + 23 + 33 36 = (2+4+6+8) + (1+3+5+7). Число 1 - матерь всех чисел, число 1 есть точка. Число 2 выражало линию. Число 3 - треугольник, треугольник задает плоскость. Число 4 - пирамида, трехмерный образ. Пифагорейцы связывали арифметику с геометрией. Они глубоко верили в чудесные свойства числа 10. Пифагорейцы сформулировали теорему: произведение 2 чисел делится на два только тогда, когда по крайней мере один из сомножителей делится на 2. Пифагорейцы нашли дружественные, или совершенные, числа. Совершенные числа - это такие, которые равны сумме своих делителей (исключая само число). 6 = 1+2+3, 28 = 1+2+4+7+14.
Слайд 9
Делимость чисел
Изучая свойства чисел, пифагорейцы первые обратили внимание
на законы их делимости. Они разбили все числа на
четные – "мужские", и нечетные – "женские", или, иначе, "гномоны" и, что очень важно, на простые и составные. Пифагорейцы называли составные числа, представляемые в виде произведения двух сомножителей, "плоскими числами" и изображали их в виде прямоугольников, а составные числа, представляемые в виде произведения трех сомножителей, – "телесными числами" и изображали их в виде параллелепипедов. Простые числа, которые нельзя представить в виде произведений, они называли "линейными числами". Пифагорейцы создали так называемое учение о четных и нечетных числах, которое с современной точки зрения является теорией делимости на 2.
Слайд 10
Совершенные числа
Пифагорейцы занимались задачей о нахождении совершенных чисел,
то есть таких, которые равны сумме своих делителей (исключая
само число), как, например, 6=1+2+3 или 28=1+2+4+7+14. Совершенных чисел не много. Среди однозначных – это только 6, среди двузначных, трехзначных и четырехзначных – только 28, 496 и 8128 соответственно.Однако вопрос о том, имеется ли конечное или бесконечное число совершенных чисел, до сих пор не решен, также не найдено ни одного нечетного совершенного числа и не доказано, что таких чисел не существует.
Слайд 11
Содружественные числа
Два числа, обладающие тем свойством, что сумма
делителей каждого из них равняется другому, назывались "содружественными". Как
утверждают, Пифагор на вопрос, что такое друг, ответил: "Тот, кто есть другой я, вот как числа 220 и 284". При помощи компьютера в одном из университетов США были исследованы все числа до миллиона. В результате были получены 42 пары содружественных чисел:220 284 1184 1210 2620 2924 5020 5564 6232 6368 и т. д. Существуют и пары нечетных содружественных чисел:
12285 14595 67095 87633 и др. Однако общая формула для этих чисел не найдена, мало известно и об их свойствах.
Слайд 12
Космос и Пифагор
Пифагорейство предполагает существование десяти "принципов", порождающих
космос. Космос (понятие, введенное пифагорейцами) – это гармония, тетрактис,
совершенство, порядок, мера. Вселенная, созданная числом и противоположными принципами (конечность – бесконечность), ведет себя логически, соразмерно необходимости и меры. Первые из них положительные, вторые – отрицательные. В каждом числе Пифагор определял тот или иной принцип, закон, ту или иную активную силу. Противоположность между нечетными (высшими) и четными (низшими, порожденными из высших путем удвоения) числами проявляется в природе в виде ряда других противоположностей: свет и тьма, безграничное и ограниченное, доброе и злое, движущееся и покоящееся, мужское и женское и т. д. Естественный мир реально построен из чисел: тело ограничено плоскостями, плоскость – линиями, линия – точками. Точка – последний элемент Вселенной – тождественна единице. Т. о. возникает соответствие между пространственным миром и числами: линия – "2", плоскость – "3", тело – "4". К числу сводится и мир духа: любовь и дружба отождествляются с восьмеркой, справедливость – с кратными числами.
Слайд 13
Пифагоровы числа
«…Именно наука о числе может обладать ключом
жизни и сути бытия…»
«…Так, четные числа делятся на сверх
совершенные (сумма дробных частей, которых больше их самих –24 имеет суммой дробных частей 12+6+4+8+3+2+1=33, 33 больше24), несовершенные (сумма дробных частей, которых меньше его самого – 14 сумма его дробных частей 7+2+1=10, 10 меньше14) и совершенные (сумма дробных частей которого равна самому числу – 28, 496, 8128)…»Тройки чисел, удовлетворяющих уравнению c2=a2+b2, называют пифагоровыми (5,12,13 и 7,24,25).
Слайд 14
Задача
Вот задача индийского математика 12 в. Бхаскары
На берегу
реки рос тополь одинокий. Вдруг ветра порыв его ствол
надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
Слайд 15
Задача
Случися некоему человеку
к стене лествицу прибрати,
стены
тоя же высота есть 117 стоп. И обрете лествицу
долготою 125 стоп. И ведати хощет, колико стоп сея лествици нижний конец
от стены отстояти имать.
Слайд 16
Это интересно
Теорема Пифагора считалась у учащихся средних веков
очень трудной и называлась иногда- ослиный мост или- бегство
убогих, т. к . некоторые "убогие" ученики, не имевшие серьезной подготовки, бежали от геометрии. Слабые ученики, заучившие теорему наизусть без понимания и прозванные поэтому "ослами", не были в состоянии преодолеть теорему Пифагора, служившую для них вроде непроходимого моста . Теорему Пифагора учащихся называли так же "ветряной мельницей"
Слайд 17
Афоризмы
"Не ешь недолжного, а именно ни рождения, ни
приращения, ни начала, ни завершения, ни того, в чем
первооснова всего” Не разрушай жизненные основы и не подрывай сил природы, рожденье, рост, становление. "Огня ножом не вороши“ – Не трогай первоэлементы, ибо огнь есть пирамида, первый знак духовности. "Не ешь сердца" – Не ничтожь счастье других и не терзай себя душевными муками. "Не садись на хлебную меру“ – С равным достоинством относись к малым и великим мира сего. "Через весы не шагай“ – Не нарушай равновесия в природе. "Венка не обрывай“ – Хвалу и хулу бессмертным не воздавай, не покушайся на вечность.
Слайд 18
Применение теоремы
Рассмотрим примеры практического применения теоремы Пифагора. Не
будем пытаться привести все примеры использования теоремы - это
вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости :
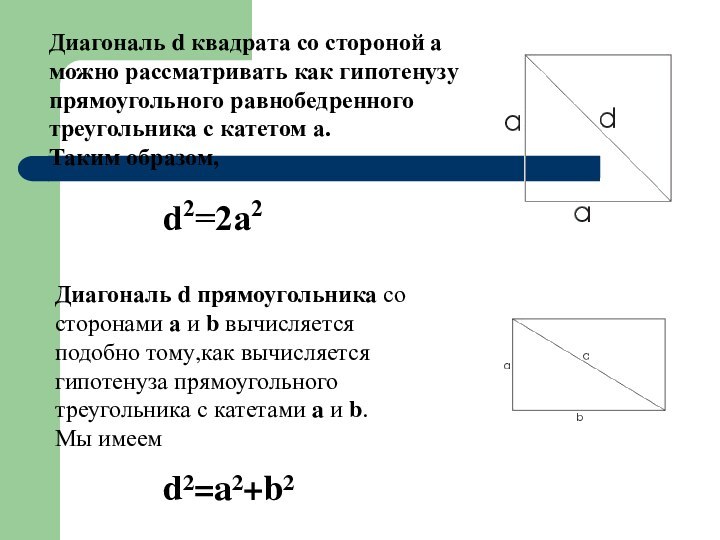
Слайд 19 Диагональ d квадрата со стороной а можно рассматривать
как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b.
Мы имеем
d²=a²+b²
d2=2a2
Слайд 20 Высота h равностороннего треугольника со стороной а может
рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а
другой катет а/2. Таким образомh2=a2+(a/2)2; h2=3a2/4; h=?