- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора доказательство
Содержание
- 2. Золотая теорема геометрииКвадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.Елекова Э.М. Республика Алтай
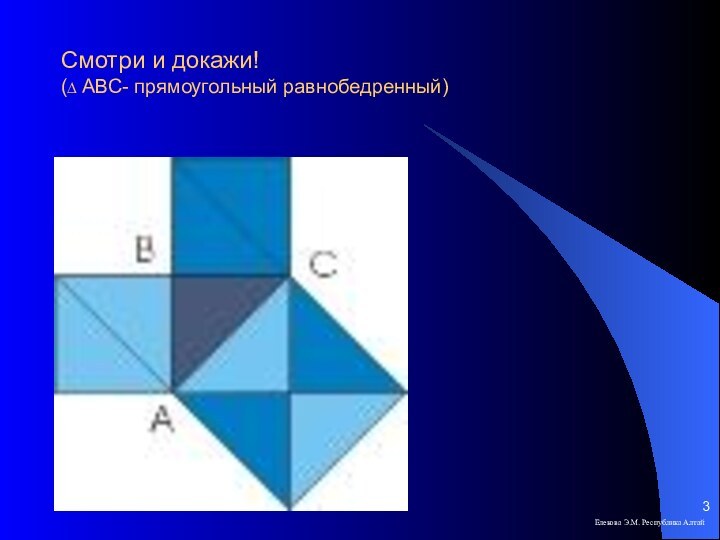
- 3. Смотри и докажи! (∆ АВС- прямоугольный равнобедренный)Елекова Э.М. Республика Алтай
- 4. Смотри и докажи!Елекова Э.М. Республика Алтай
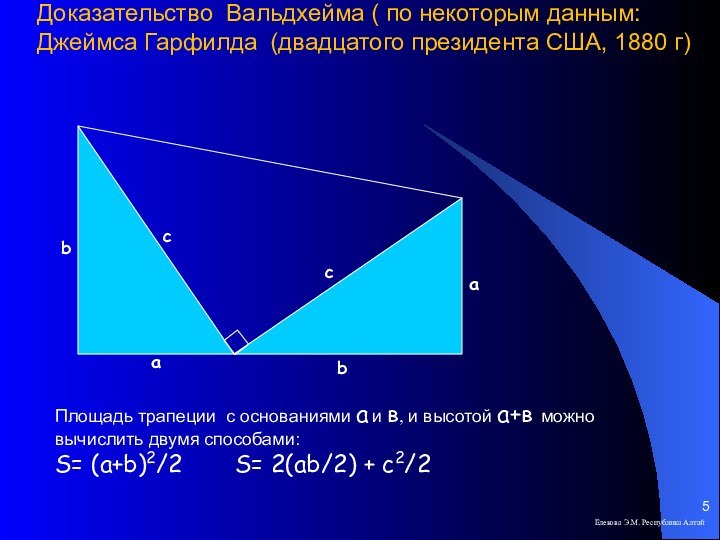
- 5. Доказательство Вальдхейма ( по некоторым данным:
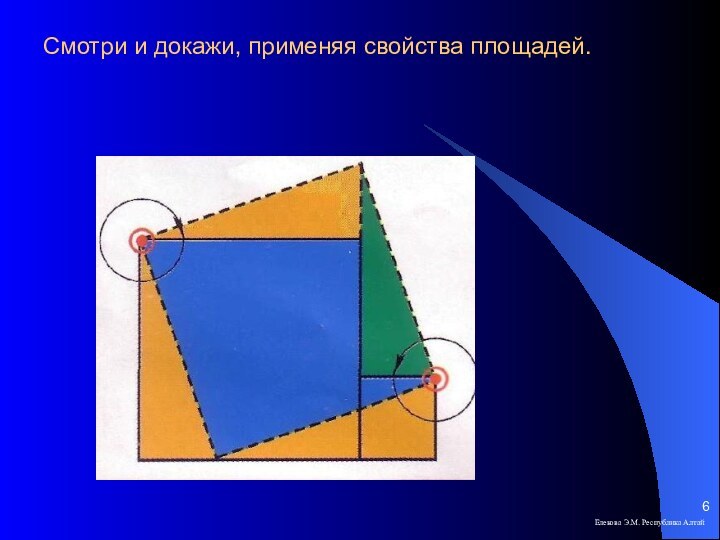
- 6. Смотри и докажи, применяя свойства площадей.Елекова Э.М. Республика Алтай
- 7. Доказательство индийского математика БасхарыЕлекова Э.М. Республика
- 8. Отложим точно такие же треугольники как показано на рисунке.Елекова Э.М. Республика Алтай
- 9. На рисунке есть квадрат, площадь которого
- 10. Квадрат со стороной с состоит из четырех
- 11. Рассуждения:Большой квадрат состоит из четырех равных прямоугольных
- 12. Елекова Э.М. Республика АлтайПовернем треугольник АВС вокруг С на 900 Доказательство Хоукинса
- 13. Елекова Э.М. Республика АлтайS САА1 = b2/2S
- 14. Скачать презентацию
- 15. Похожие презентации
Золотая теорема геометрииКвадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.Елекова Э.М. Республика Алтай







Слайд 2
Золотая теорема геометрии
Квадрат гипотенузы прямоугольного треугольника равен сумме
квадратов его катетов.
Слайд 5 Доказательство Вальдхейма ( по некоторым данным: Джеймса Гарфилда
(двадцатого президента США, 1880 г)
Елекова Э.М. Республика Алтай
Площадь трапеции
с основаниями а и в, и высотой а+в можно вычислить двумя способами:S= (a+b)2/2 S= 2(ab/2) + c2/2
Слайд 7
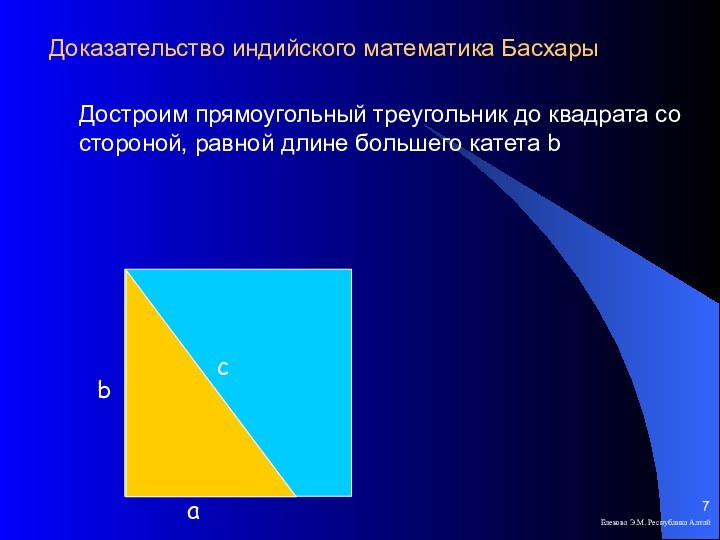
Доказательство индийского математика Басхары
Елекова Э.М. Республика Алтай
a
b
c
Достроим прямоугольный
треугольник до квадрата со стороной, равной длине большего катета
b
Слайд 9
На рисунке есть квадрат, площадь которого равна
b2
Есть квадрат, площадь которого равна c2
Елекова Э.М. Республика Алтай
Слайд 10
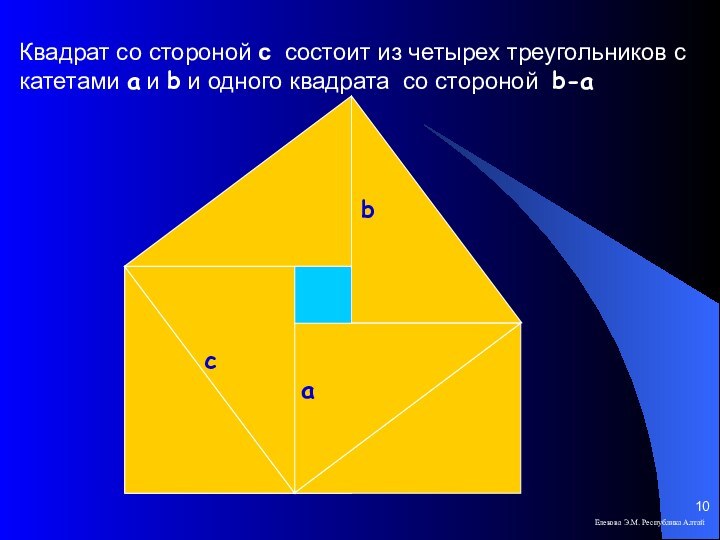
Квадрат со стороной с состоит из четырех треугольников
с катетами a и b и одного квадрата со
стороной b-aЕлекова Э.М. Республика Алтай
a
b
с
Слайд 11
Рассуждения:
Большой квадрат состоит из четырех равных прямоугольных треугольников
с катетами а и b и одного квадрата со
стороной b-aт.е. с2=4∙Sтр + (b-a)2=
= 4∙(ab/2) + (b-a)2= 2ab + b2 - 2ab + a2 =
= a2 + b2
Итак, с2 = a2 + b2 что и требовалось доказать.
Елекова Э.М. Республика Алтай
Слайд 12
Елекова Э.М. Республика Алтай
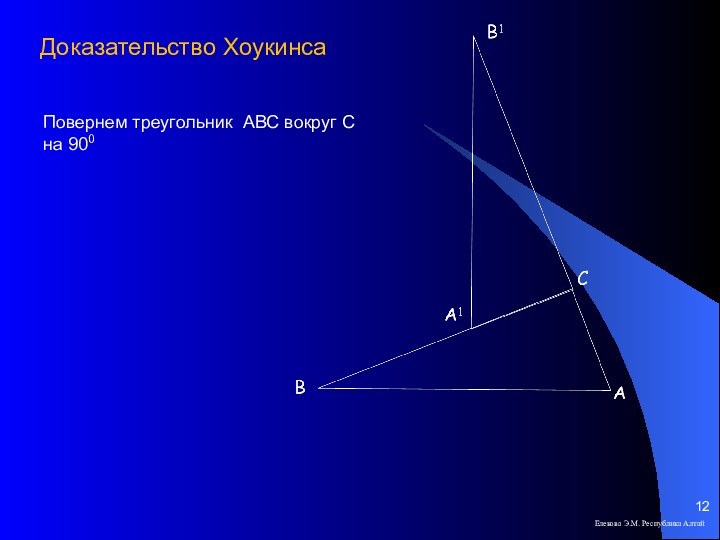
Повернем треугольник АВС вокруг С
на 900
Доказательство Хоукинса
Слайд 13
Елекова Э.М. Республика Алтай
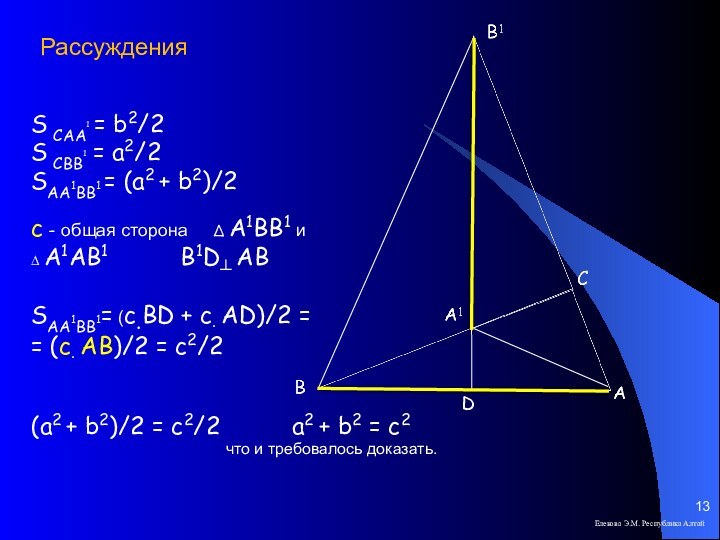
S САА1 = b2/2
S СВВ1
= a2/2
SAA1BB1 = (a2 + b2)/2
с - общая сторона
∆ А1ВВ1 и ∆ А1АВ1 B1D┴ ABSAA1BB1= (c∙BD + c∙ AD)/2 =
= (c∙ AB)/2 = c2/2
(a2 + b2)/2 = c2/2 a2 + b2 = c2
что и требовалось доказать.
Рассуждения