Презентация на тему Параллелограмм Вариньона

(1688).Родился в Каенне. Изучал философию и математику. С 1688-профессор

математики в Коллеже Мазарини, с 1704-Коллеж де Франс.

Вариньон Пьер

и статике. Исходя из теории сложных движений сформулировал

(ок. 1710) закон параллелограмма сил. Развил понятие момента сил и предложил геометрическое доказательство теоремы о том, что момент равнодействующей двух сходящихся сил равен сумме моментов составляющих сил (теорема Вариньона).Установил (1687) теорему о скользящих векторах для случая сходящейся системы сил. Одним из первых начал пользоваться математическим анализом. Изучал равновесие и движение жидкости. Дал объяснение закона Торричелли. Полагая, что вес колонны воды пропорционален высоте h, нашёл выражение для закона Торричелли.

определение четырёхугольника Вариньона.

Доказали свойство: «четырёхугольник Вариньона является параллелограммом».

Определили

вид параллелограмма Вариньона для различных видов четырёхугольников.

для правильного многоугольника также является правильным.

Заключение. Подобрали 7 задач,

в которых использовали теоретический материал работы.

серединах сторон данного четырёхугольника.

Свойство площади параллелограмма Вариньона
теорема:

площадь параллелограмма Вариньона равна половине площади данного четырёхугольника.

ABCD, s-площадь четырехугольника KLMN , вершины которого- K, L,

M, и N середины сторон AB, BC, CD и AD соответственно.
Поскольку KL и MN- средние линии треугольников ABC и ADC, то
S▲DLK=1/4 S▲ADC; S▲BMN=1/4 ▲ABC,
Поэтому:
S▲DLK+S▲BMN=1/4S▲ABC+1/4S▲ADC=
=1/4(S▲ABC +S▲ADC)=1/4S
Аналогично:
S▲KNC+S▲MAL=1/4 S
Следовательно, s=S-S▲DLK-S▲MBN-S▲LAM-S▲NCK=S-1/4S-1/4S=1/2S

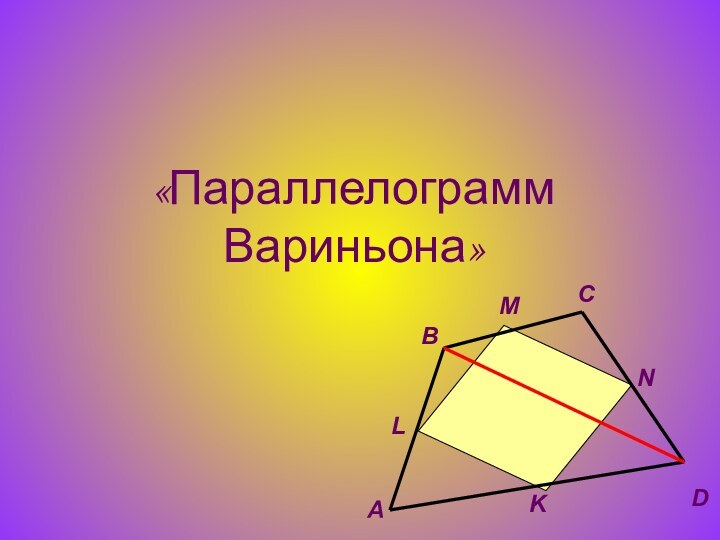
A

B

M

L

D

K

C

N

получим, что EL║BD, и EL=1/2BD 2. Аналогично, рассматривая ▲BCD

получим, что FK║BD, FK=1/2 BD То есть EL=FK; EL║FK, значит четырёхугольник EFKL является параллелограммом, так как две противолежащие стороны четырёхугольника равны и параллельны. А так как диагонали ромба пересекаются под прямым углом, то и параллельные им стороны четырёхугольника будут тоже пересекаться под прямым углом. Следовательно, если исходной фигурой является ромб, то параллелограмм Вариньона принимает вид прямоугольника.

А

В

С

D

E

F

K

L

Определим вид параллелограмма Вариньона для ромба

прямоугольника
Для равнобокой трапеции
Для квадрата

теоретический материал нашей исследовательской работы.

задач:
ABCD- прямоугольник, M, K, P и T- середины его

сторон, AB=6см, AD=12см.
Найти площадь четырехугольника MKPT.
Решение:
MKPT является параллелограммом Вариньона.
Используя свойство площади параллелограмма Вариньона: площадь параллелограмма Вариньона равна половине площади данного четырехугольника, получим:
Площадь MKPT=1/2 площади ABCD => S=1/2 • 6•12=36(кв.см)
Ответ: 36(кв.см)

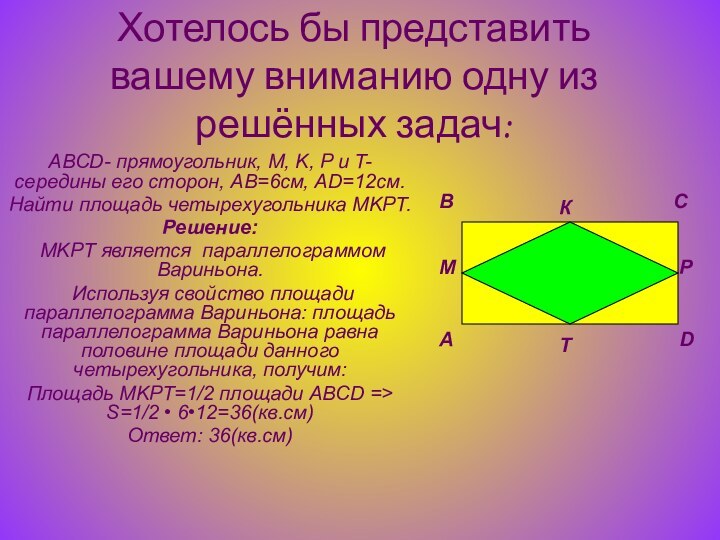
А

В

С

D

М

К

Р

Т

о параллелограмме Вариньона, и нашли их широкое практическое применение

при решении задач.
Эти знания позволили нам более глубоко познакомиться с данным материалом, и применять их в нестандартных ситуациях. Поиск новой информации из различных печатных источников, а так же из сети Интернет расширил наши знания по предмету геометрии. Мы смогли попробовать себя в новой ситуации, когда знания приобретались нами самостоятельно без помощи учителя, а это в свою очередь позволило нам поверить в себя и в свои возможности.
Намеченный нами план был выполнен, и мы планируем продолжить нашу исследовательскую работу на тему «Дельтоид», где будут использоваться полученные нами знания.