- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проект Мир замечательных кривых 7-9 классы
Содержание
- 2. Основополагающий вопросИспользование работы и презентации на уроках,
- 3. Актуальность В анкетировании участвовало 20 учащихся 6-9 классов
- 4. Знают ли учащиеся нашей школы о
- 5. Выяснить, что знают учащиеся по данной
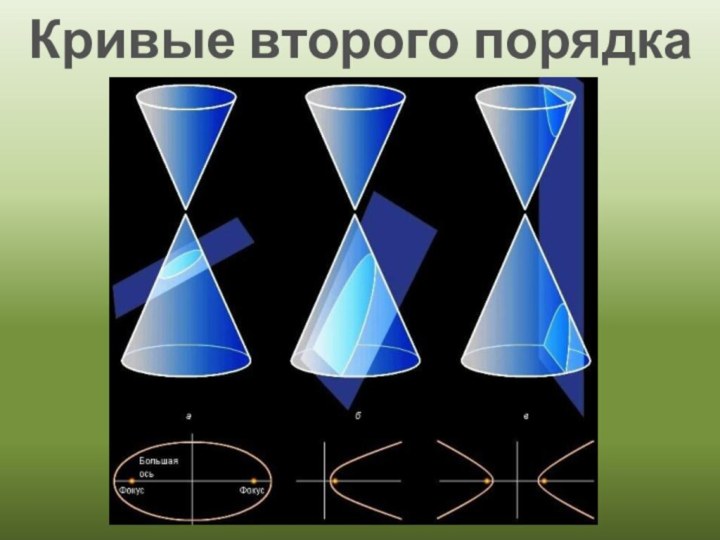
- 6. Кривые второго порядка
- 7. Из истории замечательных кривых Древняя Греция. Менехм
- 8. Из истории замечательных кривых Рене Декарт
- 9. Из истории замечательных кривых
- 10. ПАРАБОЛА
- 11. ПАРАБОЛАГеометрическим местом точек называется фигура, состоящая
- 12. Фокальное свойство параболы
- 13. ЭЛЛИПС
- 14. ЭЛЛИПСЭллипс геометрическое место точек плоскости,
- 15. Оптическое свойство эллипса
- 16. ГИПЕРБОЛАГипербола это геометрическое место точек
- 17. ГИПЕРБОЛА
- 18. ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
- 19. СПИРАЛИ
- 20. Построение спирали Архимеда циркулемПостроение спирали Архимеда с помощью подручных средств
- 21. Спирали в окружающем нас миреСпиралевидная галактикаГалактика вблизи Млечного ПутиТорнадоСмерчОбласть низкого давления над ИсландиейСпиральная галактика Водоворот
- 22. Спирали в мире растений Удивительные формы
- 23. Спираль Архимеда в техникеВинт Архимеда стал
- 24. Спирали в архитектуре Это шпили соборов, винтовые лестницы, элемент декораСпиральные небоскребыпо всему миру
- 25. Построение гипоциклоиды Представим, что по прямой
- 26. Заключение Учащимся полезно знать информацию о
- 27. Скачать презентацию
- 28. Похожие презентации



















Слайд 4
Знают ли учащиеся нашей школы о замечательных кривых
и их свойствах?
Как заинтересовать учащихся изучением кривых второго порядка?
Действительно
ли замечательные кривые и их свойства так широко используются в жизни человека.Проблемные вопросы
Цели проекта
Через практические работы изучить замечательные кривые, их свойства;
Узнать проявления и применение замечательных кривых в окружающем нас мире.
Слайд 5
Выяснить, что знают учащиеся по данной теме;
Собрать материал
по истории, свойствам, построению и применению замечательных кривых;
Изготовить простые
приборы, построить изучаемые кривые и убедиться, что это совсем несложно; Составить компьютерную презентацию по данной теме для применения на уроках математики, занятиях элективных курсов и математического кружка
Задачи проекта
Гипотеза решения проблемы
В помощь учителю. Используя минимум времени, принести максимум пользы.
Слайд 7
Из истории замечательных кривых
Древняя Греция.
Менехм
(около 340 до н.э.) первым изучал замечательные кривые.
Менехм открыл:
эллипс, гипербола и парабола это сечения конусов. Аполлоний Пергский (около 200 лет до н. э.) наиболее полное сочинение «Конические сечения».
Аполлоний дал современные названия кривых – эллипс, парабола и гипербола.
Фокусы эллипса и гиперболы были известны Аполлонию.
Папп Александрийский (вторая
пол. III в.) впервые установил.
фокус параболы.
Слайд 8
Из истории замечательных кривых
Рене Декарт (1596-1650) —
французский философ, математик, механик, физик и физиолог, создатель аналитической
геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.Блез Паска́ль (1623-1662) — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
Пьер де Ферма́ (1601-1665) — французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма.
Слайд 9
Из истории замечательных кривых
Кеплер
открыл из наблюдений, Ньютон теоретически обосновал: планеты и кометы
Солнечной системы движутся по кривым второго порядка, в одном из фокусов которого находится солнце. Орбиты планет — эллипсы, траектории комет — эллипсы, гиперболы или «почти параболы».Ио́ганн Ке́плер (1571-1630) — немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.
Исаа́к Нью́тон (1643-1727) — английский физик, математик, механик и астроном, один из создателей классической физики. В «Математических началах натуральной философии» изложил закон всемирного тяготения и три закона механики.
Слайд 11
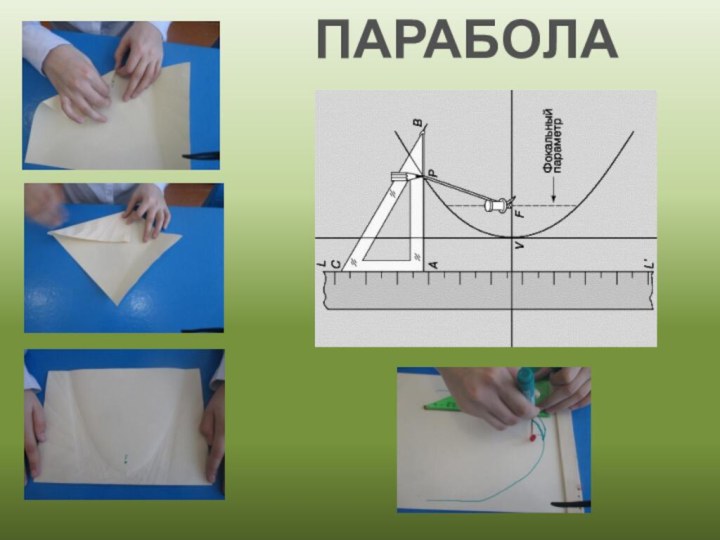
ПАРАБОЛА
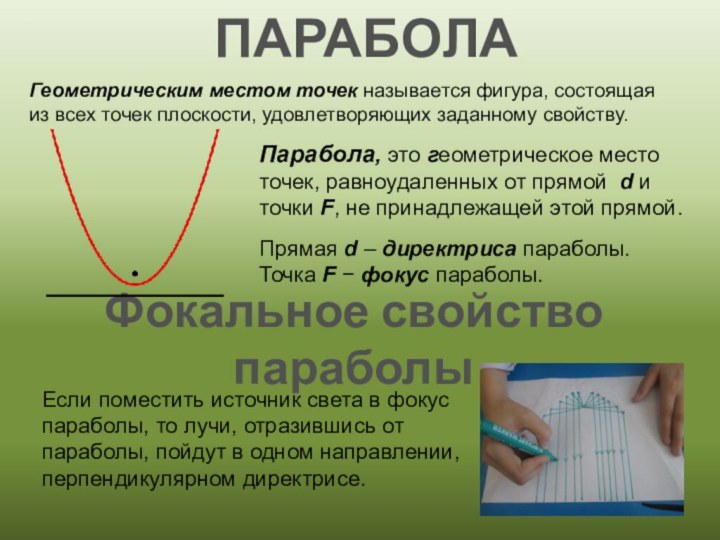
Геометрическим местом точек называется фигура, состоящая
из всех
точек плоскости, удовлетворяющих заданному свойству.
Парабола, это геометрическое место
точек, равноудаленных от прямой d и точки F, не принадлежащей этой прямой.Прямая d – директриса параболы.
Точка F − фокус параболы.
Фокальное свойство параболы
Если поместить источник света в фокус параболы, то лучи, отразившись от
параболы, пойдут в одном направлении, перпендикулярном директрисе.
Слайд 14
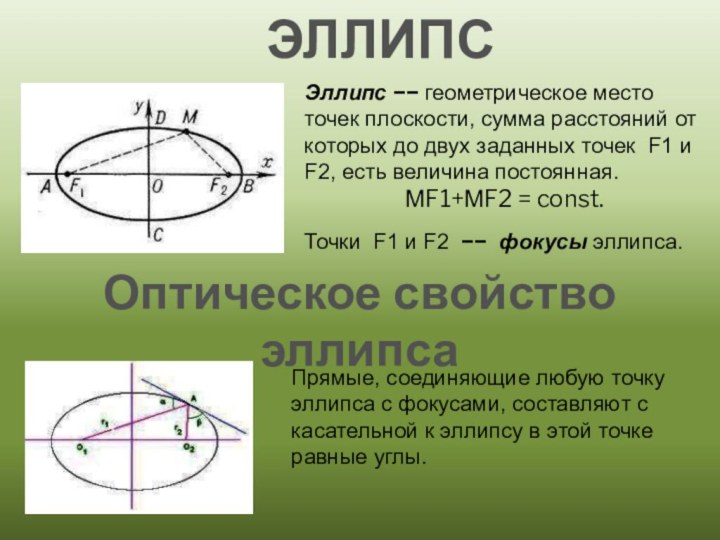
ЭЛЛИПС
Эллипс геометрическое место точек плоскости, сумма расстояний
от которых до двух заданных точек F1 и F2,
есть величина постоянная.МF1+МF2 = const.
Точки F1 и F2 фокусы эллипса.
Оптическое свойство эллипса
Прямые, соединяющие любую точку эллипса с фокусами, составляют с касательной к эллипсу в этой точке равные углы.
Слайд 16
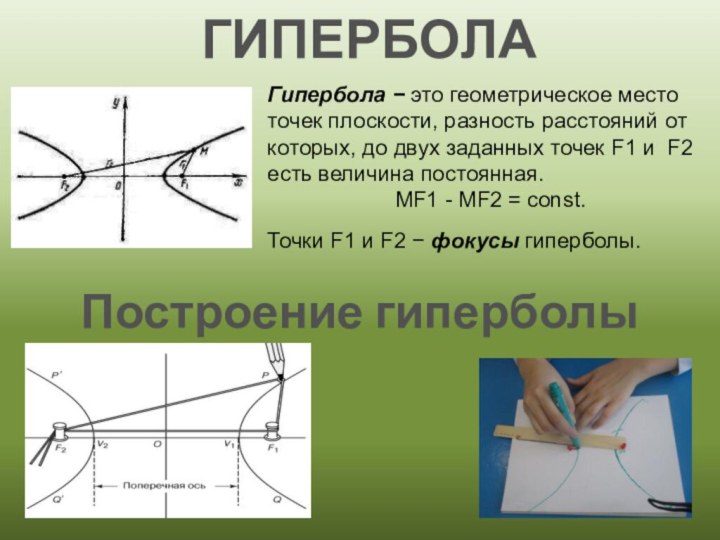
ГИПЕРБОЛА
Гипербола это геометрическое место точек плоскости, разность
расстояний от которых, до двух заданных точек F1 и
F2 есть величина постоянная.МF1 - МF2 = const.
Точки F1 и F2 фокусы гиперболы.
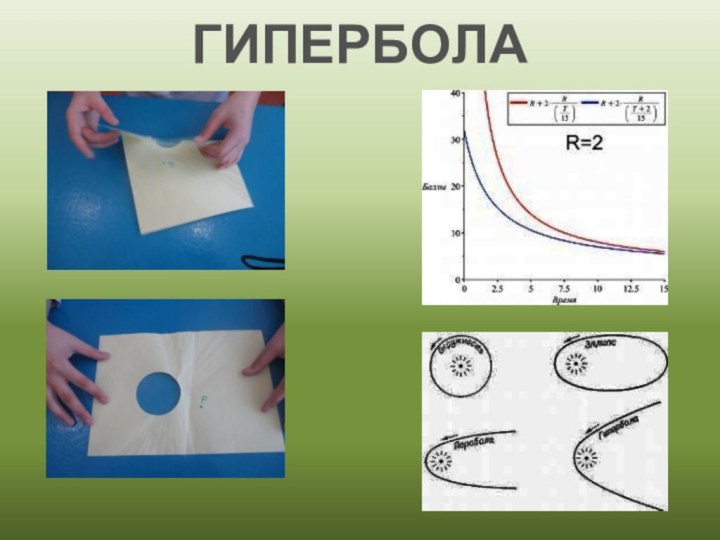
Построение гиперболы
Слайд 19
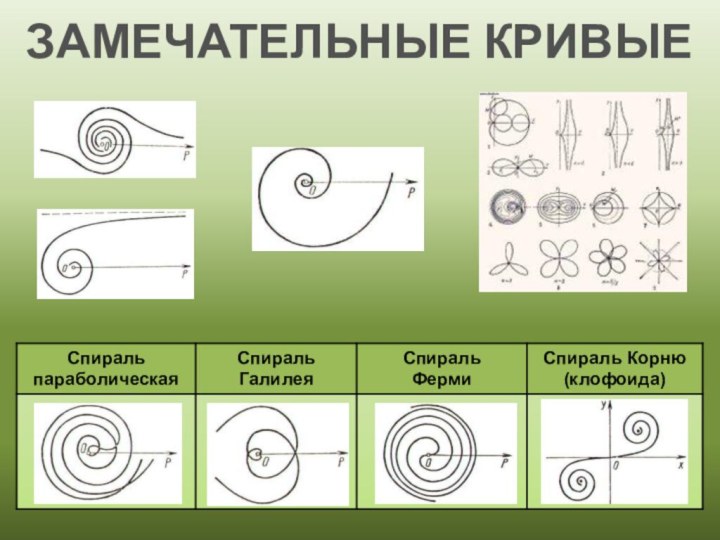
СПИРАЛИ
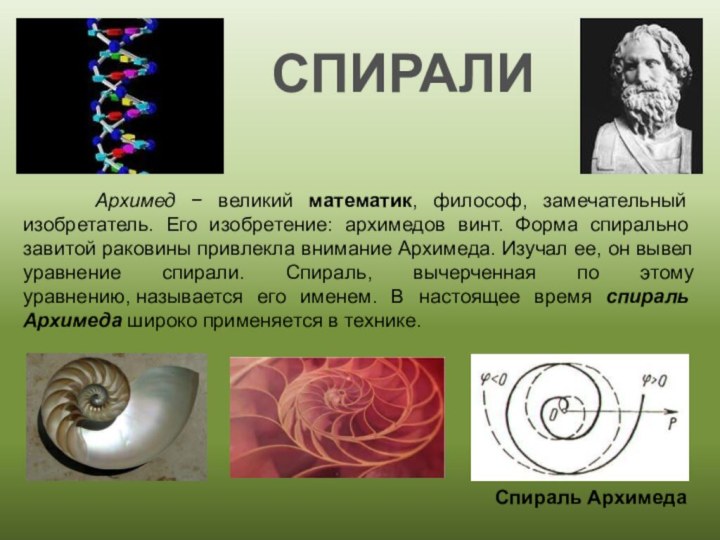
Архимед великий математик, философ, замечательный изобретатель. Его изобретение:
архимедов винт. Форма спирально завитой раковины привлекла внимание Архимеда. Изучал ее, он вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. В настоящее время спираль Архимеда широко применяется в технике.Спираль Архимеда
Слайд 20
Построение спирали Архимеда циркулем
Построение спирали Архимеда с помощью
подручных средств
Слайд 21
Спирали в окружающем нас мире
Спиралевидная галактика
Галактика вблизи Млечного
Пути
Торнадо
Смерч
Область низкого давления над Исландией
Спиральная галактика Водоворот
Слайд 22
Спирали в мире растений
Удивительные формы спиралей кактусов,
алоэ и ананасов
Спирали на сосновой шишке. В крупных
шишках удается разглядеть 5 и 8 и даже 8 и 13 спиралей.Головка цветка подсолнуха как бы соткана из спиралей.
У подсолнуха среднего размера корзинка содержит 34 спирали одного и 55 другого типа
Слайд 23
Спираль Архимеда в технике
Винт Архимеда стал прообразом шнека
- устройства, используемого в машинах для перемешивания жидких, сыпучих
и тестообразных материалов. Самая распространенная разновидность - винтовой ротор в обычной мясорубке
Слайд 24
Спирали в архитектуре
Это шпили соборов, винтовые лестницы,
элемент декора
Спиральные небоскребы
по всему миру
Слайд 25
Построение гипоциклоиды
Представим, что по прямой линии без
скольжения катится круг. Проследим за траекторией, которую опишет при
этом точка А, взятая на окружности этого круга. Начертим получившуюся кривую ЦИКЛОИДУ.
Слайд 26
Заключение
Учащимся полезно знать информацию о кривых, важно
узнать их замечательные свойства.
Изучая свойства кривых, учащиеся видят
действительно практическое применение математики.Собранный материал показывает, как просто построить замечательные кривые.
Работа по замечательным кривым поможет учителям красочно и доступно продемонстрировать учащимся практическое применение свойств замечательных кривых, научить строить кривые при помощи несложных школьных инструментов и подручного материала.
Эта тема интересна и содержательна, развивает познавательный интерес к математике и творческую самостоятельность, открывает практическое применение математики в жизни.





























