двух кругов, не лежащих в одной плоскости и совмещаемых
параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих круговА1
В
А
В1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




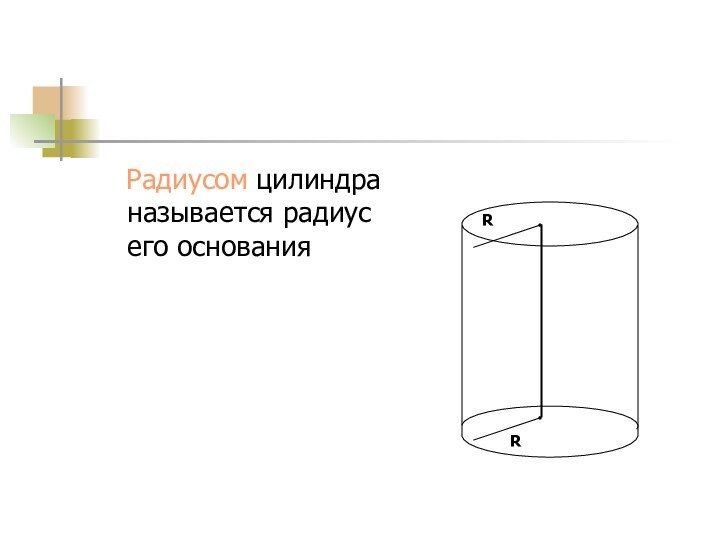




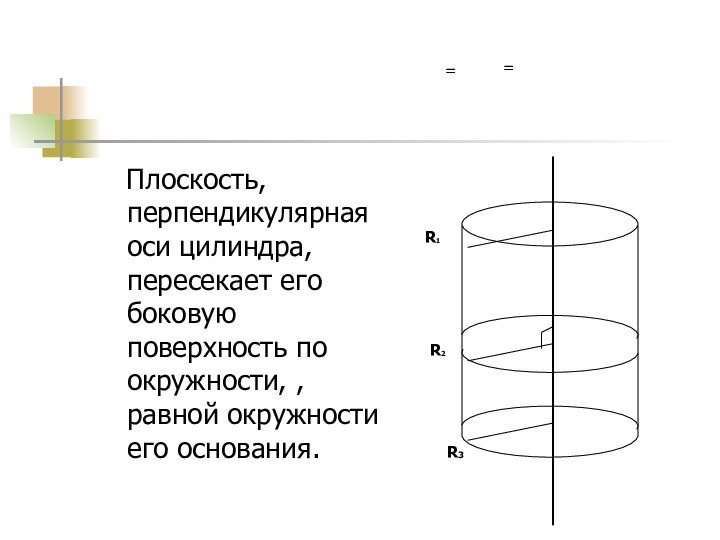


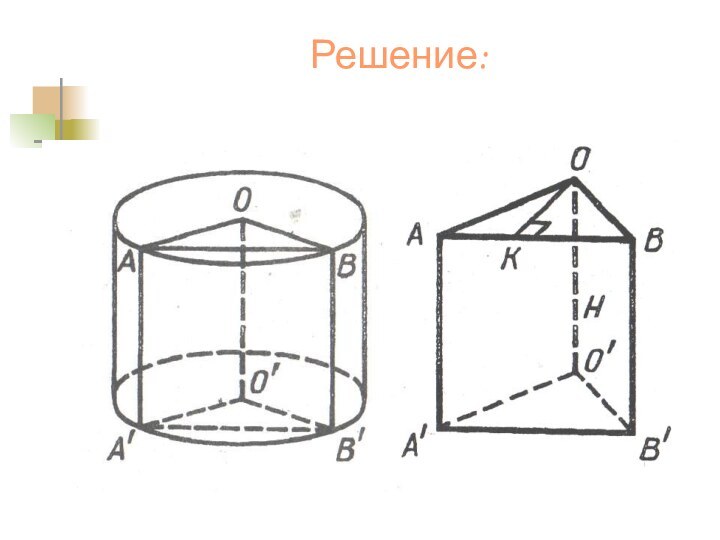


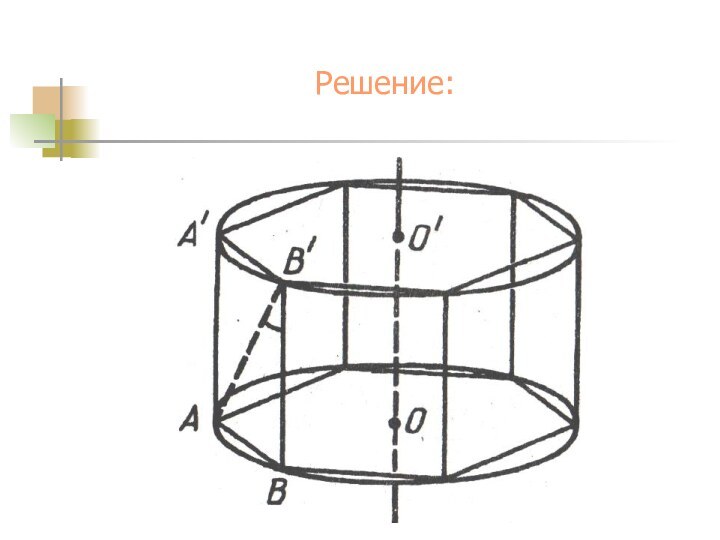











А1
В
А
В1