Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по теме Четырехугольники

Содержание

2. Параллелограмм определение свойства признаки Трапеция определение свойства признаки задачи задачи Прямоугольник определение свойство признак задачи
3. Ромб определение свойство задачи Квадрат определение свойство Итог
4. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.ABCD - параллелограммAB ǁ CDBC ǁ AD
5. Задача 1.АВСDEFDE ǁ ACEF ǁ ABОпределите вид четырехугольника ABCD
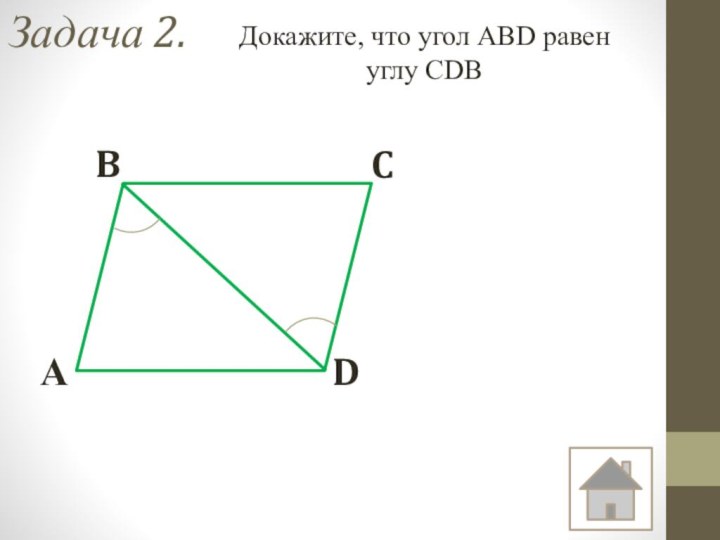
6. Задача 2.АBCDДокажите, что угол ABD равен углу CDB
7. Свойства параллелограмма 1°. В параллелограмме противоположные стороны
8. Свойства параллелограмма 2°. Диагонали параллелограмма точкой пересечения
9. Признаки параллелограмма 1°. Если в четырехугольнике две
10. 2°. Если в четырехугольнике противоположные стороны попарно
11. 3°. Если в четырехугольнике диагонали пересекаются и
12. № 1АВЕСD32oABCD – параллелограмм.Найти : С, D.
13. № 26002 см10 смNKEPMMNKP – параллелограмм.Найти: MP, PK.
14. № 3АВСD400250Найти углы параллелограмма ABCD.
15. № 4АВDEC23Найти: РABCDABCD – параллелограмм.
16. № 5ВКСАD28ABCD – параллелограмм.Найти: AD.
17. № 6ВКСАD5ABCD – параллелограмм.Найти: Р , AKD.ABCD
18. Трапецией называется четырехугольник, у которого две
19. Равнобедренная трапецияПрямоугольная трапеция
20. Свойства равнобокой трапеции 1°. В равнобокой трапеции
21. 2°. В равнобокой трапеции диагонали равны.Свойства равнобокой трапеции АBCDДано:ABCD – трапецияAB = CDДокажите:АC = BD
22. Признаки равнобокой трапеции 1°. Если в трапеции
23. № 1==50оАВСDАВСD – трапеция.Найти: В40°40°40°
24. № 2===ВСАDABCD – трапеция. Найти: углы трапеции.х2х
25. № 3АВСDK750400ABCD – трапеция, ВК // СD. Найти: углы трапеции.65°65°115°65°115°
26. № 4АВСD13545o30 смABCD – трапеция. Найти: ВС.o45°45°90°45°
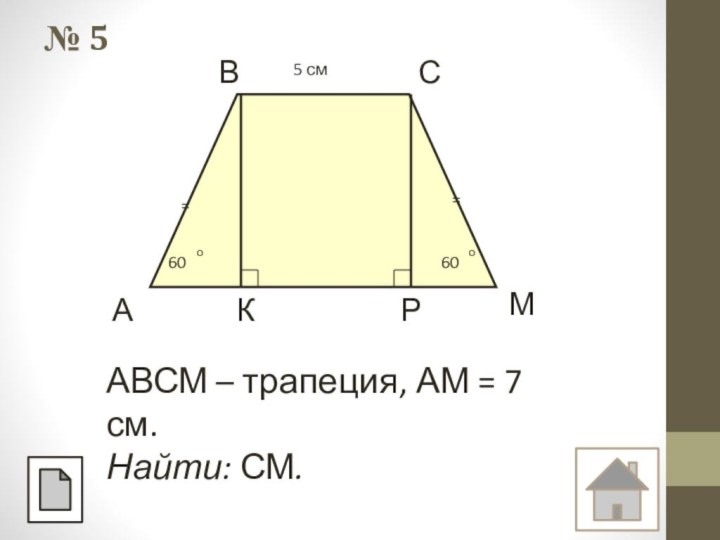
27. № 5==6060оо5 смАВСКРМАВСМ – трапеция, АМ = 7 см.Найти: СМ.
28. Прямоугольником называется параллелограмм, у которого все углы прямые.ABCD - прямоугольник
29. Свойство прямоугольника Диагонали прямоугольника равны.Дано:ABCD – прямоугольникДокажите:АC = BD
30. Признак прямоугольникаЕсли в параллелограмме диагонали равны, то
31. № 1АВСDOKABCD – прямоугольник.Найти: АВК .?40°50°
32. № 230о====____ABCDEFKMАСЕК – прямоугольник, ВС = 5 см.Найти: Р .BDFM5 см5 см10 см
33. № 3АВСО60°DABCD – прямоугольник.Найти: АОВ, ВОС??60°60°60°120°
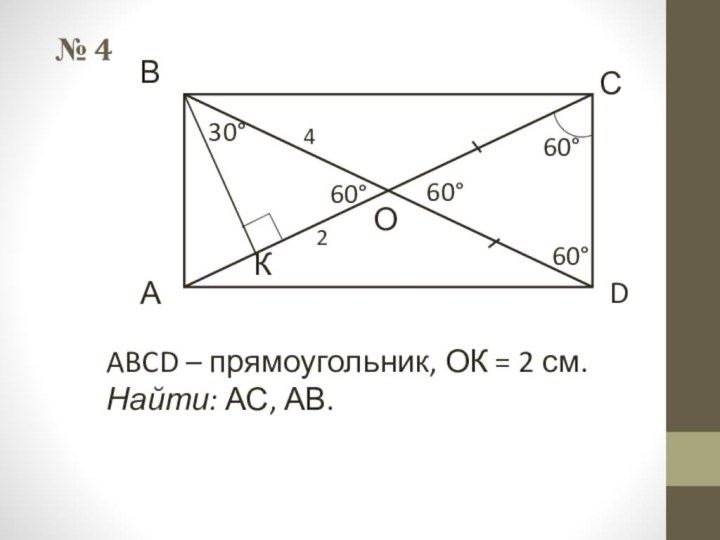
34. № 4АВСDABCD – прямоугольник, ОК = 2 см.Найти: АС, АВ.260°60°60°60°30°4
35. № 5АВСКD4 смABCD – прямоугольник.Найти: AD.45°45°4 см60°30°3 см
36. Ромбом называется параллелограмм, у которого все стороны равны.ABCD - ромб
37. Свойство ромба Диагонали ромба взаимно перпендикулярны и
38. № 155оАВСDABCD – ромб.Найти: BAD.55°70°70°
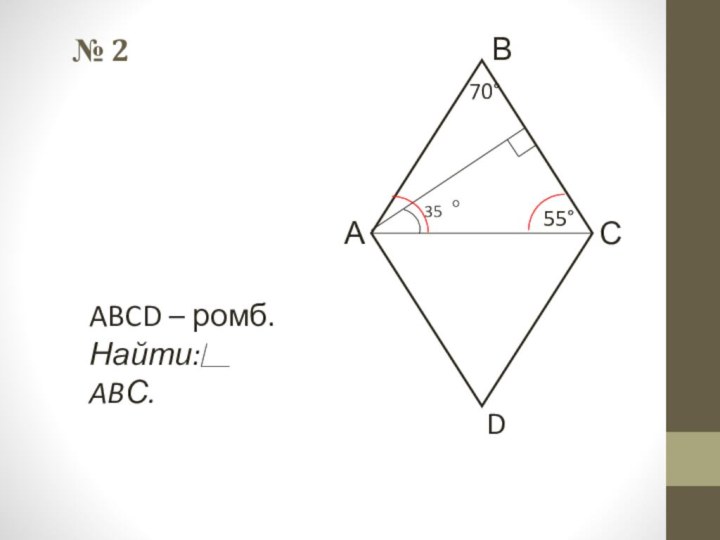
39. № 235оАВСDABCD – ромб.Найти: ABС.55°70°
40. № 3АВСЕКDABCD – ромб.Найти: СВЕ.75о75°15°
41. № 46 см60оАВСDMNABCD – ромб.Найти: MD + DN.30°3 см3 см60°30°3 см3 см
42. Квадратом называется прямоугольник, у которого все стороны равны.ABCD - квадрат
43. Свойства квадрата 1°. Все углы квадрата прямые
45. 1) Диагональ квадрата 24 см. Найдите периметр
46. 4) Найдите углы параллелограмма, если одна из
47. Скачать презентацию
48. Похожие презентации

Параллелограмм определение свойства признаки Трапеция определение свойства признаки задачи задачи Прямоугольник определение свойство признак задачи

Главная
Геометрия
Презентация по теме Четырехугольники

Параллелограмм определение свойства признаки Трапеция определение свойства признаки задачи задачи Прямоугольник определение свойство признак задачи

Ромб определение свойство задачи Квадрат определение свойство Итог

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.ABCD - параллелограммAB ǁ CDBC ǁ AD

Задача 1.АВСDEFDE ǁ ACEF ǁ ABОпределите вид четырехугольника ABCD

Задача 2.АBCDДокажите, что угол ABD равен углу CDB

Свойства параллелограмма 1°. В параллелограмме противоположные стороны равны и противоположные углы равны

Свойства параллелограмма 2°. Диагонали параллелограмма точкой пересечения делятся пополам .АBCDО1234Дано:ABCD – параллелограммДокажите:AО

Признаки параллелограмма 1°. Если в четырехугольнике две стороны равны и параллельны, то

2°. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник -

3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то

№ 1АВЕСD32oABCD – параллелограмм.Найти : С, D.

№ 26002 см10 смNKEPMMNKP – параллелограмм.Найти: MP, PK.

№ 3АВСD400250Найти углы параллелограмма ABCD.

№ 4АВDEC23Найти: РABCDABCD – параллелограмм.

№ 5ВКСАD28ABCD – параллелограмм.Найти: AD.

№ 6ВКСАD5ABCD – параллелограмм.Найти: Р , AKD.ABCD

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие

Равнобедренная трапецияПрямоугольная трапеция

Свойства равнобокой трапеции 1°. В равнобокой трапеции углы при основании равны.АBCDДано:ABCD –

2°. В равнобокой трапеции диагонали равны.Свойства равнобокой трапеции АBCDДано:ABCD – трапецияAB = CDДокажите:АC = BD

Признаки равнобокой трапеции 1°. Если в трапеции углы при основании равны, то

№ 1==50оАВСDАВСD – трапеция.Найти: В40°40°40°

№ 2===ВСАDABCD – трапеция. Найти: углы трапеции.х2х

№ 3АВСDK750400ABCD – трапеция, ВК // СD. Найти: углы трапеции.65°65°115°65°115°

№ 4АВСD13545o30 смABCD – трапеция. Найти: ВС.o45°45°90°45°

№ 5==6060оо5 смАВСКРМАВСМ – трапеция, АМ = 7 см.Найти: СМ.

Прямоугольником называется параллелограмм, у которого все углы прямые.ABCD - прямоугольник

Свойство прямоугольника Диагонали прямоугольника равны.Дано:ABCD – прямоугольникДокажите:АC = BD

Признак прямоугольникаЕсли в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.Дано:ABCD –

№ 1АВСDOKABCD – прямоугольник.Найти: АВК .?40°50°

№ 230о====____ABCDEFKMАСЕК – прямоугольник, ВС = 5 см.Найти: Р .BDFM5 см5 см10 см

№ 3АВСО60°DABCD – прямоугольник.Найти: АОВ, ВОС??60°60°60°120°

№ 4АВСDABCD – прямоугольник, ОК = 2 см.Найти: АС, АВ.260°60°60°60°30°4

№ 5АВСКD4 смABCD – прямоугольник.Найти: AD.45°45°4 см60°30°3 см

Ромбом называется параллелограмм, у которого все стороны равны.ABCD - ромб

Свойство ромба Диагонали ромба взаимно перпендикулярны и делят углы пополам.Дано:ABCD – ромбДокажите:АC

№ 155оАВСDABCD – ромб.Найти: BAD.55°70°70°

№ 3АВСЕКDABCD – ромб.Найти: СВЕ.75о75°15°

№ 46 см60оАВСDMNABCD – ромб.Найти: MD + DN.30°3 см3 см60°30°3 см3 см

Квадратом называется прямоугольник, у которого все стороны равны.ABCD - квадрат

Свойства квадрата 1°. Все углы квадрата прямые .2°. Диагонали квадрата равны, взаимно

1) Диагональ квадрата 24 см. Найдите периметр четырехугольника, образованного отрезками, последовательно соединяющими

4) Найдите углы параллелограмма, если одна из его диагоналей является высотой и

Домашнее задание:1) Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см

Слайды презентации

Слайд 2 Параллелограмм
определение
свойства
признаки
Трапеция
определение
свойства
признаки

задачи
задачи
Прямоугольник
определение
свойство
признак
задачи

Слайд 3 Ромб
определение
свойство
задачи
Квадрат
определение
свойство
Итог

Слайд 4 Параллелограммом называется четырехугольник, у которого противоположные стороны

попарно параллельны.
ABCD - параллелограмм
AB ǁ CD
BC ǁ AD

Слайд 5 Задача 1.
А
В
С
D
E
F
DE ǁ AC
EF ǁ AB
Определите вид четырехугольника

ABCD

Слайд 6 Задача 2.
А
B
C
D
Докажите, что угол ABD равен углу CDB

Слайд 7 Свойства параллелограмма
1°. В параллелограмме противоположные стороны равны

Свойства параллелограмма 1°. В параллелограмме противоположные стороны равны и противоположные углы

и противоположные углы равны .
А
B
C
D
Дано:
ABCD – параллелограмм
Докажите:
AB = CD;

BC = AD;
A = B; C = D

Слайд 8 Свойства параллелограмма
2°. Диагонали параллелограмма точкой пересечения делятся

Свойства параллелограмма 2°. Диагонали параллелограмма точкой пересечения делятся пополам .АBCDО1234Дано:ABCD –

пополам .
А
B
C
D
О
1
2
3
4
Дано:
ABCD – параллелограмм
Докажите:
AО = ОС; BO = DO

Слайд 9 Признаки параллелограмма
1°. Если в четырехугольнике две стороны

Признаки параллелограмма 1°. Если в четырехугольнике две стороны равны и параллельны,

равны и параллельны, то этот четырехугольник - параллелограмм .
А
B
C
D
Дано:
AB

= CD; АВ ǁ CD
Докажите:
ABCD – параллелограмм

Слайд 10 2°. Если в четырехугольнике противоположные стороны попарно равны,

то этот четырехугольник - параллелограмм .
Признаки параллелограмма
Дано:
AB =

CD; BC = AD
Докажите:
ABCD – параллелограмм

Слайд 11 3°. Если в четырехугольнике диагонали пересекаются и точкой

3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам,

пересечения делятся пополам, то этот четырехугольник - параллелограмм.
Признаки параллелограмма

Дано:
AO = OC; BO = OD
Докажите:
ABCD – параллелограмм

Слайд 12 № 1
А
В
Е
С
D
32
o
ABCD – параллелограмм.
Найти : С,

D.

Слайд 13 № 2
60
0
2 см
10 см
N
K
E
P
M
MNKP – параллелограмм.
Найти: MP, PK.

Слайд 14 № 3
А
В
С
D
40
0
25
0
Найти углы параллелограмма ABCD.

Слайд 15 № 4
А
В
D
E
C
2
3
Найти: Р
ABCD
ABCD – параллелограмм.

Слайд 16 № 5
В
К
С
А
D
2
8
ABCD – параллелограмм.
Найти: AD.

Слайд 17 № 6
В
К
С
А
D
5
ABCD – параллелограмм.
Найти: Р

, AKD.
ABCD

Слайд 18 Трапецией называется четырехугольник, у которого две стороны

параллельны, а две другие стороны не параллельны.
А
B
C
D
ABCD - трапеция
BC,

AD - основания

AB, CD – боковые стороны

Слайд 19 Равнобедренная трапеция
Прямоугольная трапеция

Слайд 20 Свойства равнобокой трапеции
1°. В равнобокой трапеции углы

при основании равны.
А
B
C
D
Дано:
ABCD – трапеция
AB = CD
Докажите:
А

= D

Слайд 21 2°. В равнобокой трапеции диагонали равны.
Свойства равнобокой трапеции

А
B
C
D
Дано:
ABCD – трапеция
AB = CD
Докажите:
АC = BD

Слайд 22 Признаки равнобокой трапеции
1°. Если в трапеции углы

Признаки равнобокой трапеции 1°. Если в трапеции углы при основании равны,

при основании равны, то трапеция равнобокая.
2°. Если в трапеции

диагонали равны, то трапеция равнобокая.

Слайд 23 № 1
=
=
50
о
А
В
С
D
АВСD – трапеция.
Найти: В
40°
40°
40°

Слайд 24 № 2
=
=
=
В
С
А
D
ABCD – трапеция.
Найти: углы трапеции.
х
2х

Слайд 25 № 3
А
В
С
D
K
75
0
40
0
ABCD – трапеция, ВК // СD.
Найти:

углы трапеции.

65°
65°
115°
65°
115°

Слайд 26 № 4
А
В
С
D
135
45
o
30 см
ABCD – трапеция.
Найти: ВС.
o
45°
45°
90°
45°

Слайд 27 № 5
=
=
60
60
о
о
5 см
А
В
С
К
Р
М
АВСМ – трапеция, АМ = 7

см.
Найти: СМ.

Слайд 28 Прямоугольником называется параллелограмм, у которого все углы

прямые.
ABCD - прямоугольник

Слайд 29 Свойство прямоугольника
Диагонали прямоугольника равны.
Дано:
ABCD – прямоугольник
Докажите:
АC =

BD

Слайд 30 Признак прямоугольника
Если в параллелограмме диагонали равны, то этот

параллелограмм - прямоугольник.
Дано:
ABCD – параллелограмм
АC = BD
Докажите:
ABCD –

прямоугольник

Слайд 31 № 1
А
В
С
D
O
K
ABCD – прямоугольник.
Найти: АВК .
?
40°
50°

Слайд 32 № 2
30
о
=
=
=
=
_
_
_
_
A
B
C
D
E
F
K
M
АСЕК – прямоугольник, ВС = 5 см.
Найти:

Р .
BDFM
5 см
5 см
10 см

Слайд 33 № 3
А
В
С
О
60°
D
ABCD – прямоугольник.
Найти:

АОВ, ВОС
?
?
60°
60°
60°
120°

Слайд 34 № 4
А
В
С
D
ABCD – прямоугольник, ОК = 2 см.
Найти:

АС, АВ.
2
60°
60°
60°
60°
30°
4

Слайд 35 № 5
А
В
С
К
D
4 см
ABCD – прямоугольник.
Найти: AD.
45°
45°
4 см
60°
30°
3 см

Слайд 36 Ромбом называется параллелограмм, у которого все стороны

равны.
ABCD - ромб

Слайд 37 Свойство ромба
Диагонали ромба взаимно перпендикулярны и делят

Свойство ромба Диагонали ромба взаимно перпендикулярны и делят углы пополам.Дано:ABCD –

углы пополам.
Дано:
ABCD – ромб
Докажите:
АC BD
ВАС

= DAC

Слайд 38 № 1
55
о
А
В
С
D
ABCD – ромб.
Найти: BAD.
55°
70°
70°

Слайд 39 № 2
35
о
А
В
С
D
ABCD – ромб.
Найти: ABС.
55°
70°

Слайд 40 № 3
А
В
С
Е
К
D
ABCD – ромб.
Найти: СВЕ.
75
о
75°
15°

Слайд 41 № 4
6 см
60
о
А
В
С
D
M
N
ABCD – ромб.
Найти: MD + DN.
30°
3

см
3 см
60°
30°
3 см
3 см

Слайд 42 Квадратом называется прямоугольник, у которого все стороны

равны.
ABCD - квадрат

Слайд 43 Свойства квадрата
1°. Все углы квадрата прямые .
2°.

Свойства квадрата 1°. Все углы квадрата прямые .2°. Диагонали квадрата равны,

Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам

Слайд 44

Слайд 45 1) Диагональ квадрата 24 см. Найдите периметр четырехугольника,

1) Диагональ квадрата 24 см. Найдите периметр четырехугольника, образованного отрезками, последовательно

образованного отрезками, последовательно соединяющими середины сторон данного квадрата.
2) В

ромбе ABCD угол А = 31°. Диагонали пересекаются в точке О. Найдите углы треугольника ВОС.
3) Найдите меньшее основание равнобедренной трапеции, если её большее основание равно 16 см, боковая сторона 10 см, а один из углов равен 60°.

Слайд 46 4) Найдите углы параллелограмма, если одна из его

4) Найдите углы параллелограмма, если одна из его диагоналей является высотой

диагоналей является высотой и равна одной из сторон.
5) Найдите

углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.
6) В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ, углы ADB и BDC равны 30°. Найдите длину AD, если периметр трапеции равен 60 см.