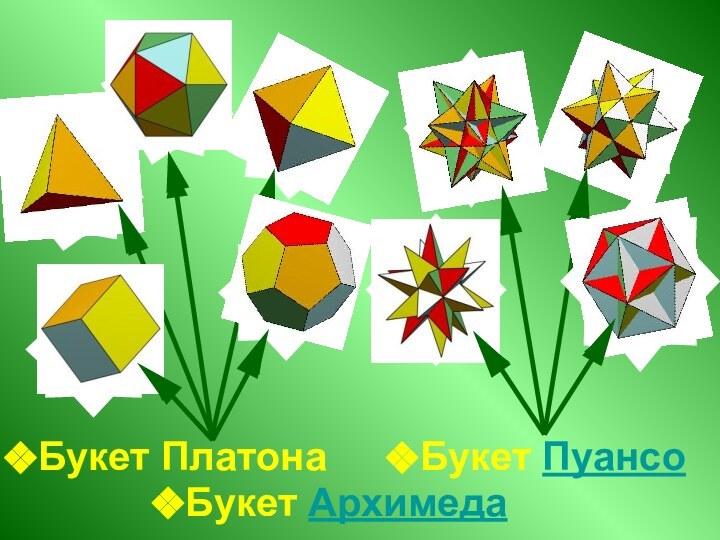
виды.
Формула Эйлера для выпуклых многогранников.
Формулы для вычисления объема и
площади поверхности правильных многогранников.Использование формы правильных многогранников природой и человеком.
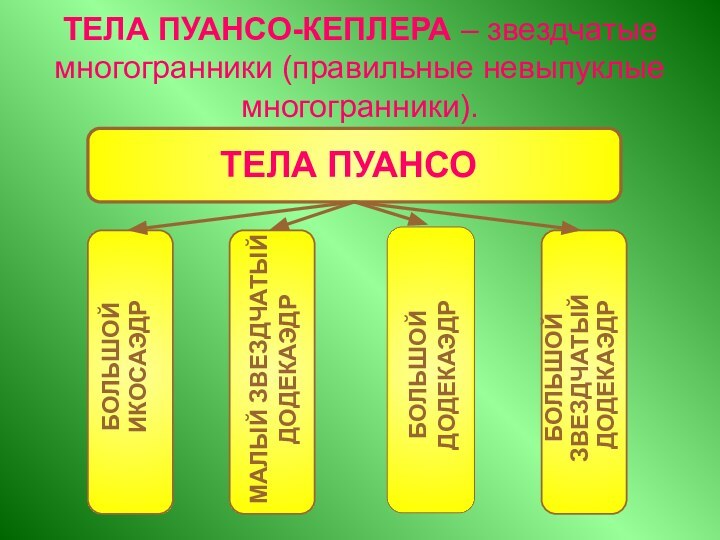
Звездчатые многогранники, их виды.
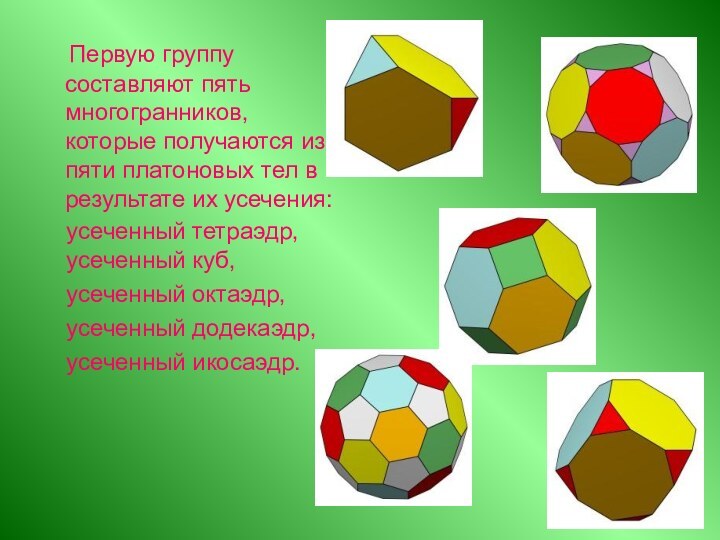
Архимедовы тела, их виды.