- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Касательная к графику функции
Содержание
- 2. Содержание:Появление понятия касательнойИстория появления касательнойПостроение касательнойПример построения касательной: 1 часть 2 часть 3 часть
- 3. Появление понятия касательной Понятие касательной – одно из
- 4. История появления касательной Интерес к касательным возродился в
- 5. Построение касательной Построение касательных – одна из тех
- 6. Пример построения касательной Пусть кривая есть график функции
- 7. Если существует предел то прямую и называют
- 8. Скачать презентацию
- 9. Похожие презентации
Содержание:Появление понятия касательнойИстория появления касательнойПостроение касательнойПример построения касательной: 1 часть 2 часть 3 часть





Слайд 2
Содержание:
Появление понятия касательной
История появления касательной
Построение касательной
Пример построения касательной:
Слайд 3
Появление понятия касательной
Понятие касательной – одно из древнейших
в математике. В геометрии касательную к окружности определяют как
прямую, имеющую ровно одну точку пересечения с этой окружностью. Древние с помощью циркуля и линейки умели проводить касательные к окружности, а в последствии – к коническим сечениям: эллипсам, гиперболам и параболам.√ вернуться к содержанию
Слайд 4
История появления касательной
Интерес к касательным возродился в Новое
время. Тогда были открыты кривые, которых не знали учёные
древности. Например, Галилей ввёл циклоиду, а Декарт и Ферма построили к ней касательную. В первой трети XVII в. Начали понимать, что касательная – прямая, «наиболее тесно примыкающая» к кривой в малой окрестности заданной точки. Легко представить себе такую ситуацию, когда нельзя построить касательную к кривой в данной точке (рисунок).√ вернуться к содержанию
Слайд 5
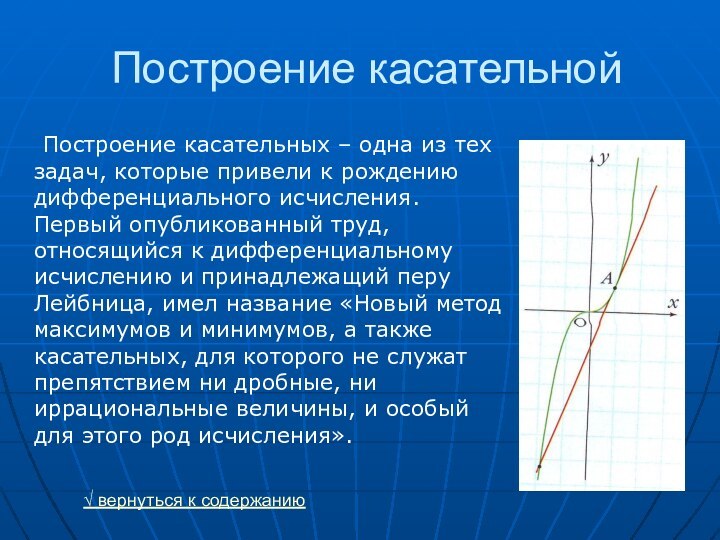
Построение касательной
Построение касательных – одна из тех задач,
которые привели к рождению дифференциального исчисления. Первый опубликованный труд,
относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название «Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления».√ вернуться к содержанию
Слайд 6
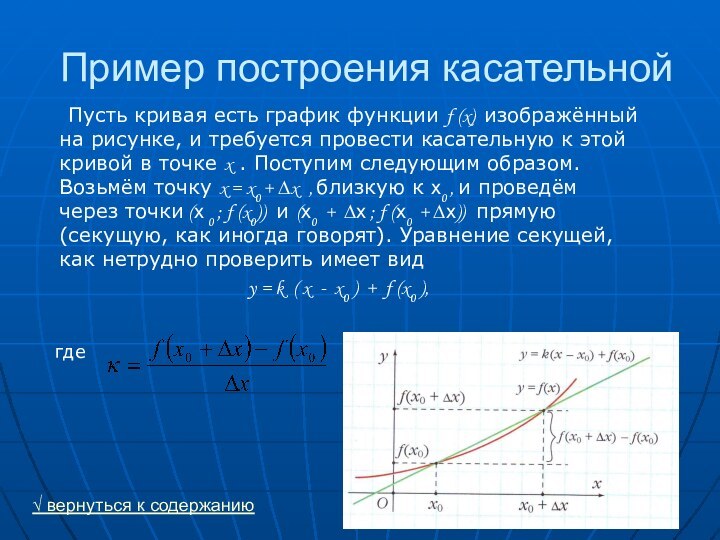
Пример построения касательной
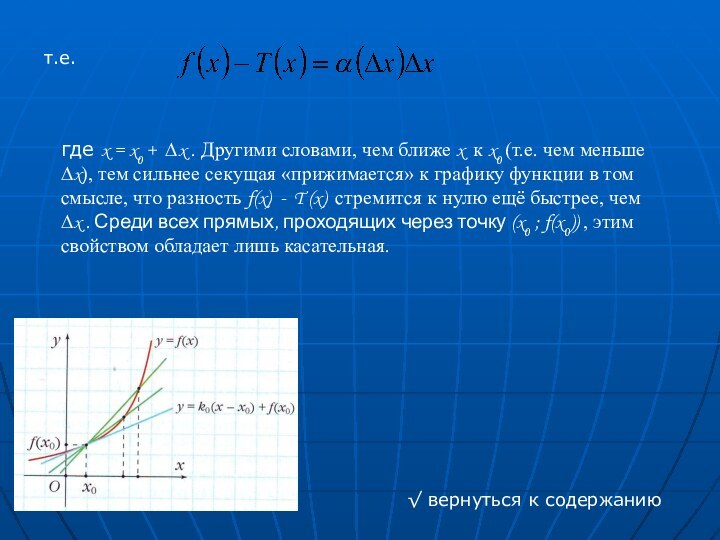
Пусть кривая есть график функции f
(x) изображённый на рисунке, и требуется провести касательную к
этой кривой в точке x . Поступим следующим образом. Возьмём точку x = x0 + ∆x , близкую к х0 , и проведём через точки (х 0 ; f (x0)) и (х0 + ∆х ; f (х0 + ∆х)) прямую (секущую, как иногда говорят). Уравнение секущей, как нетрудно проверить имеет видy = k ( x - x0 ) + f (x0 ),
где
√ вернуться к содержанию
Слайд 7
Если существует предел
то прямую
и называют касательной
к графику функции f(x) в точке x0 .
Если сказать иначе, касательную можно определить как прямую, которая является предельным положением секущих, когда ∆x стремится к 0.Из определения величины k0 видно, что функция
√ вернуться к содержанию
Стремится к 0, когда ∆x стремится к 0. Последнее равенство означает, что