Слайд 2
Определение
Две прямые в пространстве называются параллельными, если они
не пересекаются и лежат в одной плоскости.
Значит, через две
параллельные прямые можно провести плоскость и только одну.
a
b
a ΙΙ b
Слайд 3
Теорема
Через любую точку
пространства, не лежащую на данной прямой, можно
провести прямую, параллельную данной, и только одну.
Дано: a,
M не принадлежит a
Доказать:
1. через прямую a можно
провести прямую b ΙΙ a.
2. прямая b -единственная
Слайд 4
Лемма
Дано: a ΙΙ b, a ∩ α
Доказать: b∩α
Слайд 5
Если одна из параллельных
прямых пересекает плоскость, то и вторая прямая пересекает эту
плоскость.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Если две прямые параллельны третьей прямой, то они параллельны между собой.
Слайд 6
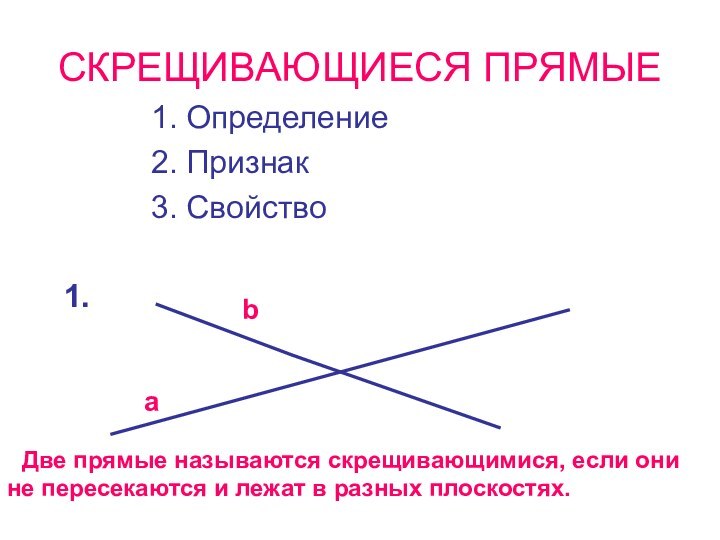
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
1. Определение
2. Признак
3. Свойство
1.
a
b
Две
прямые называются скрещивающимися, если они не пересекаются и лежат
в разных плоскостях.
Слайд 7
Признак скрещивающихся прямых
Если b є α, a ∩
α = M, M є b,
то прямые a
и b скрещиваются.
Слайд 8
Если одна прямая лежит в плоскости, а другая
прямая пересекает эту плоскость в точке, не лежащей на
первой прямой, то прямые скрещиваются.
C
Найти скрещивающиеся прямые
Слайд 9
Свойство скрещивающихся прямых
Через каждую из скрещивающихся прямых можно
провести плоскость, параллельную другой прямой.
Слайд 11
Задача № 21
Доказать:
прямые a и b пересекают
плоскости (ABC) и (ABD)
Задача № 40
Дано: прямые а
и b скрещиваются,
М є а, N є b,
плоскость α проведена через
а и точку N,
плоскость β проведена
через b и точку M.
Лежит ли прямая b в плоскости α?
Пересекаются ли плоскости α и β?
Слайд 13
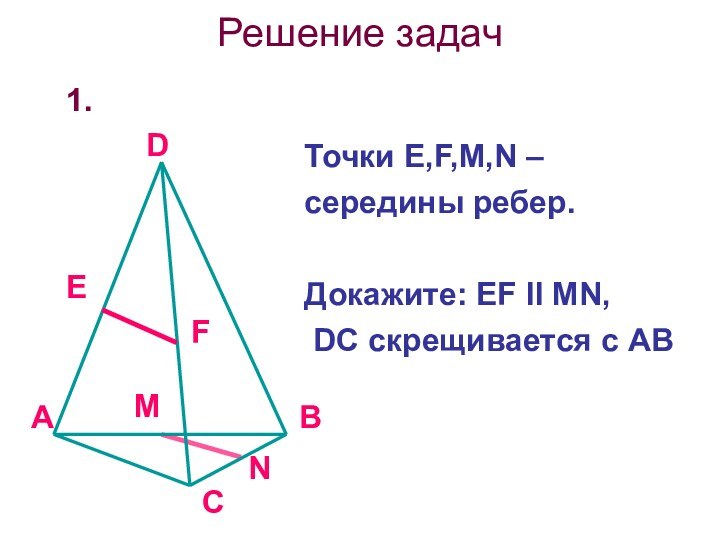
Решение задач
1.
Точки Е,F,M,N – середины ребер.
Докажите: EF ll
MN,
DC скрещивается с AB
Слайд 15
2.
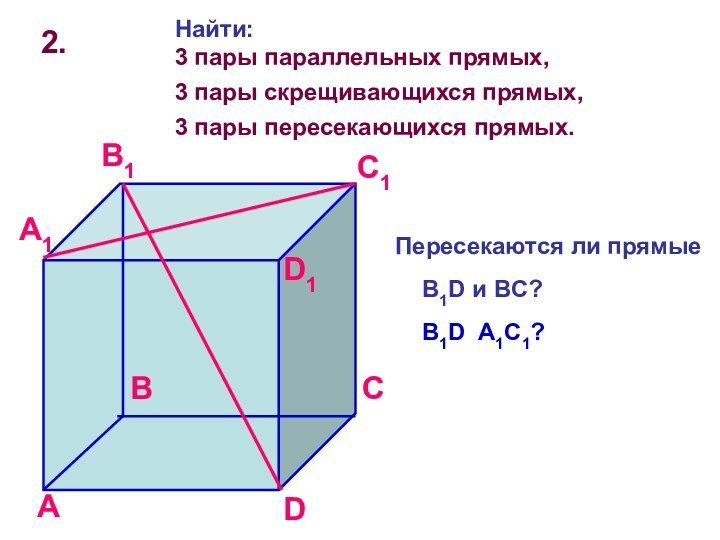
Найти:
3 пары параллельных прямых,
3 пары скрещивающихся прямых,
3
пары пересекающихся прямых.
Пересекаются ли прямые
B1D и BC?
B1D
A1C1?
Слайд 16
Самостоятельная работа
1 вариант
2 вариант
KMNF - трапеция KBDF - параллелограмм
Доказать:
AB ll CD BD ll CA
ME скрещивается с CD DE скрещивается с CA
Пересекаются ли прямые
ME и AB? BA и CЕ?
Слайд 17
Взаимное расположение прямой и плоскости в пространстве
1. Прямая
и плоскость имеют одну общую точку.
Слайд 18
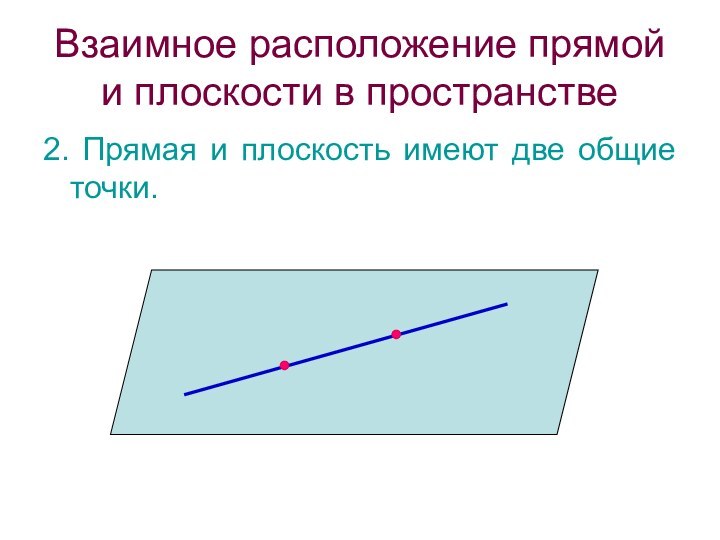
Взаимное расположение прямой и плоскости в пространстве
2. Прямая
и плоскость имеют две общие точки.
Слайд 19
Расположение прямой и плоскости
3. Прямая и плоскость не
имеют общих точек.
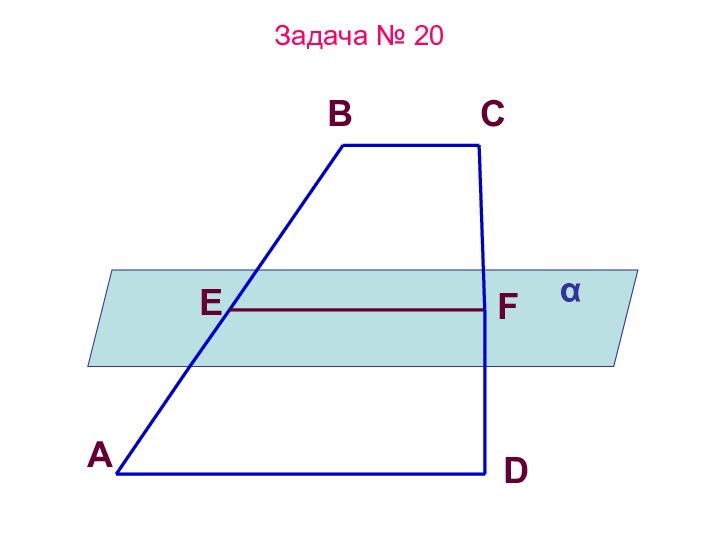
Слайд 20
Расположение прямой и плоскости
1. Если прямая и плоскость
имеют одну общую точку, то прямая пересекает эту плоскость.
2.
Если прямая и плоскость имеют две общие точки, то все точки этой прямой лежат в плоскости, то есть прямая лежит в плоскости.
3. Если прямая и плоскость не имеют общих точек, то прямая параллельна плоскости.
Какая же прямая называется параллельной плоскости?
Слайд 21
Признак параллельности прямой и плоскости
Если прямая, не лежащая
в плоскости, параллельна какой-нибудь прямой плоскости, то она параллельна
этой плоскости.
Дано: прямая allb,
a є α, b є α.
Доказать:allα
Слайд 22
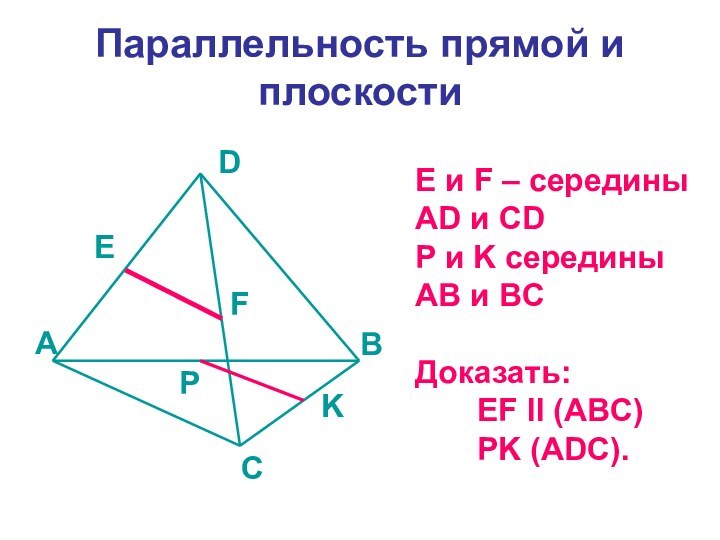
Параллельность прямой и плоскости
E и F – середины
AD и CD
P и K середины AB и BC
Доказать:
EF ll (ABC)
PK (ADC).
A
B
C
D
E
F
K
P
Слайд 23
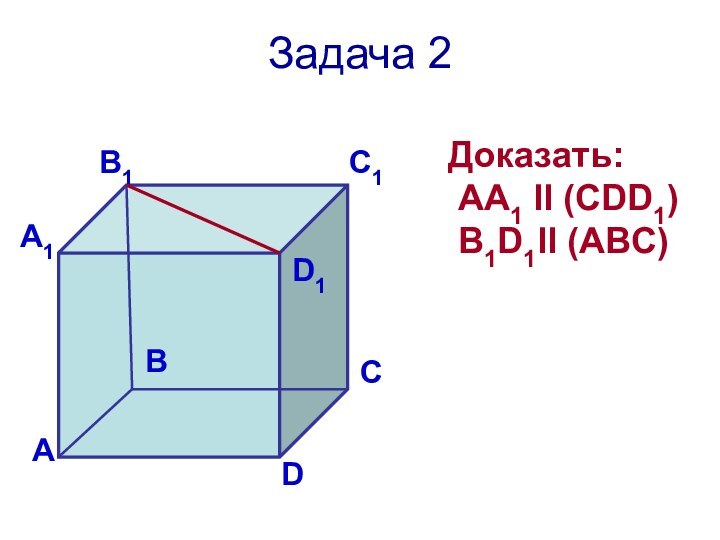
Задача 2
Доказать:
АА1 ll (CDD1)
B1D1ll (ABC)
Слайд 24
Свойства
Дано: aєα, allβ, α ∩ β = c
Доказать:
allc
Слайд 25
Свойство 1
Если прямая, лежащая в одной из пересекающихся
плоскостей, параллельна другой плоскости, то она параллельна их линии
пересечения.
Слайд 26
Свойство 2
Если одна из параллельных прямых параллельна данной
плоскости, то вторая прямая либо лежит в этой плоскости,
либо также параллельна данной плоскости.
Слайд 27
УГОЛ МЕЖДУ ПРЯМЫМИ
1. Угол между пересекающимися прямыми.
2. Угол
между скрещивающимися прямыми.
Слайд 28
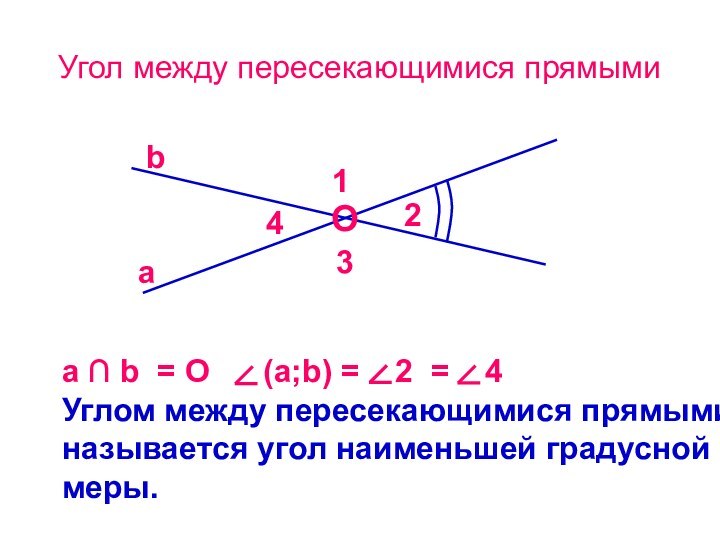
Угол между пересекающимися прямыми
Слайд 29
Угол между скрещивающимися прямыми
Углом между скрещивающимися прямыми называется
угол между пересекающимися прямыми, параллельными данным скрещивающимся.
a
(a ,b)
= ( a1,b1)
Слайд 30
Решение задач
1.
А
В
С
D
M
ABCD – прямоугольник.
Найти угол между прямыми:
MB
и AD,
AM и CD,
AM и BC.
Слайд 31
2.
Найти угол между прямыми
AB и CD.
Слайд 32
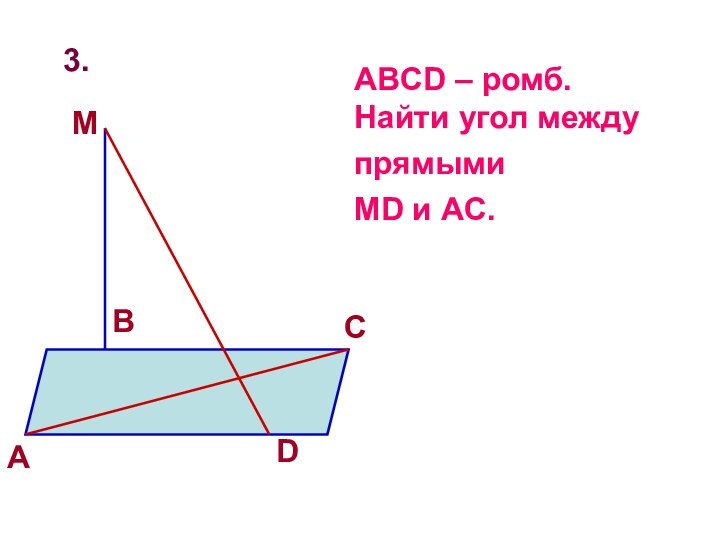
3.
M
ABCD – ромб.
Найти угол между прямыми
MD и
Слайд 33
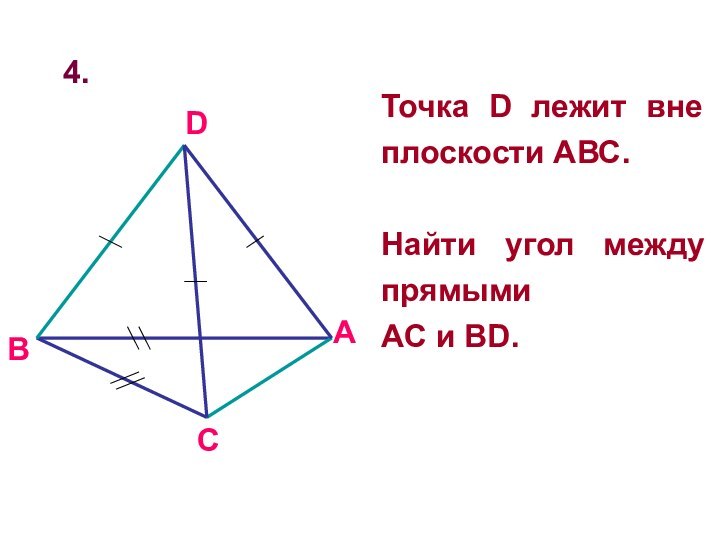
4.
Точка D лежит вне плоскости АВС.
Найти угол между
прямыми
AC и BD.
Слайд 34
5.
D
ABCD – квадрат.
Найти угол между прямыми CM и
Слайд 35
Параллельность плоскостей
1. Определение.
2. Признак.
3. Свойства.
ОПРЕДЕЛЕНИЕ
Плоскости называются параллельными,
если они не имеют общих точек.
ПРИЗНАК
Если две пересекающиеся прямые
одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны.
Слайд 36
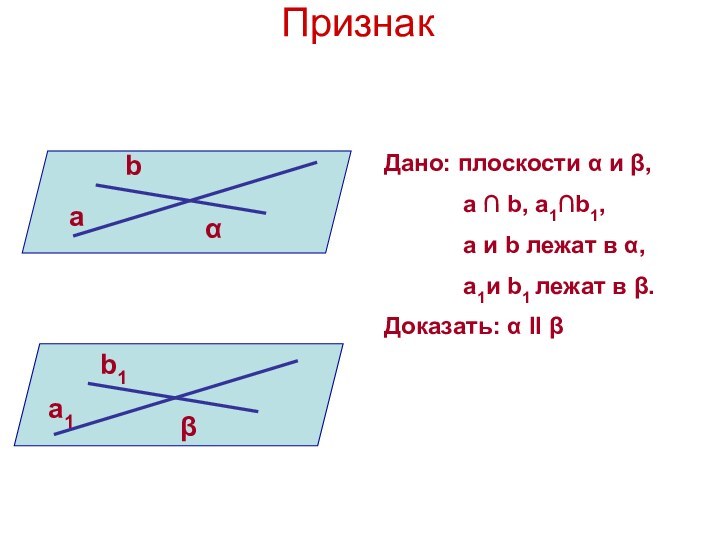
Признак
Дано: плоскости α и β,
a ∩ b, a1∩b1,
a и b лежат в α,
a1и b1 лежат в β.
Доказать: α II β
Слайд 37
Свойства
1. Если две параллельные плоскости пересечены третьей, то
линии пересечения плоскостей параллельны.
Дано: α II β, γ ∩
α = a,
γ ∩ β = b.
Доказать: α II β
Слайд 38
Свойства
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями,
равны.
Дано: α II β, a II b.
Доказать: AD
= BC
α
β
a
b
А
B
C
D
Слайд 39
Свойства
3. Если прямая пересекает одну из параллельных плоскостей,
то она пересекает и другую.
4. Если плоскость пересекает одну
из параллельных плоскостей, то она пересекает и вторую плоскость.
5. В пространстве через точку, не лежащую на данной плоскости, можно провести плоскость, параллельную данной, притом только одну.
Слайд 40
Решение задач
Доказать параллельность плоскостей ABC и A1B1C1
AA1
II BB1 II CC1
AA1 = BB1 = CC1
AA1C1C и CС1B1B - параллелограммы
Слайд 41
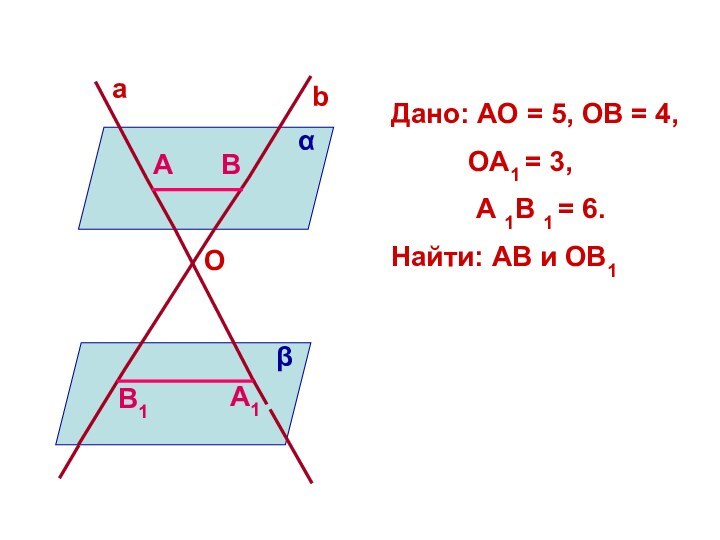
Дано: АО = 5, ОВ = 4,
ОА1 = 3,
А 1В 1 = 6.
Найти: АВ и ОВ1
Слайд 42
Задача № 64
a
Доказать:
треугольники
А1 В1 С1
и А2 В2 С2
подобны