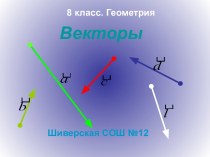
(а также длина такого отрезка),
называется высотой конуса. Если
основание конуса
имеет центр симметрии (например, является кругом
или эллипсом) и ортогональная проекция вершины
конуса на плоскость основания совпадает с этим центром,
то конус называется прямым. При этом прямая,
соединяющая вершину и центр основания, называется
осью конуса. Если же ортогональная проекция
вершины не совпадает с центром симметрии основания,
то конус называется косым или наклонным. Если
основание конуса является кругом, конус называется
круговым. Прямой круговой конус (часто
его называют просто конусом) можно получить
Вращением.Прямоугольного треугольника
вокруг прямой, содержащей катет (эта прямая
представляет собой ось конуса).
A
B
C
O
F
E
D
W
S
P
N
M
L
K
G





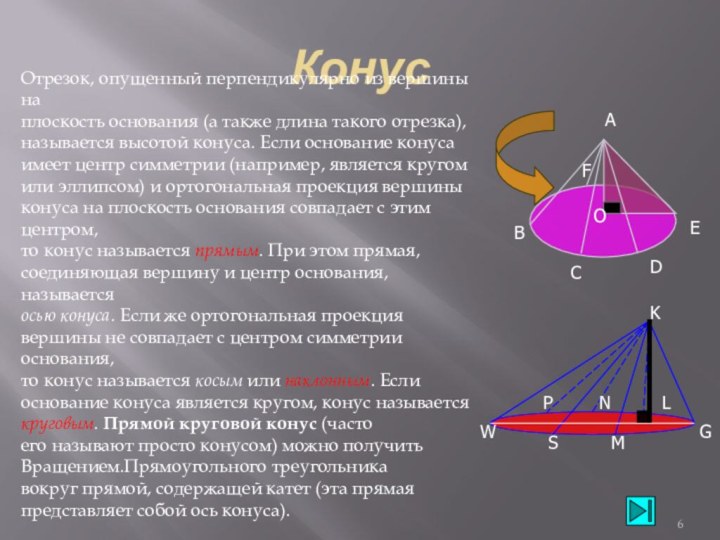

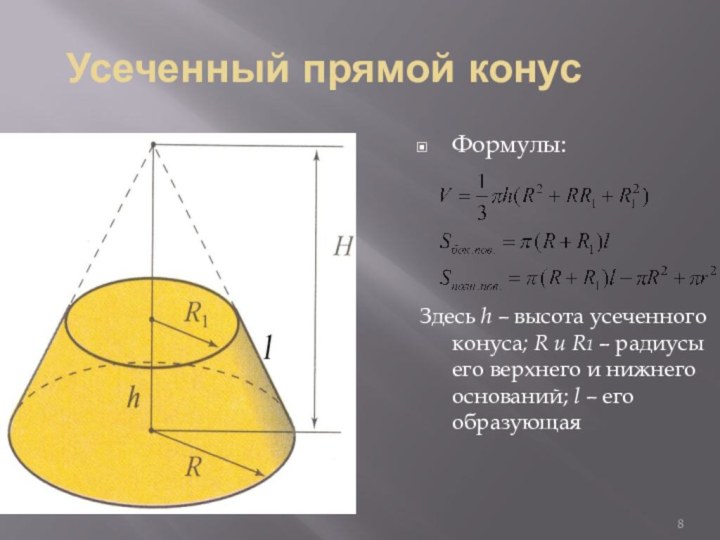
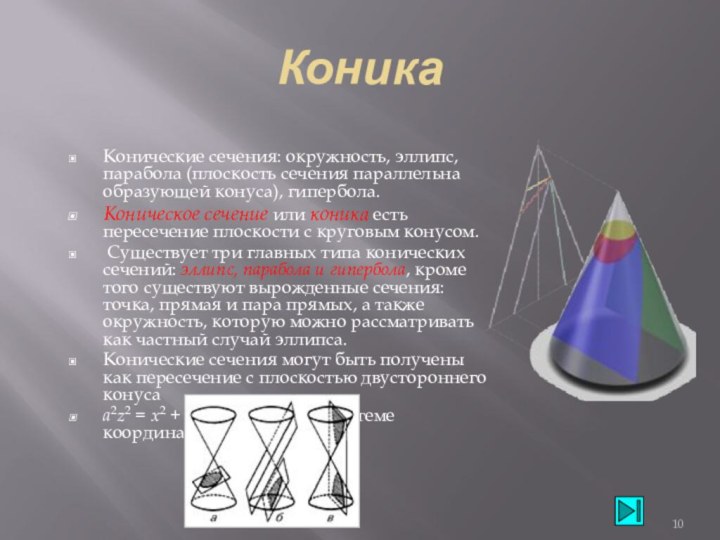





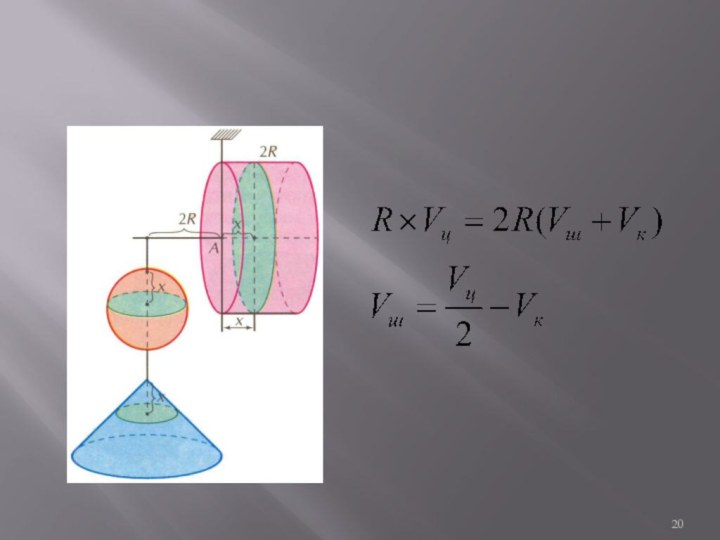
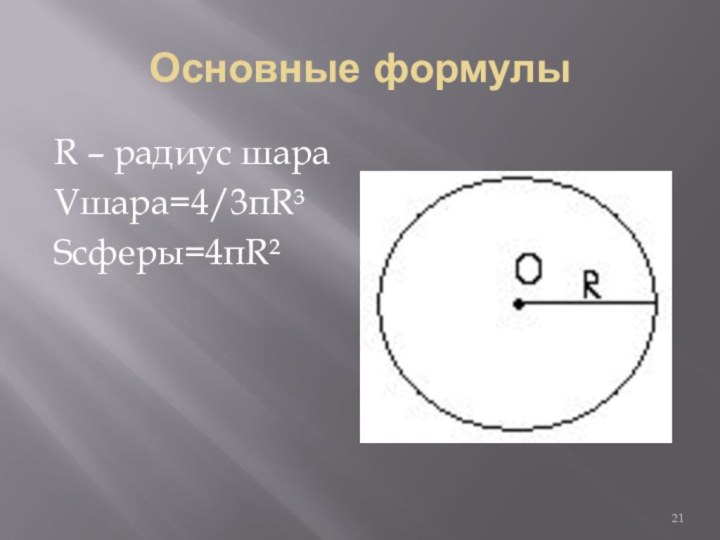
![Методическая разработка по теме Тела вращения.Конус,сфера Как Архимед находил объем шараПлощади сечений: Sц, Sш, Sк.Sц=4πR²;Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;Sк=π[CD]²= πx²](/img/tmb/6/575129/131705b91bc04b063b5e43034f61bdaf-720x.jpg)