Презентация на тему Решение задач на смеси, растворы и сплавы

металлы находятся в отношении 2: 3, а в другом

в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?

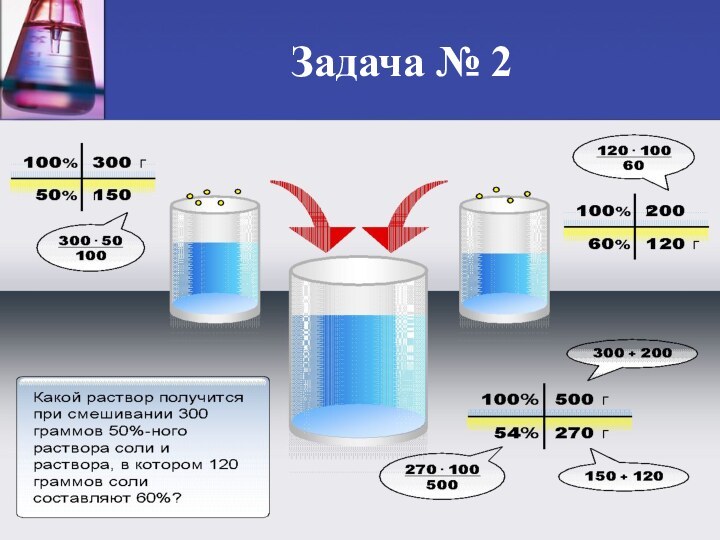
По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
*х + * у = * 1
Аналогично массу серебра и получаем уравнение
* х + * у = * 1
Записываем одну из систем:
х + у = 1
х + у =
х + у = 1
х + у =
Решая ее, получаем х = 0,125 и у = 0,875
Ответ: 125 г и 875 г.

содержит 15% меди, а другой 65%. Сколько нужно взять

каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

1. Изобразим сплавы в виде прямоугольников
М С М С
+ =
х(г) (200 –х) (г) 200 (г)
0,15х + 0,65(200 – х) = 0,3 *200 х = 140
2. Обозначим
М С М С
+ =
х(г) у(г) 200(г)
х + у = 200
0,15х + 0,65у =0,3 *200
х = 140 и у = 60
Ответ: 140г меди и 60г свинца

15%

65%

30%

15%

65%

30%

и получили 600 г 15%-го раствора. Сколько граммов каждого

раствора надо было взять?

Решение 1: аналитическая модель. Обозначим x массу первого
раствора, тогда масса второго (600 - x). Составим уравнение:
30x + 10* (600 - x) = 600 *15 x = 150
Решение 2: с использованием графика.
Приравнивание площадей равновеликих прямоугольников:
15x = 5 (600- x)
x =150






Ответ: 150г 30% и 450г 10% раствора

5% и 40%. Сколько нужно взять металла каждого из

этих сортов, чтобы получить140 т стали с содержанием 30% никеля?

С использованием графика:
(приравнивание площадей
равновеликих
прямоугольников)
10*х = 25*(140 – х)
х = 100
140 – 100 = 40

Ответ: 100 т и 40 т

Взяли 0,5 л первого и 1,5 л второго раствора

и образовали новый раствор. Какова концентрация кислоты в новом растворе?

Так как первый раствор 20 % - й, то в нем 0,2 объема занимает «чистая» кислота. Так как объем первого раствора равен 0,5л, то в этом количестве содержится 0,2*0,5=0,1 л «чистой» кислоты.
Аналогично во втором растворе будет содержаться 0,3*1,5=0,45л «чистой» кислоты.
При смешивании растворов получим 0,5+1,5=2л кислотного раствора, в котором 0,1+0,45=0,55л «чистой» кислоты.
Отсюда следует, что концентрация кислоты в новом растворе есть отношение 0,55:2=0,275, т.е.27,5%.
Ответ: концентрация кислоты в новом растворе 27,5%

6% и 11%. Сколько «бедной» руды надо взять, чтобы

получить при смешивании с «богатой» 20 т руды с содержанием меди 8%?

Аналитическая модель:
Переведем проценты в дроби:
6%=0,06; 11%=0,11; 8%=0,08
Пусть надо взять х т «бедной» руды,
которая будет содержать 0,06х т меди,
а «богатой» руды надо взять (20-х) т,
которая будет содержать 0,11(20 - х) т
меди.
Так как получившиеся 20 т руды
будут содержать 20*0,08 т меди, то
получим уравнение:
0,06х + 0,11(20 - х) = 20*0,08.
Решив уравнение, получим х = 12.
Ответ: 12т руды с 6% содержанием меди

некоторого человека были на продажу масла двух сортов: одно

ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?


Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.

10

6

1

3

7

сортов –цейлонский по 5 гривен за фунт,
индийский по

8 гривен за фунт и китайский по 12 гривен за фунт.
В каких долях нужно смешать эти сорта, чтобы получить чай
стоимостью 6 гривен за фунт?





Взять 6+2=8 частей чая ценой по 5 гривен и по
одной части ценой 8 гривен и 12 гривен за один фунт.
Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и
по1/10 фунта чая ценой 8 и 12 гривен за фунт, то
получим 1 фунт чая ценой
8/10*5 + 1/10*8 + 1/10*12 = 6 гривен

6

5

12

6

1

6

5

8

1

2

6

2/8

1

1/10

150 г 864-й пробы. Определить пробу сплава.
Пусть

проба сплава равна х.
Составим диагональную схему:



Получаем:
(864 – х) : (х – 600) = 75 : 150
1728 – 2х = х – 600
х = 776.
Ответ: сплав 776-й пробы.

разных
концентраций используется «правило креста». В точке
пересечения двух

прямых обозначают концентрацию смеси.
У концов этих прямых слева от точки пересечения указывают
концентрации составных частей смеси, а справа – разности
концентраций смеси и ее составных частей:



Например, для приготовления 30 г 80%-го раствора H3PO4
требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты.

и 2 кг и с концентрацией меди 0,6 и

0,8 отрезали по куску равной массы. Каждый из отрезанных кусков сплавлен с остатком другого куска, после чего концентрация меди в обоих сплавах стала одинаковой. Какова масса каждого из отрезанных кусков?

Обозначим массу отрезанного куска х (кг).
Так как в обоих сплавах концентрация меди после двух операция
стала одинаковой, то массы сплавов и массы меди в этих сплавах
пропорциональны.
Первоначально массы меди в сплавах равны 0,6*3(кг) и 0,8*2(кг).
После того, как отрезали куски массой х(кг), содержание меди
стало 0,6(3-х) и 0,8(2-х), а после сплавления
0,6(3-х) + 0,8х и 0,8(2-х) +0,6х

= , х = 1,2
Ответ: 1,2 кг

1,8+0,2х

2

3

mм(кг)

mc(кг)

1,6-0,2х

содержит меди на 11 кг больше, чем цинка. Этот

кусок латуни сплавили с 12 кг меди и получили латунь, в котором 75% меди. Сколько килограммов меди было в куске латуни первоначально?

Обозначим искомую величину за х.
Тогда масса первоначального куска латуни 2х – 11, а его содержание меди составляет р = процентов.
Поскольку «медность» куска меди 100%, то по правилу квадрата получаем:
= , х = 22,5



Ответ: 22,5 кг меди было в куске латуни.

р

25

75

100

75 - р

6л молока шестипроцентной жирности. Сколько процентов составляет жирность молока

в бидоне?

Обозначим искомую величину за Х.
По правилу квадрата получим:



Составим пропорцию:
= , х = 4,8


Ответ: 4,8 % - жирность молока.

3

6 - х

х

6

х - 3

сплавы
1.Сплавили 2кг сплава цинка и меди, содержащего 20%
цинка, и

6кг сплава цинка и меди, содержащего 40%
цинка. Найдите процентную концентрацию меди в
получившемся сплаве. Ответ: 65% меди.
2. Для приготовления маринада необходим
2% раствор уксуса. Сколько нужно добавить
воды в 100г 9%-го раствора уксуса, чтобы получить
раствор для маринада? Ответ: 350 г воды