- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Основные законы алгебры логики
Содержание
- 2. Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия)
- 3. В основе современной логики лежат учения, созданные
- 4. ЛОГИКА – наука о формах и способах мышления
- 5. Законы мышления отражают в сознании человека свойства, связи и отношения объектов окружающего мира
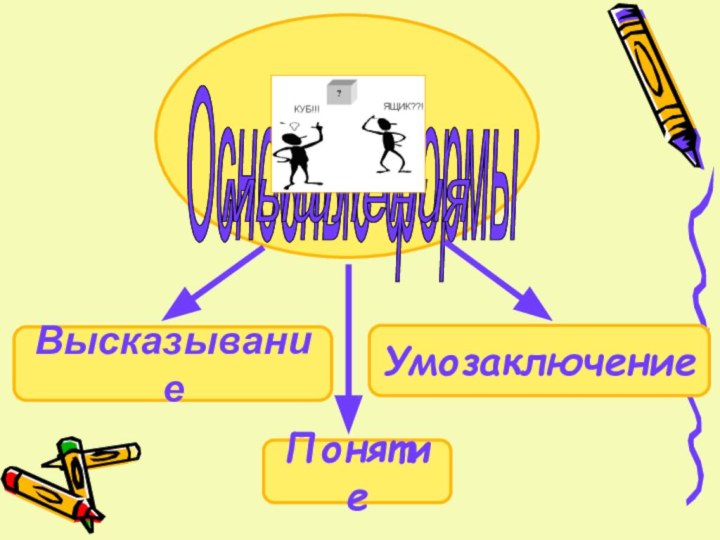
- 6. ВысказываниеПонятиеУмозаключение
- 7. Высказывание –логическое выражение, истинность которого требуется доказать
- 8. Высказывание не может быть выражено повелительным или вопросительным предложением
- 9. Высказывание имеет 2 значения:ложь – (false) – 0истина – (true) - 1
- 10. Высказывание – обозначается большими буквами латинского алфавита (А, В, С)
- 11. ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- 13. Таблица истинности логического умножения
- 14. Дизъюнкция (логическое сложение)читается обозначается А ν BДизъюнкция истинна, когда хотя бы одно высказывание истинноИЛИ
- 15. Таблица истинности логического сложения
- 16. Инверсия (логическое отрицание)читается обозначается А (не А)НЕ
- 17. Таблица истинности логического отрицания
- 18. Импликация (логическое следование)обозначается А BИмпликация ложна,
- 19. Таблица истинности логической функции «импликация»
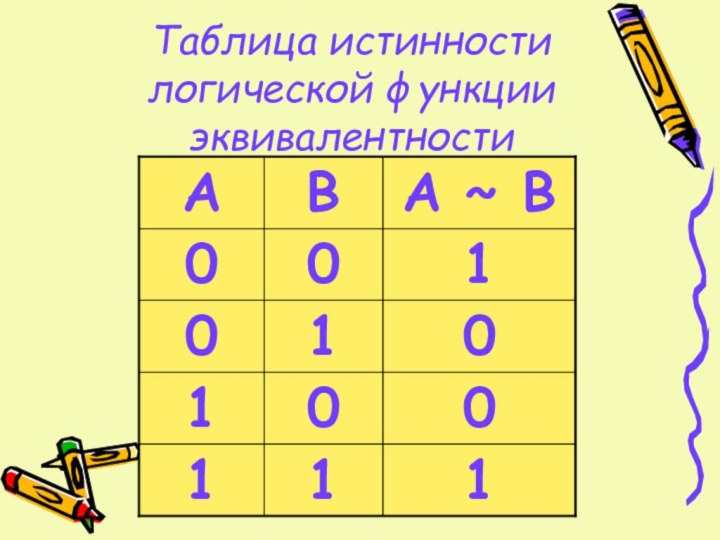
- 20. Эквивалентность (логическое равенство)обозначается А ~ BЭквивалентность
- 21. Таблица истинности логической функции эквивалентности
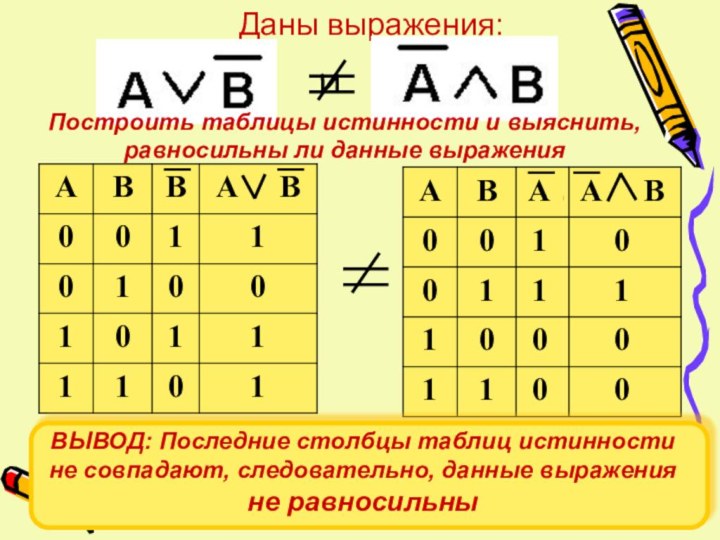
- 22. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными
- 23. Даны выражения: иПостроить таблицы истинности и выяснить, равносильны ли данные выражения
- 24. Скачать презентацию
- 25. Похожие презентации
Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия)





















Слайд 3
В основе современной
логики лежат учения,
созданные древнегреческими
мыслителями (Аристотель, Геродот)
Аристотель 384-322 до н.э
Геродот ок 490-425 до
н.э
Слайд 5
Законы мышления
отражают в
сознании человека свойства,
связи
и отношения объектов
окружающего мира
Слайд 14
Дизъюнкция
(логическое сложение)
читается
обозначается А ν B
Дизъюнкция истинна,
когда хотя бы одно
высказывание истинно
ИЛИ
Слайд 18
Импликация
(логическое следование)
обозначается А B
Импликация ложна,
тогда
и только тогда,
когда из истины следует
ложный вывод
Слайд 20
Эквивалентность
(логическое равенство)
обозначается А ~ B
Эквивалентность истинна,
тогда и только тогда,
когда оба высказывания
одновременно либо
ложны, либо истинны